Опуклі функції та їх застосування до доведення нерівностей

Нерівність Єнсена

Розглянемо функцію 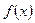, визначену та диференційовану на відрізку 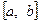і позначимо через 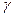частину її графіка, що відповідає відрізку .

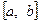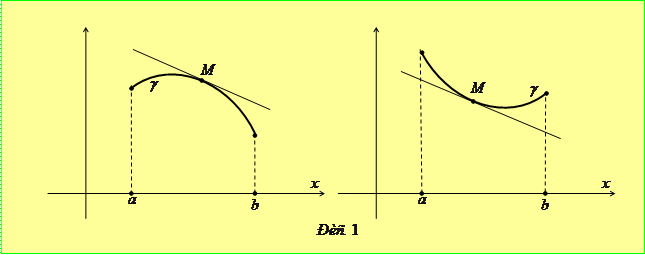Функцію називають опуклою вгору (вниз) на відрізку , якщо для довільної точки крива 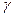лежить нижче (вище) від дотичної до 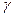, проведеної в точці 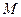(рис. 1).

Серед деяких властивостей опуклих функцій відмітимо ті, які в подальшому використаємо при доведенні деяких нерівностей.

1. Якщо функція 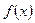на відрізку 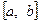опукла вгору, то для двох довільних різних точок 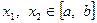виконується нерівність

.

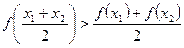2. Якщо функція 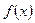на відрізку 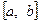опукла вниз, то для двох довільних різних точок 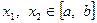виконується нерівність

.

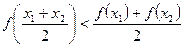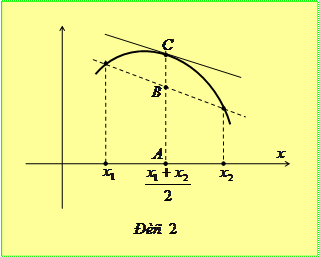Доведення обох тверджень очевидне. Зокрема у першому випадку достатньо побачити, що довжина відрізка 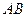, який дорівнює 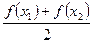, менша від довжини відрізка 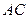, який дорівнює 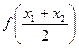(рис. 2).

3. Якщо функція 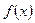на відрізку 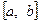опукла вгору і числа 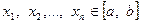не всі рівні між собою, то виконується нерівність

. (*)

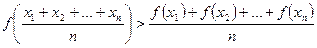4. Якщо функція 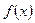на відрізку 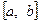опукла вниз і числа 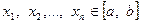не всі рівні між собою, то виконується нерівність

. (**)

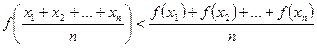Доведення двох останніх тверджень можна реалізувати за допомогою методу математичної індукції.

Нерівності (*), (**), які у математиці називають нерівностями Єнсена, можуть служити основою для складання та доведення різних нерівностей. Достатньо вибрати конкретну функцію, опуклу вгору або вниз та замінити нею функцію .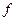

Наведемо приклади подібних доведень.

Задача 2.5.1. Довести, що для різних 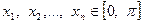виконується нерівність

.

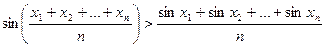Доведення. Для доведення достатньо у співвідношенні (*) використати замість 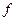функцію 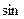, графік якої на вказаному відрізку опуклий вверх.

Задача 2.5.2. Довести, що для довільних чисел 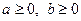виконується нерівність

.

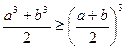Доведення. Тут ми повертаємося до розгляду задачі 1.3.2. У цьому випадку використовуємо співвідношення (**), а в ролі 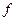функцію 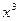, графік якої при 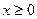опуклий вниз.

Задача 2.5.3. Порівняти числ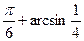а та .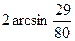

Доведення. Розглянемо функцію 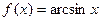, графік якої на проміжку 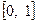опуклий вниз. Застосувавши нерівність Єнсена у виді співвідношення (**), отримуємо

.

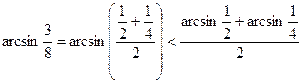Тому

.

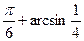
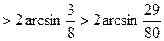Задача 2.5.4. Довести, що правильний 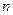-кутник має найбільший периметр серед усіх вписаних в коло 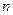-кутників.

Доведення. Нехай 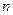-кутник 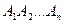вписаний у коло з центром у точці 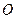та радіусом 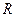. Позначимо 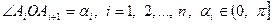. Тоді 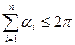(знак строгої нерівності буде у випадку, коли центр кола лежить поза многокутником). Користуючись теоремою косинусів отримуємо, що для периметра многокутника 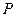маємо

.

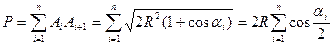Оскільки 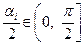і функція 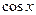на вказаній множині значень опукла вгору, то з нерівності Єнсена отримуємо, що

,

а саме останньому значенню дорівнює периметр правильного вписаного в коло многокутника.

Розглянемо, як нерівність Єнсена та наведені міркування можна використати для доведення класичних нерівностей між середніми. Як ми уже знаємо (розділ 1.7), для 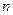додатних чисел 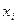такими є середнє арифметичне 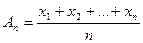, середнє геометричне 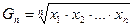, середнє квадратичне 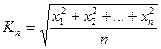та середнє гармонічне 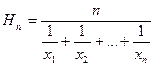. Ці середні величини знаходяться у співвідношеннях 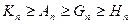. Знак рівності в усіх випадках виконується тоді і тільки тоді, коли 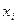рівні. Доведемо строгі нерівності, вважаючи 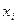різними.

Для доведення першої нерівності 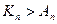, тобто

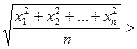
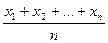
використаємо у ролі 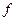функцію 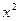, графік якої опуклий вниз, та співвідношення (**). Відповідно до нього отримуємо

,

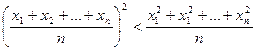звідки, добувши корінь з обох частин, дістаємо шукане співвідношення.

Для доведення другої нерівності 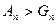, тобто

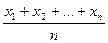
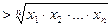
використаємо у ролі функцію 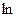, графік якої опуклий вгору, та співвідношення (*). Отримуємо

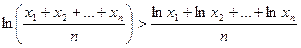
або

.

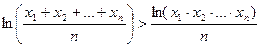Потенціюючи одержаний вираз, отримуємо шукане співвідношення.

Для доведення останньої нерівності 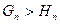, тобто нерівності між середнім геометричним та середнім гармонічним

,

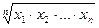
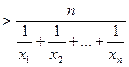знову використаємо функцію 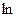, тільки співвідношення (*) застосуємо до чисел 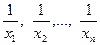. Отримуємо

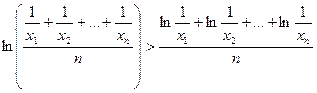
або

,

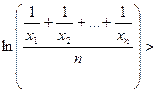
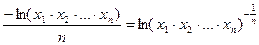що фактично завершує доведення потрібної нерівності.

Нерівність Юнга

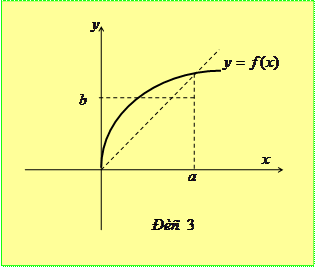Нехай 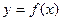– неперервна строго зростаюча функція від 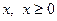, і 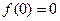(див. рис. 3). Розглядаючи площі, представлені відповідними інтегралами, ми переконуємося в тому, що

, (***)

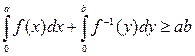де 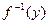- функція, обернена до 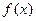. Легко бачити, що рівність тут має місце тільки при 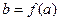. Ця нерівність називається нерівністю Юнга. Вибираючи у ролі 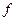різні функції, ми отримуємо ряд цікавих результатів.

Візьмемо, наприклад, у ролі функції 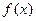функцію 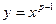, p>1, оберненою до якої є функція 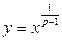. У цьому випадку співвідношення (***) приймає вид

,

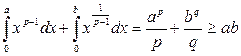де .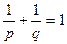

Нехай 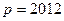і 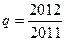. Тоді отримуємо, що при 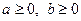виконується нерівність .

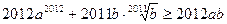Вибираючи в ролі функції 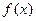функцію 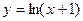та використовуючи обернену до неї функцію 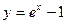із (***) знаходимо

.

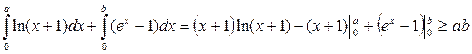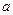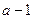Замінюючи на , отримуємо нерівність 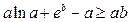. Одержане співвідношення в математиці застосовується в теорії рядів Фур’є.

Нехай 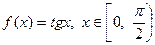. Тоді 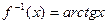. Користуючись нерівністю Юнга, знаходимо

,

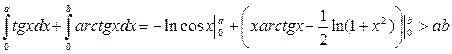звідки отримуємо нерівність

.

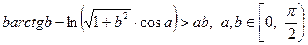При 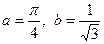дістаєм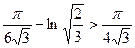о або .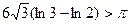

Таким чином, доведена нерівність 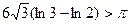.