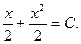Дифференциальные уравнения первого порядка. Постановка задачи Коши.

Рассмотрим дифференциальное уравнение первого порядка.

Общий вид уравнения первого порядка

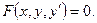
Если это уравнение разрешить относительно 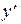, то есть

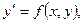(12)

то уравнение называется уравнением первого порядка, разрешенным относительно производной.

Определение 4.Общим решением дифференциального уравнения (12) называется дифференцируемая функция

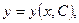(13)

которая зависит от одной произвольной постоянной С и обращает это уравнение в тождество.

Определение 5. Частным решением уравнения (12) называется решение, получаемое из общего решения (13) при каком-либо определенном значении произвольной постоянной С.

Рассмотрим дифференциальное уравнение первого порядка в симметричной относительно x и y форме:

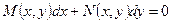(14)

При некоторых условиях уравнение (3) эквивалентно, по крайней мере, одному из дифференциальных уравнений вида:

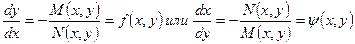
Дифференциальное уравнение 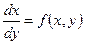определяет в каждой точке (x,y), где существует функция f(x,y), значение 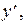то есть угловой коэффициент касательной к интегральной кривой в этой точке. Таким образом, дифференциальное уравнение (12) определяет поле направлений.

Задачи интегрирования дифференциального уравнения заключаются в том, чтобы найти интегральные кривые, направления касательных к которым в каждой точке совпадают с направлением поля. Для построения интегральных кривых используют метод изоклин.

Определение 6. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление.

Семейство изоклин дифференциального уравнения (12) определяется уравнением

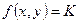, (15)

где K-параметр.

Постановка задачи Коши.

Задача о нахождении частного решения дифференциального уравнения, удовлетворяющего некоторым дополнительным условиям, часто встречается в приложениях. Если эти условия относятся к одному и тому же значению аргумента искомой функции, то их называют начальными. В том случае, когда начальные условия для дифференциального уравнения состоят в задании фиксированных значений функции и ее производных, их называют условиями Коши, а задачу – задачей Коши.

Задачей Коши для дифференциального уравнения (12) называют задачу нахождения решения 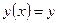уравнения 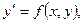удовлетворяющего начальному условию 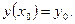(где 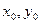- заданные числа, называемые начальными значениями или данными).

Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку 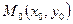плоскости XOY.

Теорема. (о существовании и единственности решений задачи Коши.)

(без доказательства)

Пусть функция 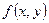и ее производные определены и непрерывны на открытом множестве 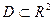. Тогда в некоторой окрестност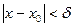и точки 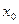существует непрерывное решение 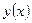задачи Коши:

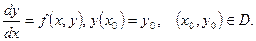
Замечание. Это решение единственно, т.е. если 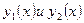- два непрерывных решения задачи Коши, то 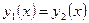для всех значений, при которых эти решения определены.

Как известно, общее решение уравнения (12) задается следующим равенством

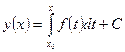(16)

Чтобы выделить частное решение уравнения (12), достаточно знать значение первообразной 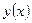в какой – либо точке. Пусть, например, 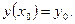Тогда из соотношения (16) имеем 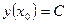или 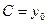, т. е. решение единственно и равно

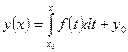(17)

Уравнение (17) называется частным решением задачи Коши.

Пример 3. Решить задачу Коши.

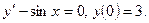
Решение. Согласно формуле (17) частное решение имеет вид

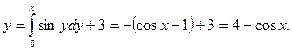
Классы дифференциальных уравнений, интегрируемых в квадратурах.

Определение 7. Дифференциальное уравнение первого порядка называется интегрируемым в квадратурах (или просто интегрируемым), если его общее решение может быть получено с помощью конечного числа алгебраических операций и квадратур.

Рассмотрим уравнение (14).

Определение 8. Уравнение (14) называется точным уравнением или уравнением в полных дифференциалах, если существует дифференцируемая функция 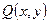, для которой левая часть уравнения (14) является полным дифференциалом, т.е.

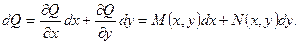
Пример 4. Для уравнения 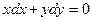общий интеграл записывается в виде 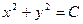(это легко проверить непосредственным дифференцированием). Очевидно, что интегральные линии, определяемые общим интегралом, являются концентрическими окружностями с центром в начале координат.

Теорема. Пусть функци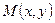и и 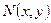непрерывно дифференцируемы на открытом множестве D. Для того чтобы уравнение (14) было точным необходимо, чтобы выполнялось условие

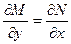(18)

Доказательство. Пусть уравнение (14) является точным. Тогда из определения точного уравнения и понятия полного дифференциала вытекает, что

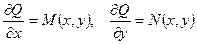(19)

Дифференцируя первое равенство по y, а второе – по x, имеем

.

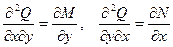Так как смешанные производные непрерывны, то они равны и, значит, справедливо условие (18). Что и требовалось доказать.

Пусть D – односвязная область. Покажем, что в этом случае условие (18) является достаточным. Проинтегрируем первое из равенств (19) по x, считая y постоянным:

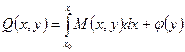, (20)

где 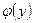- постоянная интегрирования, зависящая от y, а 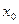- абсцисса любой точки из области единственности D. Подберем функцию 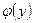так, чтобы выполнялось второе из равенств (19). Для этого продифференцируем равенство (20) по y, считая x постоянным:

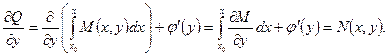
Откуда получим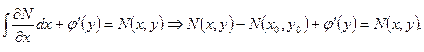

Следовательно, 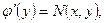т.е.

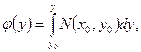(21)

где 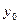- ордината произвольной точки из области единственности D, а произвольную постоянную считаем равной нулю. Из соотношений (20) и (21) получим

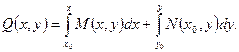
Итак, если в области D, не содержащей особых точек уравнения (12), выполнено условие (18), то общий интеграл уравнения выражается формулой

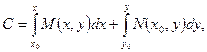(22)

где C – произвольная постоянная.

Пример 5. Решить уравнение .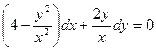

Решение. Обозначим 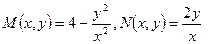и проверим выполнение условия (18): 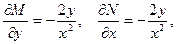т.е. 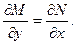Это уравнение в полных дифференциалах и его общий интеграл имеет вид (22), где 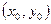- любая точка из области 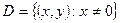. Положим, например, 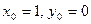, тогда

.

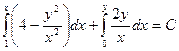Интегрируя, находим 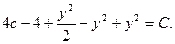Обозначив через 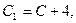получим общий интеграл исходного уравнения.

Интегрирующий множитель.

В том случае, когда условие (18) не выполняется, уравнение (14) не является уравнением в полных дифференциалах. Однако его можно проинтегрировать, если найти такую функцию 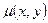, при умножении на которую всех членов уравнения оно становится точным:

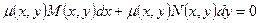(23)

Такая функция называется интегрирующим множителем уравнения (14). Общее решение уравнения (23) совпадает с общим решением уравнения (14).

Докажем, что для всякого уравнения (14), где M и N – непрерывно дифференцируемые функции, существует интегрирующий множитель. Пусть уравнение (14) не является точным. В силу теоремы существования и единственности решения, оно имеет общее решение в неявном виде. Дифференцируя это равенство по x, получим 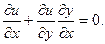Так как из уравнения (14) следует 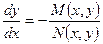, то 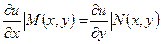. Обозначим через 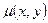общую величину этих двух равных отношений; тогда

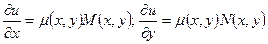(24)

Поскольку 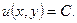есть общий интеграл уравнения (14), имеем 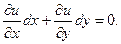Отсюда с учетом соотношения (24) получим уравнение вида (23), которое является точным. Следовательно, 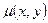- интегрирующий множитель уравнения.

Пример 6. Решить уравнение .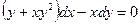

Решение. Проверим выполнение условия (18):

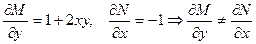, следовательно, это не уравнение в полных дифференциалах. Составим отношение

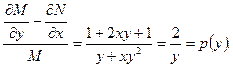
Найдем интегрирующий множитель

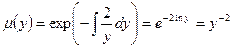
Тогда соответствующее точное уравнение будет иметь вид:

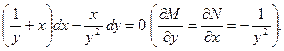
Область единственности этого уравнения е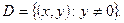сть Пусть 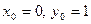. Находим общий интеграл

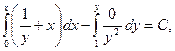
откуда, интегрируя, получим