Кинематический анализ кулачковых механизмов

Кулачковым механизмом называют механизм, состоящий из трех звеньев: стойки и кулачка с толкателем. Кулачок с толкателем образуют высшую кинематическую пару.

Толкатель является ведомым звеном, закон движения которого определяется профилем кулачка.

Кулачки и толкатели могут совершать вращательное и поступательное движения. Поступательно движущиеся кулачки и толкатели называют ползунами. Вращающиеся кулачки выполняют в виде дисковых, цилиндрических и коноидных конструкций. Толкатели, соверщающие колебательное движение, называют коромыслами. Независимо от вида движения толкатели могут иметь острые, сферические или плоские наконечники, контактирующие с профилем кулачка. В целях уменьшения износа поверхностей часто на наконечниках толкателей устанавливают ролик, заменяя трение скольжения трением качения.

Кулачковые механизмы предназначены для получения движений звеньев практически по любому заранее заданному закону. Их широко применяют в приборах, машинах, автоматических устройствах, роботах и манипуляторах.

Кулачковые механизмы, все точки звеньев которых совершают движение в одной плоскости или в параллельных плоскостях, называют плоскими.

Если точки звеньев перемещаются по пространственным траекториям, то кулачковые механизмы являются пространственными.

Изготовление коноидов для пространственных механизмов сложно и дорого, поэтому более широкое применение имеют плоские механизмы.

Комбинируя различные типы кулачков и толкателей, можно создать схемы механизмов, преобразующих движение:

- поступательное – в поступательное (рис. 67, а, б);

- поступательное – в колебательное (рис. 67, в, г);

- вращательное – в возвратно-поступательное (рис. 67, д, е, ж, м);

- вращательное – в колебательное (рис. 67, и, к, л, н);

- сложное движение двух независимых перменных в движение ведомого звена (поступательное или колебательное) (рис. 67, п, р).

Для прижатия толкателя к профилю кулачка используют силовое замыкание (с помощью пружин) или геометрическое замыкание (установка наконечника толкателя в пазах кулачка (рис. 67, л)).

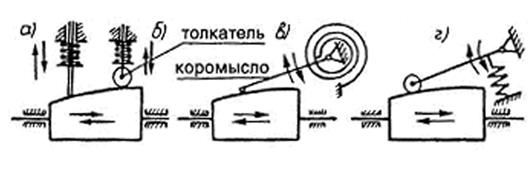
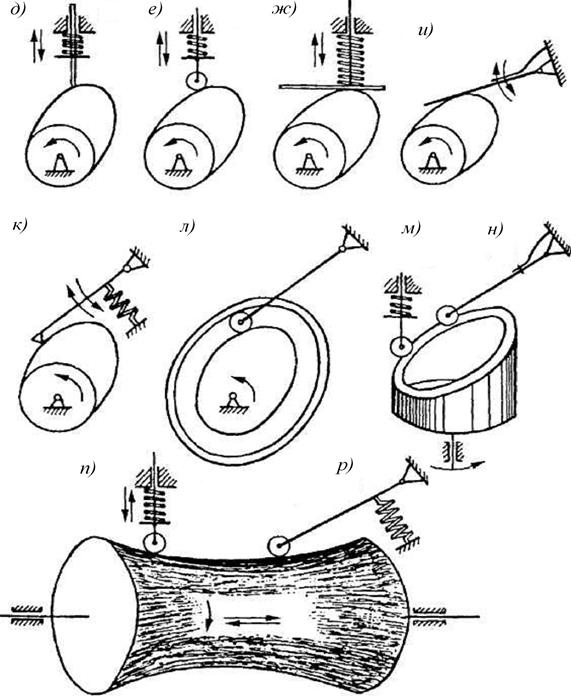
Рис. 67. Кулачковые механизмы

Если направление перемещения толкателя-ползуна проходит через центр вращения дискового кулачка, то механизм называют центральным.

Если направление перемещения толкателя расположено на некотором расстоянии от центра вращения кулачка, механизм является смещенным (или внеосным). Расстояние между линией движения толкателя и центром вращения кулачка называют эксцентриситетом.

Достоинства кулачковых механизмов:

- возможность воспроизведения практически любого закона движения выходного звена;

- малое количество деталей (кулачок и толкатель), что обеспечивает простоту сборки и обслуживания.

Недостатки:

- сложность изготовления;

- быстрый износ профиля кулачка, вызывающий изменение закона движения ведомого звена и снижение точности механизма.

При кинематическом исследовании считаются известными все размеры кулачкового механизма (длина коромысла, координаты точек, радиус ролика, координаты профиля и т. п.). Координаты профиля могут быть заданы в аналитическом (для простых профилей) или в графическом виде (чертеж или таблица точек). В результате кинематического исследования определится закон движения ведомого звена. Задача может быть решена как аналитически, так и графически. Аналитическое решение, как правило, используется в случаях, когда уравнение профиля кулачка задано в аналитическом виде (специальные кулачки).

Пример 1. В механизме с плоским толкателем (рис. 67, ж) кулачок выполнен в виде эксцентрика, то есть кругового цилиндра, вращающегося вокруг центра, смещенного на величину эксцентриситета e (рис. 68).

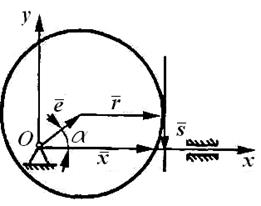
Рис. 68. Схема к примеру 1

Из уравнения замкнутости 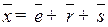получим закон перемещения толкателя в виде: .

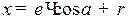Пример 2. Кулачок в механизме (рис. 67, д) выполнен по участкам архимедовой спирали согласно уравнению 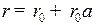(рис. 69), где r₀ – наименьший радиус-вектор его тела.

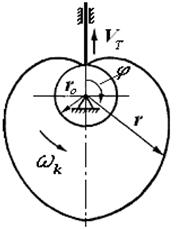
Рис. 69. Схема к примеру 2

В этом случае при повороте кулачка на угол 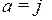толкатель переместится на величину 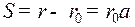. Передаточное отношение такого механизма на участке подъема 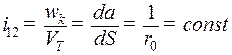, т. е. толкатель движется с постоянной скоростью.

При графическом решении задачи кинематического анализа после вычерчивания кулачкового механизма применяется метод обращения движения (инверсии): всему механизму сообщается дополнительное вращение с угловой скоростью .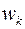

В такой системе отсчета кулачок неподвижен, а ведомое звено механизма совершает движение вокруг кулачка. Замеряя в нескольких положениях перемещения ведомого звена, можно построить график 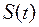или .

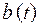Используя методы графического дифференцирования, можно получить график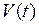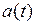и , или , .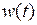

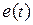Пример 3. Дан кулачковый механизм (рис. 67, л) с коромыслом. Известны: профиль кулачка, наименьший его радиус r₀, радиус ролика r_р, длина коромысла l, координаты точки О₁. Определить закон движения коромысла.

Вычерчиваем механизм в положении, когда (рис. 70) ролик касается наименьшего радиуса r₀ (OAk₁ = r₀ + r_р).

Размечаем окружность радиуса ОО₁ на несколько частей (обычно 12, 24
и более). Строим траекторию движения центра ролика А вокруг кулачка как кривую, соединяющую засечки радиуса r_р из точек профиля кулачка (рис. 70). Такая траектория иначе называется теоретическим профилем кулачка. Засечками из точек 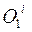радиусами О₁А получаем положения коромысла ( 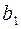, , 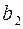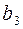) через равные промежутки времени.

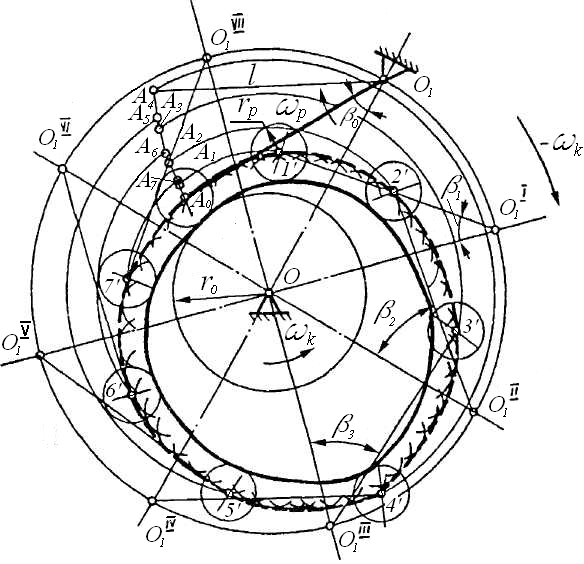
Рис. 70. Построение теоретического профиля кулачка

При этом между линией центров ОО₁ и коромыслом О₁А образуется некоторый начальный угол 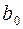. После сообщения системе угловой скорости – 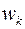коромысло начнет вращаться вокруг неподвижного кулачка.

Разности: ( 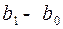), ( ), ( 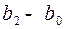), 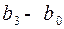… – дают угловые перемещения коромысла относительно его ближнего положения. По этим разностям строится график 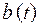или .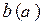

График угловой скорости коромысла 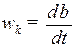или 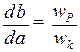строится графическим дифференцированием графика 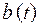или 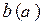. Известно, что производная с геометрической точки зрения является тангенсом угла наклона касательной в рассматриваемой точке. Так как проводить касательные к кривой весьма сложно, воспользуемся средними скоростями на участке между делениями.

Например, на участке 1–2: .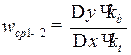

Из выбранной точки Р (рис. 71, б) проведем луч Р_т, параллельный хорде 1'2', до пересечения с осью ординат. Тогда

;

.

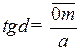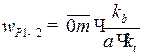Если принять 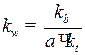, то отрезок 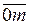выражает в масштабе 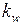скорость 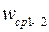, которую принято откладывать на середине участка 1–2 диаграммы. Проведя хорды на всех участках, а затем лучи из точки Р, им параллельные, получим в одном масштабе скорости средних точек участков и в целом диаграмму .

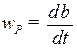Для диаграммы 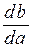имеем:

.

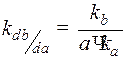Повторным дифференцированием получим диаграмму 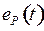или .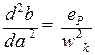

При этом: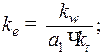

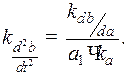
В общем виде ведомое звено (рис. 72) может иметь остановки при наибольшем удалении от центра кулачка (дальнее стояние 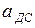) и при наименьшем удалении (ближнее стояние 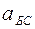). Между расстояниями ведомое звено движется, то удаляясь ( 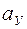), то приближаясь ( 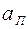)к центру кулачка. Обычно .

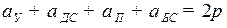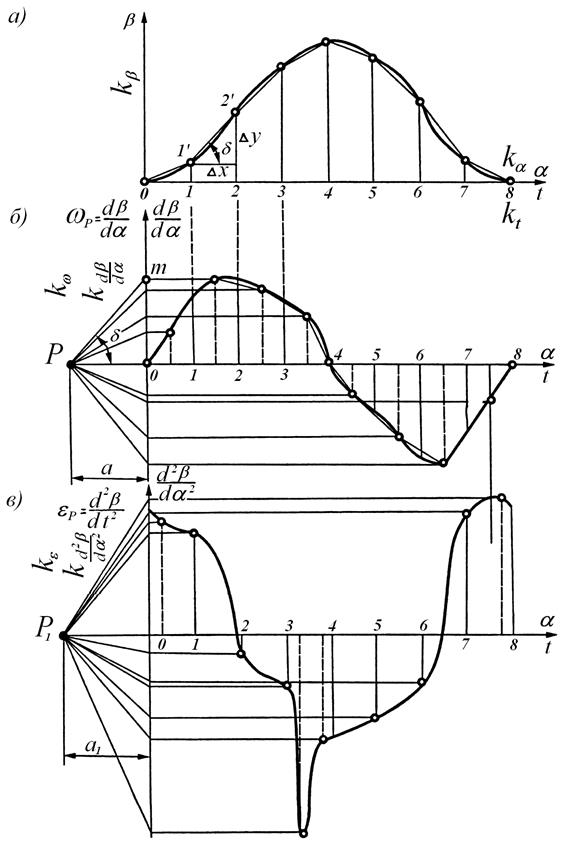
Рис. 71. Построение графиков перемещения, угловой скорости
и углового ускорения коромысла

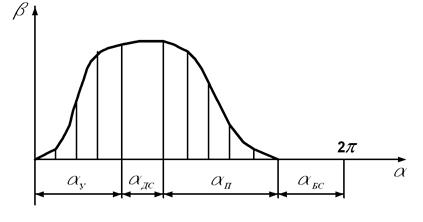
Рис. 72. График движения ведомого звена