Скалярное произведение в трехмерном пространстве
Скалярное произведение векторов
Угол между векторами; направляющие косинус векторы
Цели занятия:познакомиться с понятием эвклидова пространства; на основе предыдущей лекции рассмотреть эвклидово пространство как частный случай; понять смысл скалярного произведения; научиться определять скалярное произведение векторов, представленных в различных видах.
Роль и место лекции.
Полученные знания будут необходимы для восприятия темы «Векторный анализ, элементы теории поля». Такое фундаментальное понятие, как «скалярное произведение» позволит взглянуть на понятие пространства с другой стороны и осознать, что эвклидово пространство – это некоторая часть нашего мира, удовлетворяющая лишь определенным условиям. На основе этого пространства формируются аксиомы. В другом пространстве может формироваться новая математика.
1. Понятие «эвклидово пространство»
Возьмем трехмерное линейное пространство L= 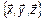 .
.
Определение 1.
Скалярным произведением двух элементов 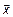 и
и 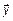 пространства L называется функционал
пространства L называется функционал 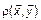 , удовлетворяющий определенным свойствам:
, удовлетворяющий определенным свойствам:
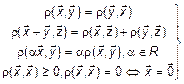 . (1).
. (1).
Обозначается скалярное произведение как 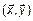 или
или 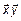 .
.
Возьмем n-мерное линейное пространство 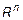 , в котором заданы два вектора
, в котором заданы два вектора 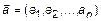 и
и 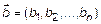 .
.
| |
Скалярным произведением векторов 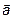 и
и 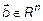 называется число, равное сумме попарных произведений соответствующих координат этих векторов.
называется число, равное сумме попарных произведений соответствующих координат этих векторов.
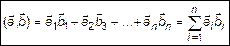 . (2)
. (2)
Проверим, удовлетворяет ли (2) определению 1.
1) 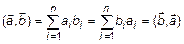 ;
;
2) 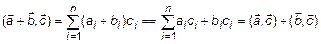 ;
;
3) 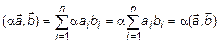 ;
;
4) 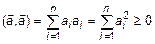 .
.
Аналогичным образом необходимо проверять любые функционалы, претендующие на скалярное произведение. Возьмем пространство 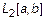 - квадрат интегрируемых функций
- квадрат интегрируемых функций
Определение 3.
Скалярным произведением функций 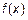 и
и 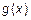
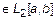 называется интеграл произведения этих функций на отрезке
называется интеграл произведения этих функций на отрезке 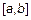
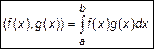 . (3)
. (3)
Удовлетворяет ли выражение (2) условиям (1) предлагается проверить самостоятельно.
Определение 4.
Пространство, в котором определено скалярное произведение, называется эвклидовым, т. е. 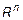 и
и 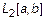 – эвклидовы.
– эвклидовы.
Теорема 1.
Всякое эвклидово пространство нормировано.
Доказательство.
Норма в эвклидовом пространстве задается как 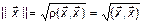
| |
1) 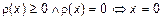 ;
;
2) 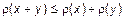 ;
;
3) 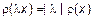 .
.
1. 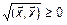 , следовательно,
, следовательно, 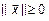 .
.
2. Для проверки второго условия воспользуемся неравенством Коши-Буняковского:
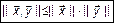 . (4)
. (4)
С учетом второго условия и (4) рассмотрим норму суммы:
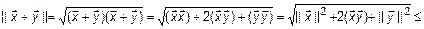
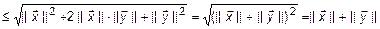 .
.
3. 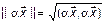 =
= 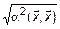 =
= 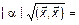
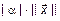 .
.
Все три условия выполняются. Теорема доказана.
2. Скалярное произведение в трехмерном пространстве
Возьмем два вектора 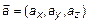 ,
, 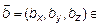
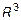 .
.
Определение 5.
Скалярным произведением векторов в 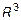 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:
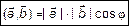 , где
, где 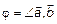 . (5)
. (5)
С учетом равенства 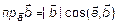 запишем выражение (5)
запишем выражение (5)
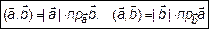 . (6)
. (6)
Покажем, что (5) также удовлетворяет условиям (1):
1) 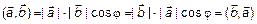 ;
;
2) 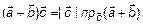 =(теорема 5, л. 2)=
=(теорема 5, л. 2)= 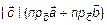 =
= 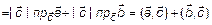 ;
;
3) 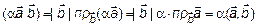 ;
;
4) 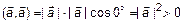
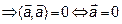 .
.
ПРИМЕР 1.
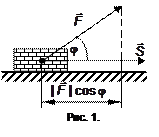
| |
 под углом
под углом  к поверхности прямолинейно
к поверхности прямолинейно 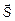 перемещено тело. При этом работа, выполненная силой, будет равна произведению длины пути на произведение модуля силы и косинуса угла
перемещено тело. При этом работа, выполненная силой, будет равна произведению длины пути на произведение модуля силы и косинуса угла 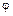 (рис. 1). Так как.
(рис. 1). Так как. 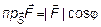 , то
, то 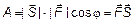 . Работа есть скалярное произведение векторов силы и пути.
. Работа есть скалярное произведение векторов силы и пути. Теорема 2.
Два вектора перпендикулярны 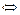 , когда их скалярное произведение было равно нулю.
, когда их скалярное произведение было равно нулю. 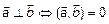 .
.
Доказательство.
Необходимость. Дано 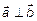 . Доказать, что
. Доказать, что 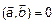 .
.
Из определения 5 следует, что 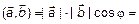 =
= 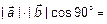
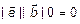 , следовательно,
, следовательно, 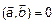 .
.
Достаточность. Дано 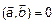 . Доказать, что
. Доказать, что 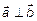 .
.
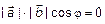 . Тогда
. Тогда 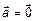 или
или 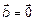 , или
, или 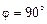 . Поскольку рассматриваем не нулевые векторы, то
. Поскольку рассматриваем не нулевые векторы, то 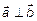 .
.
Вывод!!! 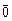 перпендикулярен любому вектору.
перпендикулярен любому вектору.
3. Скалярное произведение векторов
Возьмем два вектора в 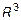 , заданных своими проекциями:
, заданных своими проекциями: 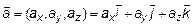 ,
, 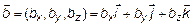 .
.
Скалярное произведение этих векторов
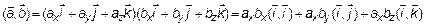
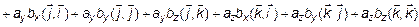
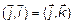
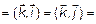
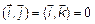 , т. к. это базисные векторы и
, т. к. это базисные векторы и 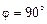 , а
, а 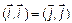
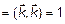 , так как
, так как 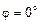 . Поэтому
. Поэтому
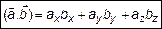 . (7)
. (7)
| |
Возьмем два вектора в 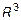 , заданных своими проекциями, –
, заданных своими проекциями, – 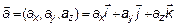 ,
, 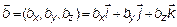 . Из (5)
. Из (5) 
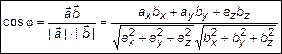 . (8)
. (8)
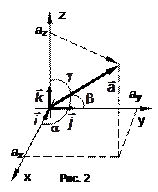 Найдем углы между вектором
Найдем углы между вектором 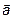 и базисными векторами
и базисными векторами 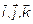 . То есть
. То есть 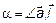 ,
, 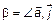 ,
, 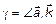 (рис. 2).
(рис. 2).
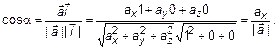 Аналогично найдем остальные косинусы
Аналогично найдем остальные косинусы
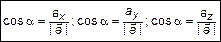 . (9)
. (9)
Определение 6.
Направляющим называется косинус угла между вектором и одним из базисных векторов. Единичный вектор может быть задан как 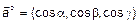 .
.
Заключение
В лекции рассматривалось эвклидово пространство, математический и физический смысл скалярного произведения; изучено понятие «направляющий косинус». Отметим:
- в эвклидовом пространстве пространство должно быть задано скалярное произведение;
- скалярное произведение есть число;
- два вектора перпендикулярны, если их скалярное произведение равно 0;
- угол между векторами определяется их скалярным произведением и длинами векторов;
- единичный вектор можно задавать направляющими косинусами.
Литература
1. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.
2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
| |
Определители, векторные и
