Зависимость двух случайных величин. Коэффициент корреляции

Характеристикой зависимости между случайными вели­чинами x и h служит математическое ожидание произведения отклонений x и h от их центров распределений (матема­тических ожиданий случайнйх величин), которое называется коэффициентом ковариации или просто ковариацией.

cov(x; h) = M((x–Mx)(h–Mh)).

Пусть x = {x₁, x₂, x₃,¼, x_n}, h = {y₁, y₂, y₃,¼,y_n}. Тогда

cov(x;h)= 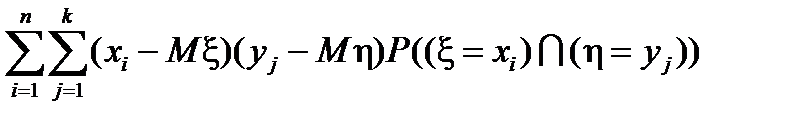(4)

Эту формулу можно интерпретировать так. Если при больших значениях x более вероятны большие значения h, а при малых значениях x более вероятны малые значения h, то в правой части формулы (4) положительные слагаемые доми­нируют, и ковариация принимает положительные значения.

Если же более вероятны произведения (x_i – Mx)(y_j – Mh), состоящие из сомножителей разного знака, то есть исходы случайного эксперимента, приводящие к большим значениям x в основном приводят к малым значениям h и наоборот, то ковариация принимает большие по модулю отрицательные значения.

В первом случае принято говорить о прямой связи: с рос­том x случайная величина h имеет тенденцию к возрастанию.

Во втором случае говорят об обратной связи: с ростом x случайная величина h имеет тенденцию к уменьшению или падению.

Ковариацию удобно представлять в виде:

cov(x; h)=M(xh)–MxMh.

Ковариация двух случайных величин равна математиче­скому ожиданию их произведения минус произведение мате­матических ожиданий.

Для независимых случайных величин x и h cov(x;h)=0.

Этому свойству можно придать более практическую формулировку: еслиcov(x;h)¹0, то случайные величины x и h зависимы.

Итак, ненулевая ковариация свидетельствует о зависимо­сти случайных величин.

Обратное утверждение не верно. Можно привести при­меры как независимых, так и зависимых случайных величин, ковариация между которыми равна нулю.

Величина cov(x;h) зависит от единиц измерения, в которых выражаются x и h. Поэтому cov(x;h) неудобно принимать за показатель связи. Чтобы иметь дело с безразмерным показателем, ковариацию делят на произведение среднеквадратических отклонений (СКО) x и h:

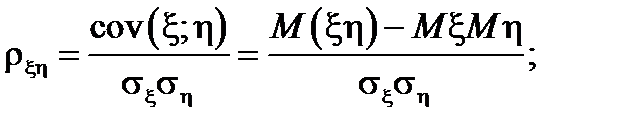
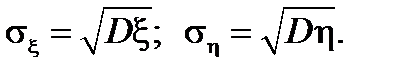
Полученное число r_xh называется коэффициентом корреляции случайных величин x и h.

Для независимых x и h r_xh=0 (так как в этом случае cov(x;h)=0).

Обратного заключения сделать нельзя. Случайные величины могут быть связаны даже функциональной зависимостью, но коэффициент их корреляции будет равен нулю.

Свойства коэффициента корреляции:

1) –1£r_xh£1;

2) Если r_xh=1, то h=kx+b, где k и b – константы, k>0.

3) Если r_xh=–1, то h=kx+b,где k<0.

4) Если h=kx+b, (k¹0) или x=k₁h+b₁, то r_xh=1 при k>0 или r_xh=–1 при k<0.

Коэффициент корреляции r_xh достигает своих предельных значений –1 и 1 в том и только в том случае, если совместное распределение x и h все концентрируется на некоторой прямой в плоскости x; h. Если êr_xhê<1, то линейной зависимости между x и h нет. Все же по мере приближения êr_xhê к единице величину êr_xhê можно считать мерой близости к полной линейной зависимости между x и h.

Как правило, говоря о корреляционной зависимости, име­ют в виду линейную корреляционную зависимость. Если имеется в виду нелинейная корреляционная зависимость, то это особо оговаривают

Можно говорить о совместном распределении двух непрерывных случайных величин.

В большинстве случаев возможен переход от непрерывных случайных величин к совместному распределению двух дискретных случайных величин следующим образом.

Нужно разбить отрезок [a; b] изменения случайной величи­ны x на равные отрезки [c₀=a; c₁]; [c₁; c₂]; [c₂; c₃], ¼ , [c_n–1; c_n=b]. За значение случайной величины x принять середину каждого отрезка.

Так же надо поступить со случайной величиной h, разбив ее область значений [e; f] на равные отрезки [g₀=e; g₁]; [g₁; g₂], … , [g_k–1; g_k=f], и приняв за возможные значения h середины отрезков [g_k–1; g_k].

Таким образом мы получили дискретные случайные величины x*={x₁; x₂; …x_n} и h*={y₁; y₂; …y_k}, причем каждой паре (x_i; y_j) ставится в соответствие вероятность

P_i^j = P((xÎ[c_i–1; c_i])∩(hÎ[g_j–1; g_j])).