В интегральной и дифференциальной форме

Участок цепи однородный, если на нём не действует ЭДС.

Ом экспериментально установил, что сила тока текущего по проводнику пропорциональна разности потенциалов на его концах. I=G*U

G – коэффициент пропорциональности который называется проводимость проводника. [G]= А/B = Си (Сименс)

Величина R = 1/G – обратная проводимости сопротивления проводника. [R] = B/A = Ом

Тогда закон Ома: 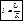- закон Ома в интегральной (общей) форме.

Для проводников с постоянным сечением сопротивление равно: 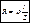l-длина;

S – площадь сечения; 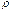- «ро» удельное сопротивление.

Заменим в законе Ома: I = j*S; U=E*l; .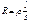

Получим: 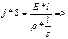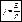- закон Ома в дифференциальной (частной) форме.

Величина 1/ 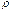= =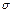> 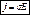или

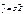
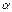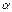Для металлов сопротивление пропорционально температуре: R=R₀(1+ t)=R₀ T

R₀ – сопротивление при t=0⁰C (T=273 K)

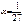- температурный коэффициент сопротивления.

При приближении к абсолютному нулю сопротивление металлов скачком падает до нуля – это явление сверхпроводимость.

Работа и мощность.

Закон Джоуля-Ленда в интегральной

И дифференциальной форме.

Из определения напряжения 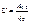следует, что работа по переносу заряда равна: А=U*q или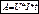

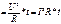
мощность тока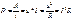

Если проводник не подвижен и нет химических превращений, то вся работа затрачивается на тепловыделение.

Следовательно: 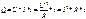- закон Джоуля-Ленса в интегральной форме.

Заменим: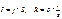

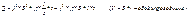
Введём удельную тепловую мощность:

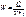- количество тепла выделяется в единицу объёма за единицу времени.

После подстановки получим:

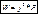- закон Джоуля – Ленса в дифференциальное форме. Если заменить: 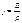, то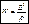

Закон Ома для участка цепи,

Содержащего ЭДС и для замкнутой цепи.

Участок цепи называется неоднородным если на нём действуют сторонние силы (ЭДС).

Полная работа по переносу заряда из точки 1 в точку 2 равна: А_1,2= q*E+q(φ₁- φ₂) (см § про ЭДС)

С другой стороны А= Q =I²(R+r)t = I(R+r)q

Приравняем: I(R+r)=E+(φ₁- φ₂) => 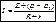- закон Ома для неоднородного участка цепи.

Если концы цепи замкнуты, то φ₁ = φ₂: 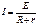- закон Ома для замкнутой цепи.

Законы (правила) Кирхгофа.

Узлом электрической цепи называется точка где сходится более двух проводников.

Правило1: Алгебраическая сумма токов сходящихся в узел равна нулю. 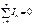(I₁+I₂+… +I_n = 0)

Рассмотрим замкнутый контур, выделенный из более сложной цепи.

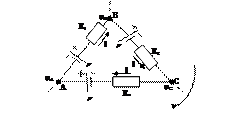
Укажем предположительно направление токов I₁,I₂,I₃.

Выберем направление обхода контура (например по часовой стрелке). Токи текущие по направлению обхода – положительные. ЭДС положительное если создаётся ток в направлении обхода. Применим к каждой ветви цепи закон Ома для неоднородного участка:

I₁R₁= (φ_A - φ_B) +E₁

-I₂R₂= (φ_B - φ_C) -E₂

I₃R₃=( φ_C - φ_A) +E₃

Сложим уравнения: I₁R₁-I₂R₂+I₃R₃ = E₁-E₂+E₃

Отсюда получим:

Правило 2: Сумма падения напряжений равна сумме ЭДС в любом замкнутом контуре.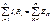

Собственная и примесная