Построение линий пересечения поверхностей

С помощью вспомогательных сферических поверхностей

Построение линий пересечения поверхностей с помощью вспомогательных секущих сфер можно двумя способами:

- способом концентрических сфер;

- способом эксцентрических сфер.

Рассмотрим первый способ построения линии пересечения. Этот способ применяется для построения линий пересечения двух поверхностей вращения, оси которых пересекаются. Для упрощения графического решения необходимо, чтобы плоскость, определяемая осями поверхности вращения, была параллельной какой-либо плоскости проекции.

Пример. Построить линию пересечения поверхности конуса Δ и цилиндрической поверхности Т с пересекающимися во фронтальной плоскости Ф (Ф₁) осями вращения i i′ (рисунок6.4). Заданные поверхности Δ и Т имеют общую фронтальную плоскость симметрии Ф (Ф₁). Следовательно, главные меридианы этих поверхностей пересекаются и дают в своем пересечении точки видимости линии пересечения на плоскости П₂ или самую высокую 1 и самую низкую 7 точки.

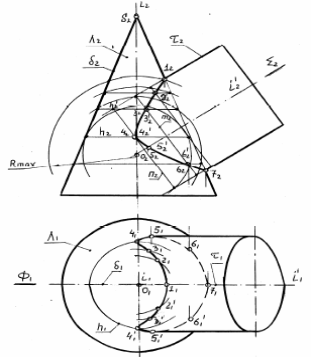
Рисунок 6.4

В данном примере выполнены условия, позволяющие применение вспомогательных секущих сфер для построения точек линии пересечения. Оси поверхностей вращения пересекаются в точке 0 (0₁; 0₂), которая является центром вспомогательных секущих сфер. Радиус сфер изменяется в пределах Rmin< R <Rmax. Радиус максимальной сферы определяется расстоянием от центра 0 до наиболее удаленной точки 1 (Rmax = 0₂1₂).

Радиус минимальной сферы определяется как радиус сферы, касающейся одной поверхности и пересекающей другую поверхность по окружности. В данном примере сфера радиуса R касается поверхности конуса по окружности h (h₂, h₁) и пересекает поверхность цилиндра по окружности n (n₁, n₂).

Плоскости этих окружностей перпендикулярны осям вращения поверхностей. В пересечении окружностей h и n отмечаем точки 4 и 4', принадлежащие линии пересечения поверхностей:

4₂(4′₂) = h₂∩n₂ ; 4₁(4′₁)=4₂ 4₁∩h₁.

Промежуточная сфера радиуса R пересекает поверхности Δ и Т по окружностям h′₁ и m , в пересечении которых определяются точки 3 и 3'. 3₂(3′₂) = h′₂∩m₂; 3₁(3′₁)=3₂ 3₁∩h₁. Аналогично определены точки 6 (6') и 2 (2′).

Определим видимость точек линии пересечения на плоскости проекций П₂.

Плоскостью видимости является плоскость Ф. Она делит кривую на две симметричные части, которые на П₂ совпадают. Видимая часть линии пересечения 1, 2′, 3′, 4′, 5′, 6′, 7- закрывает невидимую 1, 2, 3, 4, 5, 6, 7. На плоскости П₂ изображаем видимую часть кривой сплошной основной линией. Границы видимости - точки 1 и 7.

Видимость на плоскости проекций П₁ определяет поверхность цилиндра. Плоскость Σ (Σ₂) делит поверхность цилиндра на две части. Та часть поверхности цилиндра, которая расположена над плоскостью Σ, на плоскости П₁ видима, а значит и точки 4, 3, 2, 1, 2′, 3′,4′ видимы, как ей принадлежащие. Границы видимости точки 5 и 5'. Точки 5₁, 6₁, 7₁, 6'₁,5'₁ соединяем линией невидимого контура. Соединяя одноименные проекции построенных точек с учетом их видимости, получаем проекции линии пересечения поверхностей.