Линейные дифференциальные уравнения в частных производных. Линейные однородные дифференциальные уравнения в частных производных
Определение:Если в уравнении с частными производными первого порядка
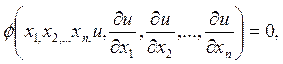 (1)
(1)
где 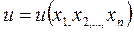 – искомая функция от независимых переменных
– искомая функция от независимых переменных 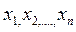 ;
; 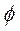 (∙) – известная функция своих аргументов, частные производные от искомой функции входят линейно, то такое уравнение называется линейным.
(∙) – известная функция своих аргументов, частные производные от искомой функции входят линейно, то такое уравнение называется линейным.
Следовательно, линейное уравнение можно записать так:
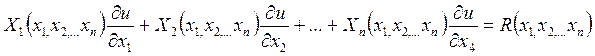 (2)
(2)
В случае, когда первая часть 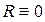 и коэффициенты
и коэффициенты 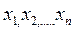 не зависят от переменной u (т.е. от искомой функции), линейное уравнение (2) принимает вид
не зависят от переменной u (т.е. от искомой функции), линейное уравнение (2) принимает вид
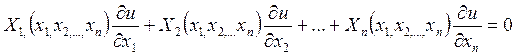 (3)
(3)
Определение:Линейное уравнение вида
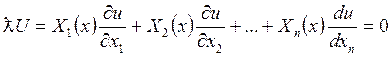 ,
,
где 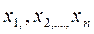 – заданные в области D непрерывно дифференцируемые функции независимых переменных
– заданные в области D непрерывно дифференцируемые функции независимых переменных 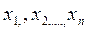 , не обращаются одновременно в нуль, т.е. при любом
, не обращаются одновременно в нуль, т.е. при любом 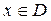
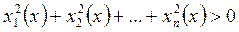 , называется линейным однородным уравнениемв частных производных первого порядка.
, называется линейным однородным уравнениемв частных производных первого порядка.
Так, уравнение 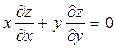 , линейное однородное дифференциальное уравнение в частных производных, где z – неизвестная функция от x и y, а уравнения
, линейное однородное дифференциальное уравнение в частных производных, где z – неизвестная функция от x и y, а уравнения 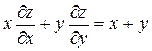 – линейное неоднородное ДУ в частных производных и
– линейное неоднородное ДУ в частных производных и 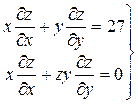 квазилинейное ДУ в ч.п. – линейные неоднородные.
квазилинейное ДУ в ч.п. – линейные неоднородные.
Определение: Решение в области 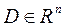 ДУ в частных производных (3) называется любая функция
ДУ в частных производных (3) называется любая функция 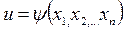 , непрерывная вместе со своими частными производными первого порядкаи образующая его в тождество по независимым переменным
, непрерывная вместе со своими частными производными первого порядкаи образующая его в тождество по независимым переменным 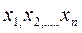 .
.
Геометрически решение 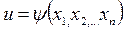 ДУ в частных производных можно интегрировать как поверхность в пространстве
ДУ в частных производных можно интегрировать как поверхность в пространстве 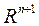 переменных
переменных 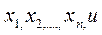 . Эту поверхность называют интегральной поверхностью.
. Эту поверхность называют интегральной поверхностью.
Рассмотрим вопрос о нахождении решений уравнений (3), определенных в некоторой окрестности точки 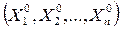 которые обращают уравнение (3) в тождество.
которые обращают уравнение (3) в тождество.
Заметим, прежде всего, что однородное уравнение (3) всегда имеет решение вида 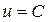 , где С=const. Такие решения будем называть тривиальными.
, где С=const. Такие решения будем называть тривиальными.
Покажем, что при сделанных предположениях относительно коэффициентов уравнения (3) оно имеет бесконечное множество нетривиальныхрешений.
Наряду с ДУ в частных производных (3) рассмотрим систему обыкновенных ДУ соответствующих этому уравнению
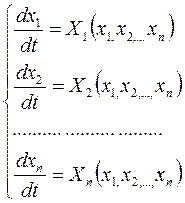
или в симметрической форме
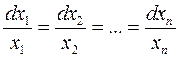 (5)
(5)
Система обыкновенных ДУ (4) называются системой уравнений характеристик для ДУ в частных производных (3), а ее интегральные кривые – характеристиками уравнения (3).
Теорема.
1. Если функция 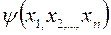 есть непрерывно дифференцируемый интеграл системы (5), то
есть непрерывно дифференцируемый интеграл системы (5), то 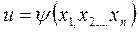 является решением уравнения (3);
является решением уравнения (3);
2. Если 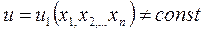 – решение уравнения (3), то
– решение уравнения (3), то 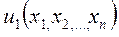 интеграл системы (5).
интеграл системы (5).
Доказательство: см. Н.М. Матвеев «Дифференциальные уравнения».
Из сформулированной теоремы вытекает, что задача интегрирования уравнения (3) и системы (5) равносильны.
При сделанных предположениях имеет ровно n-1 независимых интегралов
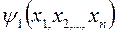 ,
, 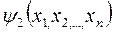 , …,
, …, 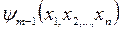 (6)
(6)
определенных и непрерывно дифференцируемых в некоторой окрестности начальной точки 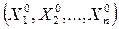 , т.к. при этих предположениях система (5) равносильна нормальной системе
, т.к. при этих предположениях система (5) равносильна нормальной системе 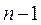 уравнений
уравнений
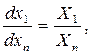
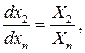 …,
…, 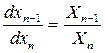 , (7)
, (7)
правые части которых определены и непрерывно дифференцируемы в некоторой окрестности точки 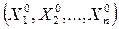 , а тогда система (7) имеет ровно
, а тогда система (7) имеет ровно 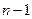 независимых интегралов, непрерывно дифференцируемые в некоторой окрестности этой точки.
независимых интегралов, непрерывно дифференцируемые в некоторой окрестности этой точки.
Любая непрерывно дифференцируемая функция от интегралов (6).
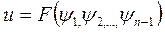 (8)
(8)
также будет интегралом системы (5) и, следовательно, решением уравнения (3)
Решение (8), где F – производная непрерывно дифференцируемая функция от своих аргументов, будем называть общим решением уравнения (3).
Рассмотрим случай двух независимых переменных в виде:
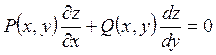 (9)
(9)
где 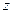 - неизвестная функция от x и
- неизвестная функция от x и 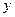 , а
, а 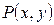 и
и 
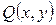 - заданные функции от x и
- заданные функции от x и 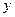 .
.
Каждому решению уравнения (9) соответствует в пространстве 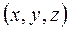 некоторая поверхность – интегральная поверхность уравнения (3).
некоторая поверхность – интегральная поверхность уравнения (3).
В рассматриваемом случае система (5) вырождается в одно уравнение
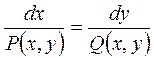 (10).
(10).
Пусть 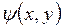 - интеграл этого уравнения. Тогда общим решением уравнения (9) будет
- интеграл этого уравнения. Тогда общим решением уравнения (9) будет
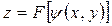 , (11)
, (11)
где F - произвольная непрерывно дифференцирующая функция.
Геометрически общему решению (11) соответствует семейство интегральных поверхностей, зависящее от произвольной функции F.
Примеры:
1) Решить уравнение 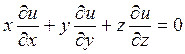
Решение:
Составим соответствующую ему систему дифференциальных уравнений в симметрической форме 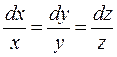 .
.
Решая ее, получим два независимых интеграла
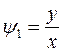 ,
, 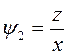 .
.
Поэтому общим решением исходного уравнения будет
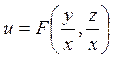 .
.
2) Решить уравнение: 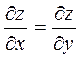
Решение:
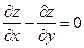
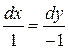
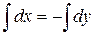
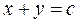
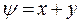
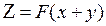
Задача Коши для уравнения с частными производными первого порядка (1) состоит в нахождении решения
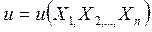 (12)
(12)
которое при фиксированном значении одной из независимых переменных, например 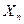 , обращается в заданную непрерывно дифференцируемую функцию от остальных переменных, т.е.
, обращается в заданную непрерывно дифференцируемую функцию от остальных переменных, т.е.
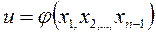 , при
, при 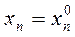 (13)
(13)
Условие (13) называется начальным условием решения (12).
В случае двух независимых переменных, т.е. для уравнения
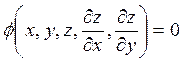 (14)
(14)
Задача Коши состоит в нахождении решения 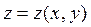 , удовлетворяющего начальному условию
, удовлетворяющего начальному условию 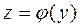 , при
, при 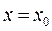 , т.е. ищется интегральная поверхность, которая проходит через заданную кривую
, т.е. ищется интегральная поверхность, которая проходит через заданную кривую 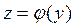 ,
, 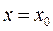 , лежащую в плоскости
, лежащую в плоскости 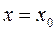 .
.
При постановке задачи Коши для однородного линейного уравнения (3), чтобы было обеспечено существование решения фиксируют значение той независимой переменной, для которой коэффициент при соответствующей частной производной от искомой функции отличен от нуля в начальной точке (х10, х20, …, хn0). В нашем случае нужно фиксировать хn.
Итак, будем искать решение уравнения (3), удовлетворяющее начальному условию (13). Для этого воспользуемся независимыми интегральными (6) системами (5). Положим в них xn=xn0 и обозначим полученные функции через 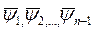 :
:
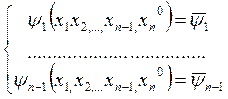 (15)
(15)
система (15) разрешима относительно 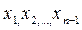 в некоторой окрестности начальной точки
в некоторой окрестности начальной точки 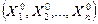 .
.
Найдем
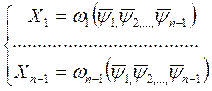 (16)
(16)
Построим функцию
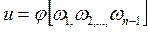 (17).
(17).
Эта функция и является искомым решением поставленной задачи Коши.
В случае двух независимых переменных получаем
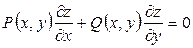
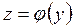 , при
, при 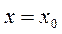
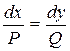 ,
, 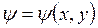
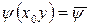 ,
, 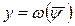
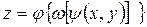
Примеры:
1. Решить уравнение: 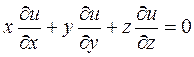 с условием
с условием 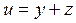 , при
, при 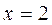 .
.
Решение: Здесь 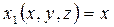 . Имеем
. Имеем 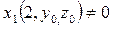 (какие бы значения
(какие бы значения 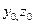 не взять), так что существование задачи Коши обеспечено.
не взять), так что существование задачи Коши обеспечено.
Находим первые интегралы
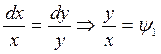
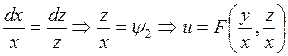 общее решение.
общее решение.
Полагая в первых интегралах 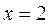 , получаем
, получаем 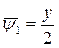 ,
, 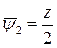 .
.
Откуда 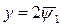 ,
, 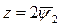 . Искомое решение будет
. Искомое решение будет
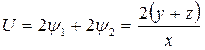 .
.
2. Найти интегральную поверхность уравнения 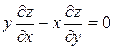 , проходящую через кривую
, проходящую через кривую 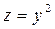 , при
, при 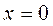 .
.
Решение: В начальном условии фиксировано значение 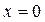 . Коэффициент отличен от нуля при
. Коэффициент отличен от нуля при 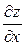 , т.к.
, т.к. 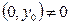 в любой точке, где
в любой точке, где 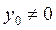 .
.
Такую точку и возьмем за начальную. В окрестности такой точки решение задачи Коши обеспечено. Напишем уравнение в симметрической форме
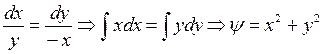
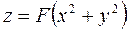 – общее решение.
– общее решение.
Полагаем в нем 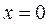 , находим
, находим 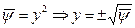
Искомым решением будет 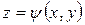 или
или 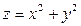
3. Проинтегрировать уравнение 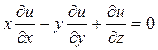 ,
, 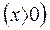 .
.
Найти интегральную поверхность, проходящую через кривую 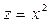 ,
, 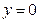 .
.
4. 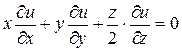 ,
, 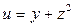 , при
, при 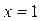
5. 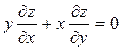 ,
, 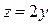 , при
, при 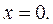 .
.
Лекция 3.
Линейные неоднородные дифференциальные уравнения в частных производных
Определение: Линейным неоднородным ДУ в частных производных первого порядка называют уравнение вида(1):
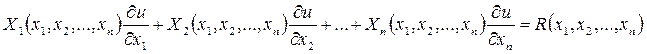
где 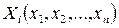 (
( 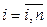 ) и
) и 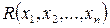 - заданные функции n независимых переменных х1,х2, …,хn , непрерывно дифференцируемых в некоторой области
- заданные функции n независимых переменных х1,х2, …,хn , непрерывно дифференцируемых в некоторой области 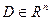 .
. 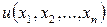 - искомая функция.
- искомая функция.
Определение: Решением ДУ в частных производных первого порядка (1) в области Д называют непрерывно дифференцируемую в области Д функцию 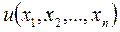 , которая обращает эти уравнения в тождество в любой точке
, которая обращает эти уравнения в тождество в любой точке 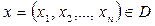 .
.
Предположим, что коэффициенты X1,X2, …,Xn и R определены и непрерывны вместе с частными производными в некоторой окрестности начальной точки 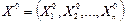 , причем
, причем 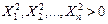 , то есть не все коэффициенты
, то есть не все коэффициенты
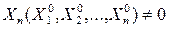 (2)
(2)
Будем искать решение уравнения (1) в неявном виде
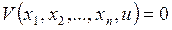 (3)
(3)
где V – некоторая непрерывно дифференцируемая функция своих аргументов, причем
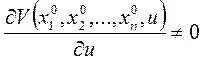 (4)
(4)
Продифференцируем соотношением (3) по хк , считая u функцией от х1,х2, …,хn, определяемой (согласно теореме о неявной функции) уравнением (4).
Находим
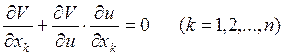 (5)
(5)
откуда
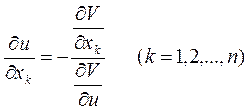 (6)
(6)
Подставляя (6) в (1), умножая на 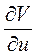 , перенося все члены в левую часть, получим
, перенося все члены в левую часть, получим
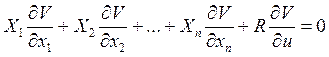 (7)
(7)
Уравнение (7) есть однородное линейное уравнение с искомой функцией V. Ему соответствуеющая характеристическая система в симметричной форме
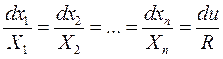 (8)
(8)
имеет n независимых интегралов
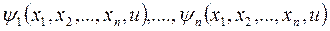 (9)
(9)
Поэтому линейные неоднородные ДУ в частных производных имеет общее решение вида
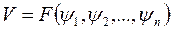 (10)
(10)
Подставляя (10) в (3), получим искомое решение уравнения (1) в виде
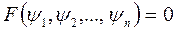 (11)
(11)
Это соотношение, где F – произвольная, непрерывно дифференцируемая функция, будем называть общим решением уравнения (1).
Если удается фактически разрешить (в элементарнах функциях) уравнение (11) относительно u, то получим общее решение в явном виде
u=f(x1, x2,..., xn) (12)
где f – произвольная непрерывно дифференцируемая функция.
В случае двух переменных имеем уравнение
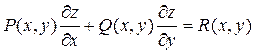 (13)
(13)
где z=z(x,y).
В симметрической форме примет вид:
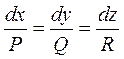 (14)
(14)
Если 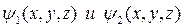 - независимые интегралы этой системы, то общее решение уравнения (13) имеет вид
- независимые интегралы этой системы, то общее решение уравнения (13) имеет вид 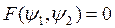 .
.
Примеры: Найти решение ДУ в частных производных.
1) 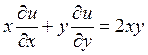
2) 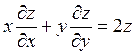
Решение:
1) Составим систему характеристических уравнений исходного ДУ в частных производных
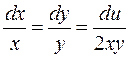
Отсюда найдем два независимых интегралов
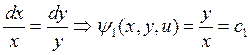 и
и 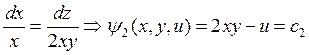 .
.
Тогда все решения ДУ в частных производных задаются формулой 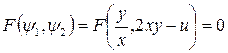 , где F – произвольная функция. Разрешая последнее равенство относительно 2-го аргумента, получим
, где F – произвольная функция. Разрешая последнее равенство относительно 2-го аргумента, получим 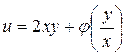 , где φ – непрерывно дифференцируемая функция.
, где φ – непрерывно дифференцируемая функция.
Задача Коши для неоднородного линейного уравнения (1) состоит в нахождении решения
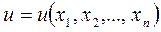 , (16)
, (16)
удовлетворяющего начальному условию
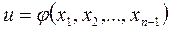 при
при 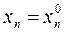 , (17)
, (17)
где φ – заданная непрерывно дифференцируемая функция.
Для решения задачи Коши воспользуемся независимыми интегралами (9) системы (8). Полагая в них 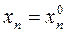 , получаем
, получаем
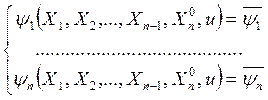 (18)
(18)
Разрешая эту систему относительно X1,X2, …,Xn-1, найдем
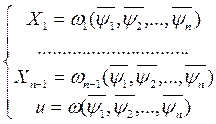 (19)
(19)
Подставляя эти значения X1,X2,…,Xn-1, в равенство 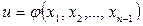 и заменяя
и заменяя 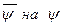 , получаем
, получаем
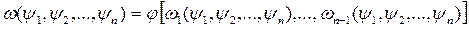 (20)
(20)
Это уравнение и определяет искомое решение (в неявном виде).
В случае двух независимых переменных имеем
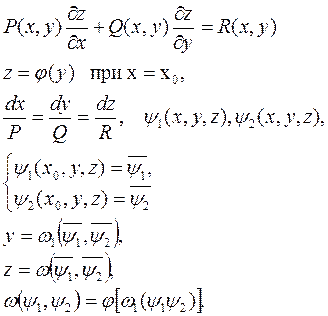
Примеры:
1) 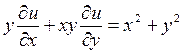
2) 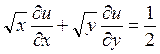
3) 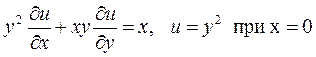
4) 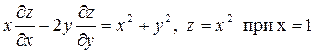
5) 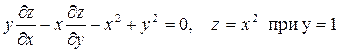
Найти решения линейного однородного ДУ в частных производных.
1) 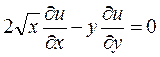
2) 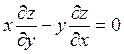
3) 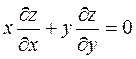
4) 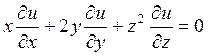
5) 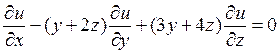
6) 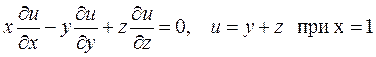
7) 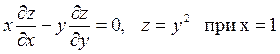
8) 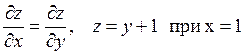
9) 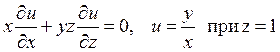
Лекция 4
Квазилинейные дифференциальные уравнения в частных производных первого порядка
Определение: Квазилинейным ДУ в частных производных первого порядка называют ДУ в частных производных вида:
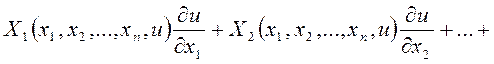
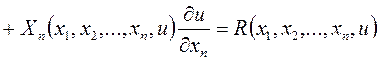 (1)
(1)
где 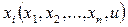 (
( 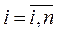 ) и
) и 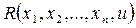 - заданные функции, непрерывно дифференцируемых в некоторой области
- заданные функции, непрерывно дифференцируемых в некоторой области 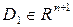 изменения n переменных
изменения n переменных 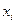 (
( 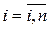 ) и искомой функции u.
) и искомой функции u.
Процесс нахождения общего решения квазилинейного ДУ в частных производных аналогичен нахождению общего решения линейного неоднородного ДУ в частных производных.
Основные этапы решения.
Система уравнений характеристик для квазилинейного ДУ в частных производных полностью совпадает с системой линейно- неоднородных ДУ в частных производных, то есть
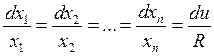 (2)
(2)
Пусть функции 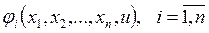 , являются в области
, являются в области 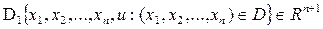 независимыми первыми интегралами системы (2)
независимыми первыми интегралами системы (2)
Интегральные кривые этой системы называют характеристиками квазилинейного ДУ в частных производных и общее решение можно получить из равенства
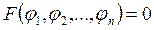 (3)
(3)
где F – произвольная непрерывно дифференцируемая функция.
Примеры:Найти общее решение уравнения
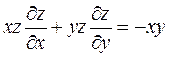
Решение: Составим систему характеристических уравнений исходного уравнения.
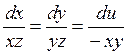
Отсюда найдем два независимых интегралов
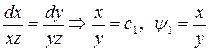 и
и 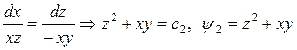 .
.
Тогда общее решение: 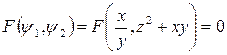 . Общий интеграл
. Общий интеграл 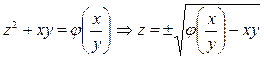 - общее решение.
- общее решение.
Постановка задачи Коши для квазилинейного ДУ в частных производных аналогична постановке этой задачи для линейного однородного ДУ в частных производных.
При практическом решение этой задачи необходимо руководствоваться следующими правилами:
Пусть решение 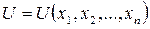 ДУ в частных производных (1) должно удовлетворять условию
ДУ в частных производных (1) должно удовлетворять условию 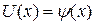 на поверхности S, которая задана условием
на поверхности S, которая задана условием 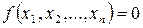 .
.
После нахождения характеристик 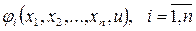 из системы уравнений характеристик
из системы уравнений характеристик 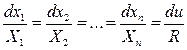 исключив из системы
исключив из системы
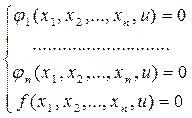
Переменные 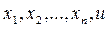 получим равенство
получим равенство 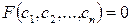 в котором следует поставить
в котором следует поставить 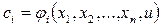 ,
, 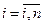 .
.
Тогда получим 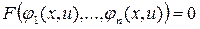 однако из решений
однако из решений 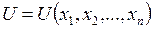 уравнения и будет искомая.
уравнения и будет искомая.
Примеры:
1. Найти общее решение уравнения
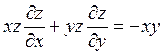
А так же интегральную поверхность, проходящую через кривую 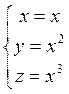
Решение: 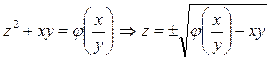 – общее решение (решение смотри выше).
– общее решение (решение смотри выше).
Найдем частное решение: вместо x, y, z подставим через параметр и получим 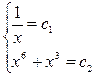 . Исключая х получим
. Исключая х получим 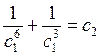 . Далее вместо с1 и с2 подставим и получим ответ:
. Далее вместо с1 и с2 подставим и получим ответ:
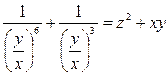 .
.
2. Найти общее решение уравнения 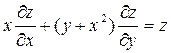 выделить решения, удовлетворяющее начальным условиям: z=y-x при x=2.
выделить решения, удовлетворяющее начальным условиям: z=y-x при x=2.
Решение: Составим систему характеристических уравнений исходного уравнения.
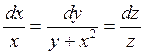
а) 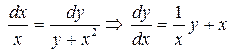 или
или 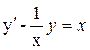 – линейное уравнение первого порядка
– линейное уравнение первого порядка
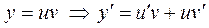
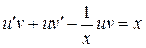
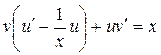
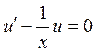
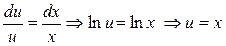
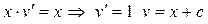
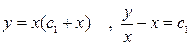
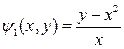
б) 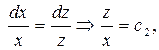
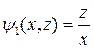
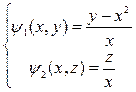
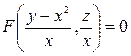 – общий интеграл
– общий интеграл
разделив относительно z, получим 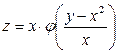 - общее решение.
- общее решение.
Найдем решение, удовлетворяющее начальным условиям
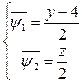
откуда
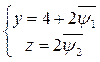
Подставляя эти значения y и z в формулу z=y-4 получим
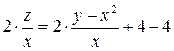
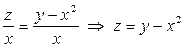 - частное решение.
- частное решение.
Это решение содержит в общим решении при 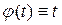
3. Найти общее решение уравнения 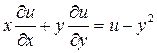 и выделить решения, удовлетворяющее начальным условиям: u =x-x2 при y=2.
и выделить решения, удовлетворяющее начальным условиям: u =x-x2 при y=2.
Решение:
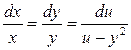
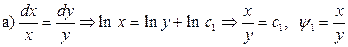
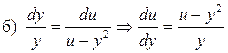
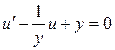
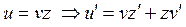
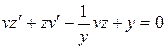
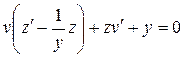
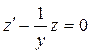
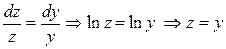
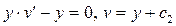
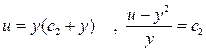
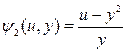
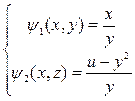
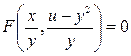 – общий интеграл
– общий интеграл
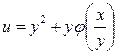 - общее решение.
- общее решение.
Используем начальные условия, получим
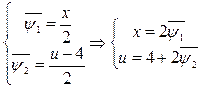
Подставляя эти значение x и u в формулу u=x-x2 получим
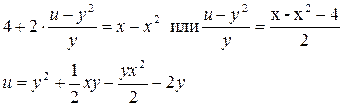
Примеры:
1. 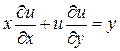
2. 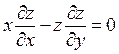
3. 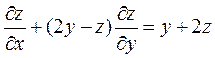
4. 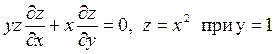
5. 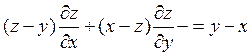
Лекция 5
Нелинейные дифференциальные уравнения в частных производных первого порядка
Рассмотрим нелинейное уравнение с частными производными первого порядка в случае двух независимых переменных.
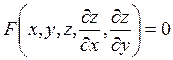 (1)
(1)
где z – искомая функция от x и y; 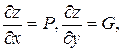 F – заданная непрерывно дифференцируемая функция своих аргументов в некоторой окрестности начальной точки
F – заданная непрерывно дифференцируемая функция своих аргументов в некоторой окрестности начальной точки 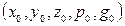 , зависящая от p и g нелинейно.
, зависящая от p и g нелинейно.
Оказывается, что задача интегрирование одного уравнение вида (1) является более трудной, чем интегрирование системы двух совместных уравнений такого вида, то есть имеющих решение, общее для обоих уравнений системы.
Рассмотрим систему
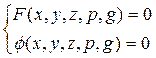 (2)
(2)
Предположим, что, разрешая её относительно от p и g, получим
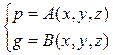 (3)
(3)
где A и B непрерывно дифференцируемы в некоторой окрестности начальной точки 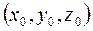 .
.
Найдем необходимое условие совместимости системы (3).
Предположим, что существует функции z=z(x,y), удовлетворяющая каждому уравнению этой системы и имеющая непрерывные частные производные 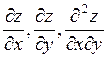 в некоторой окрестности начальной точке
в некоторой окрестности начальной точке 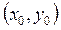 .
.
Дифференцируя уравнения (3) соответственно по у и по х, считая z=z(x,y) , получим
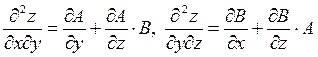 (4)
(4)
Отсюда следует (т.к. левые части 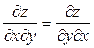 равны)
равны)
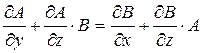 (5)
(5)
Условие (5) и есть необходимое условие совместимости системы (3).
Для того чтобы система (3) не только была совместна, но и существовало семейство решений, зависящее хоты бы от одной произвольной постоянной, необходимо, чтобы условие
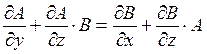 (6)
(6)
Выполнялось тождественно относительно x, y, z в рассматриваемой области.
Доказано, что тождественное выполнение условия (6) является и достаточно для существование такого семейство решений.
Если условие (6) выполняется тождественно относительно x, y, z, то оно называется условием полной интегрируемости системы (3).
Пример: Решить систему нелинейных ДУ в частных производных первого порядка
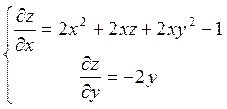
Решение: Сначала проверим необходимые и достаточные условие совместимости.
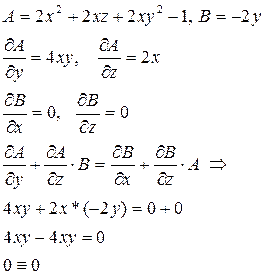
Условие выполняется, поэтому данная система вполне интегрируема (оно имеет семейство решение, зависящей от одной произвольной постоянной).
Первое уравнение 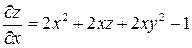 , если в нем фиксировать у, есть линейное уравнение относительно z.
, если в нем фиксировать у, есть линейное уравнение относительно z.
Интегрируя его, находим
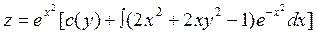
где С(у) – произвольная непрерывно дифференцируемая функция от у, так как
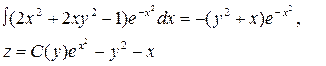
Выберем С(у) так, чтобы функция 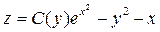 удовлетворяло и второму уравнению системы.
удовлетворяло и второму уравнению системы.
Дифференцируя z по у, получим 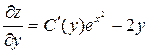 поэтому С(у) нужно определить из условия
поэтому С(у) нужно определить из условия 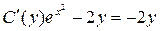 . Откуда
. Откуда 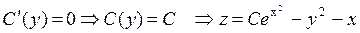 .
.
Рассмотрим решение уравнения Пфаффа.
Определение: Уравнением Пфаффаназывается уравнение вида
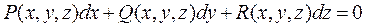 (7)
(7)
В этом уравнение все переменные x, y, z входят симметрично; и любую из них можно принять за искомую функцию.
Предположим, что коэффициент P, Q, R определены и непрерывны вместе с частными производными в окрестности начальной точки 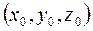 и не обращается в этой точке одновременно в нуль.
и не обращается в этой точке одновременно в нуль.
Пусть 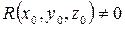 , тогда уравнение (7) можно переписать в следующем виде
, тогда уравнение (7) можно переписать в следующем виде
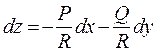 (8)
(8)
Найдем условие, при котором уравнение Пфаффа имеет семейство решений (интегральных поверхностей), зависящее от одной произвольной постоянной.
Так как на всякой интегральной поверхности z=z(x,y) должно выполнятся основное соотношение
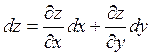 (9)
(9)
(аналогично 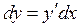 для случая обыкновенного дифференциального уравнения первого порядка), то для интегральных поверхностей имеем
для случая обыкновенного дифференциального уравнения первого порядка), то для интегральных поверхностей имеем
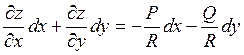 (10)
(10)
Отсюда,
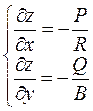 (11)
(11)
Уравнение Пфаффа (7) равносильно системе (11). Следовательно сводится к нахождению условия полной интегрируемости системы (11).
Так как 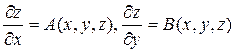
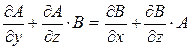 - условие полной интегрируемости, то записывая условие полной интегрируемости, получим
- условие полной интегрируемости, то записывая условие полной интегрируемости, получим
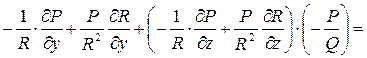
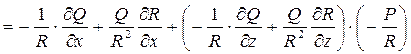
Умножая обе части на R2 и соберем члены при P, Q, R:
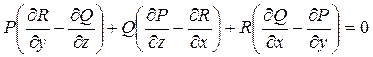 (*)
(*)
Для удобства запоминания можно записать в виде следующего равенства
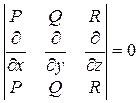 (**)
(**)
Если условие (**) выполняется тождественно, то оно называется условием полной интегрируемости уравнения Пфаффа.
Примеры.
1. Решить уравнение Пфаффа
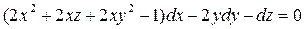
Решение: Проверяем условие полной интегрируемости
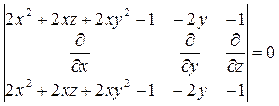
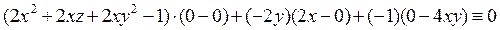
Следовательно, уравнение допускает семейство, интегральных поверхностей, зависящее от одной произвольной постоянной.
Принимая z за искомую функцию, запишем исходное уравнение системой
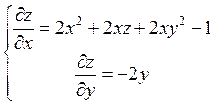
Эта система имеет семейство решений (смотрите выше) 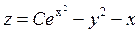 .
.
Метод Лагранжа – Шарни
Нахождение полного интеграла уравнения
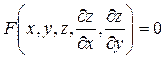 (1)
(1)
основано (по методу Лагранжа-Шарни) на нахождения другого уравнения 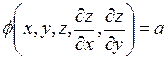 , где а – произвольная постоянная, чтобы полученная система уравнений
, где а – произвольная постоянная, чтобы полученная система уравнений
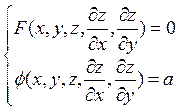 (2)
(2)
была разрешена относительно 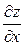 и
и 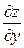 и чтобы в результате этого разрешения система
и чтобы в результате этого разрешения система
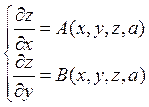 (3)
(3)
была вполне интегрируема.
Условием полной интегрируемости для системы (3) является
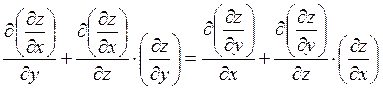
То есть 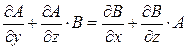
Затем решение выполняется известными методами.
Для нахождения функции 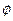 , введем для краткости обозначения
, введем для краткости обозначения
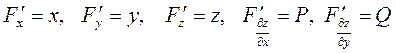
и из системы (3) приходим к уравнению
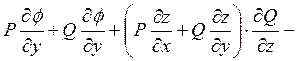
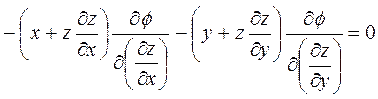 (4)
(4)
Это однородное ДУ в частных производных.
Составляем характеристическое уравнение в симметрической форме
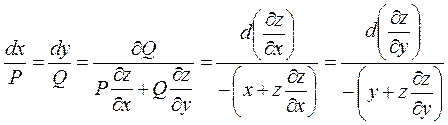 (5)
(5)
Отсюда находят только один первый интеграл системы виды 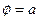 , где а – произвольная постоянная.
, где а – произвольная постоянная.
На практике сразу составляют систему (5), найдя её первый интеграл составляют систему (2). Затем переходят к системе (3) и проинтегрируют последнюю.
Пример.
1. 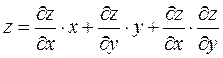
Решение:
Шаг 1:
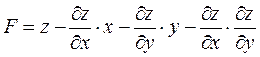
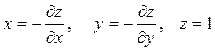
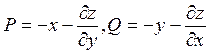
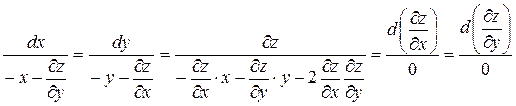
Шаг 2:
Решая, находим 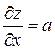 и переходим к системе
и переходим к системе
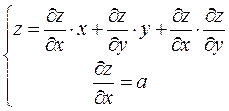
Разрешая относительно 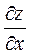 и
и 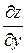 получим
получим
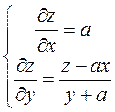
Эта система вполне интегрируема.
Решая её получим результат 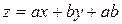 , где a и b – произвольные постоянные.
, где a и b – произвольные постоянные.
Примеры:
1. 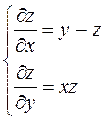
2. 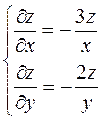
3. 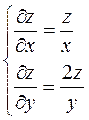
4. 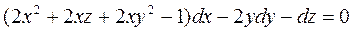
5. 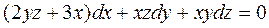
6. 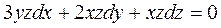
7. 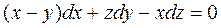
8. 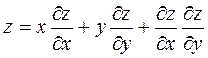
9.