Взаимное пересечение плоскостей общего положения

Задача Построить линию пересечения двух плоскостей общего положения.

Алгоритм решения задачиЛинию пересечения плоскостей строят по двум точкам, принадлежащим этой линии. Эти точки можно найти, дважды решив задачу на пересечение стороны одной плоскости с другой заданной плоскостью, используя вспомогательные секущие проецирующие плоскости. Проецирующие плоскости-посредники можно проводить через любые стороны плоскостей.

Способом конкурирующих точек определяется видимость сторон заданных плоскостей на каждой плоскости проекций (рисунок 8).

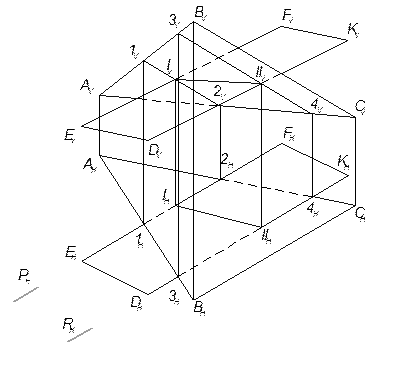
Рисунок 8 – Построение линии пересечения плоскостей

Пересечение поверхности с плоскостью

В сечении поверхности плоскостью получается плоская линия, которую строят по отдельным точкам. Сначала строят опорные точки, которые лежат на контурных линиях поверхности, а также точки на ребрах и линиях основания поверхности. Если проекции линии пересечения этими точками не определяются полностью, то строят дополнительные, промежуточные между опорными точки.

Задача Построить линию сечения многогранника горизонтально-проецирующей плоскостью.

Алгоритм решения задачиПри пересечении гранной поверхности с плоскостью в сечении получается многоугольник. Количество углов зависит от числа ребер, которые пересекает плоскостью. В точках пересечения ребер и плоскости сечения находятся вершины многоугольника. Видимость сечения зависит от видимости ребер и граней, через которые проходит многоугольник сечения (рисунок 9).

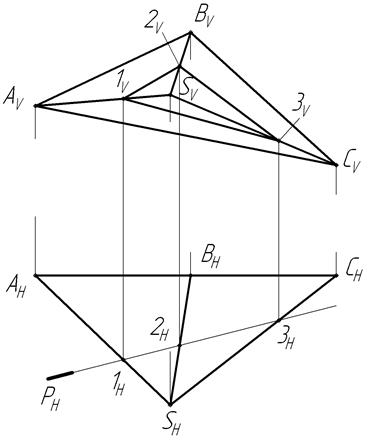
Рисунок 9 – Построение линии пересечения многогранника плоскостью

Задача Построить линию пересечения конуса фронтально-проецирующей плоскостью Q.

Алгоритм решения задачиЛиния пересечения конуса с заданной плоскостью–парабола (рисунок 10):

1 – вершина параболы,

2 и 3 – точки, ограничивающие параболу.

Ряд произвольных точек строят при помощи окружностей – параллелей h_v так, как это показано для точек 4 и 5.

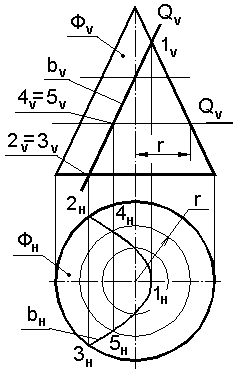
Рисунок 10 – Сечение конической поверхности вращения плоскостью Q

Задача Построить линию пересечения сферы фронтально-проецирующей плоскостью Р.

Алгоритм решения задачиВ сечении сферы получается окружность, которая проецируется на горизонтальную плоскость проекций в эллипс (рисунок 11).

Точки, принадлежащие линии сечения, соединяют плавной линией, с учетом её видимости.

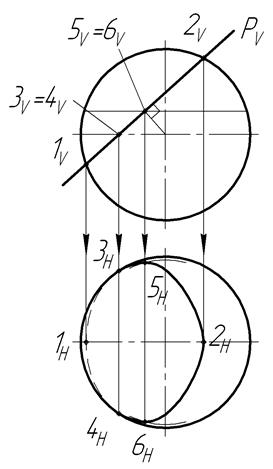
1 и 2 – высшая и низшая точки сечения, 3 и 4 – точки границы видимости, 5 и 6 – произвольные точки, которые строят при помощи окружностей – параллелей

Рисунок 11 – Сечение сферы плоскостью Р