Решение уравнений с использованием замены переменной

Метод пристального взгляда

Этот метод основан на следующем теоретическом положении: “Если функция 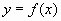возрастает в области определения и число 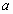входит в множество значений, то уравнение 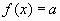имеет единственное решение.”

Для реализации метода, основанного на этом утверждении требуется:

а) Выделить функцию, которая фигурирует в уравнении.

b) Записать область определения данной функции.

c) Доказать ее монотонность в области определения.

d) Угадать корень уравнения.

t) Обосновать, что других корней нет.

f) Записать ответ.

Пример 1. .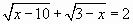

Наличие радикалов четной степени говорит о том, что подкоренные выражения должны быть неотрицательными. Поэтому сначала найдем область допустимых значение переменной .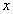

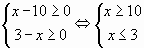
Очевидно, что левая часть уравнения не существует ни при одном значении неизвестного 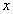. Таким образом, вопрос о решении уравнения снимается – ведь нельзя же осуществить операцию сложения в левой части уравнения, так как не существует сама сумма. Каков же вывод? Уравнение не может иметь решений, так как левая часть не существует ни при одном значении неизвестного .

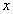Пример 2.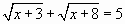

Рассмотрим функцию .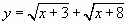

Найдем область определения данной функции:

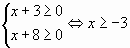
Данная функция является монотонно возрастающей.

Для 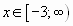эта функция будет принимать наименьшее значение при 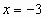, а далее только возрастать. 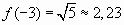. Число 5принадлежит области значения, следовательно, согласно утверждению .

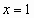Проверкой убеждаемся, что это действительный корень уравнения..

Метод возведения обеих частей уравнений в одну и ту же степень.

Теорема.

Если возвести обе части уравнения 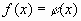(1) в натуральную степень 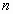, то уравнение 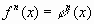(2) является следствием уравнения (1).

Доказательство. Если выполняется числовое равенство 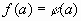, то по свойствам степени выполняется равенство 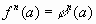, т.е. каждый корень уравнения (1) является и корнем уравнения (2), это значит, что уравнение (2) является следствием уравнения (1).

Если 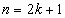, то справедливо и обратная теорема. В этом случае уравнения (1) и (2) равносильны.

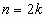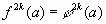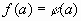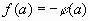Если , равенство справедливо, если выполняется хотя бы одно из равенств и . Значит уравнения (1) и (2) в этом случае не равносильны. Поэтому, если в ходе решения иррационального уравнения 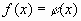приходилось возводить обе его части в степень с четным показателем, то могли появиться посторонние корни. Чтобы отделить их, проверки можно избежать, введя дополнительное требование 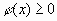. В этом случае уравнение 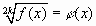равносильно системе 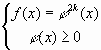. В системе отсутствует требование 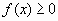, обеспечивающее существование корня степени 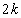, т.к. оно было бы излишним в связи с равенством .

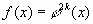Пример 1.

,

,

.

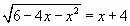
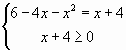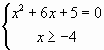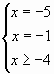Ответ: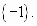

Если в уравнение входят несколько радикалов, то их можно последовательно исключать с помощью возведения в квадрат, получая в итоге уравнение вида 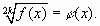При этом полезно учитывать область допустимых значений исходного уравнения.

Пример 2.

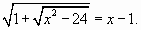
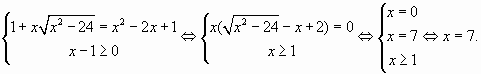
Ответ: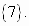

Решение уравнений с использованием замены переменной.

Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной.

Пример1.

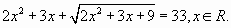
Пусть 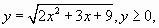тогда исходное уравнение примет вид:

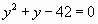, корни которого 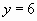и 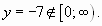Решая уравнение 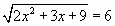, получаем 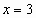и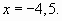

Ответ: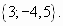

В следующих примерах используется более сложная замена переменной.

Пример 2

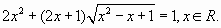
Перенесем в левую часть все члены уравнения и произведем дополнительные преобразования: .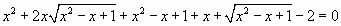

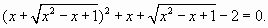
Замена 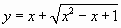приводит уравнение к виду 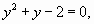корнями которого являются 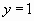и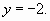

Осталось решить совокупность двух уравнений:

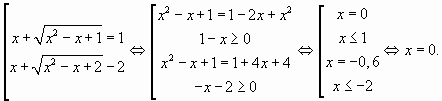
Ответ: