Распределение молекул по скоростям

Благодаря хаотичному движению, столкновениям между собой молекулы обладают разными скоростями. Об этом свидетельствует и барометрическая формула. Если бы все молекулы имели одинаковые скорости, распределение частиц по высоте было бы совершенно иным. В действительности, предположим, что все молекулы находятся у поверхности земли и имеют одинаковые скорости с вертикальной составляющей 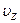. Эти молекулы поднялись бы на высоту 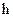, определяемую выражением

,

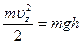т.е. до высоты

,

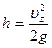после чего они вернулись бы к Земле с первоначальной кинетической энергией. При таких условиях атмосфера имела бы на высоте 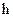резкую границу, за пределами которой ее не было бы. Опыт же показывает, что атмосфера резкой границы не имеет, ее плотность убывает с высотой в соответствии с барометрической формулой и простирается, поэтому практически бесконечно. Предположение о равенстве скоростей всех молекул противоречит, таким образом, опыту.

Следовательно, молекулы газа имеют различные скорости, так что среди них имеются как очень быстрые, так и очень медленные. Несмотря на полную хаотичность молекулярных движений, несмотря на случайный характер столкновений и вызываемых ими изменений скоростей молекул, их распределение по скоростям оказывается не случайным, не произвольным, и вполне определенным. Необходимо получить закон распределения молекул по скоростям. Прежде чем приступить к выводу закона распределения молекул по скоростям, необходимо выяснить, что значит распределение молекул по скоростям. С первого взгляда определить распределение молекул по скоростям означает, как будто бы, определить число молекул, обладающих той или иной заданной скоростью. Однако в такой постановке вопрос не имеет смысла, так как число молекул, имеющих точно заданную скорость, равна нулю, поскольку число различных скоростей бесконечно много, а число молекул конечно. Поэтому число молекул, приходящих на долю каждого произвольно заданного значения скорости, равно нулю. Вследствие этого вопрос о распределении молекул по скоростям должен быть сформулирован следующим образом: сколько молекул 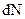из общего числа 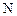имеют скорости 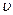в интервале от 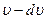до .

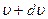Функция распределения

Очевидно, число частиц 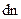в единице объема, скорости которых лежат в некотором интервале от 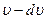до 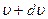тем больше, чем больше интервал 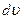, т.е.

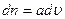, (3.39)

где 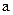- коэффициент пропорциональности. Надо отметить, что 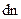зависит и от самой скорости. При одинаковых по величине интервалах 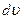, но при разных абсолютных значениях скорости число частиц 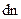будет различным. Это означает, что коэффициент пропорциональности 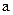в формуле (3.39) должен быть функцией скорости:

.

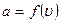Кроме того, 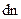должно быть также пропорционально числу частиц в единице объема и, таким образом, окончательно получаем:

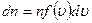. (3.40)

Эту формулу также записывают в виде

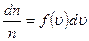, (3.41)

где 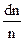- доля частиц, скорости которых лежат в интервале от 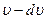до .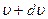

Функцию 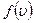называют функцией распределения. Если 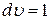, то .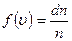

Таким образом, функция распределения численно равно доле частиц, скорости которых лежат в единичном интервале скоростей вблизи 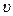. Существуют несколько методов определения функции распределения 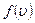. Функция распределения молекул по 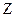компонентам скорости 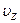можно получить из барометрической формулы (см. учебники Кикоин И.К., Кикоин А.К. "Молекулярная физика"). Она имеет вид:

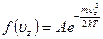, (3.42)

где 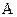- так называемая нормировочная постоянная. Знание функции 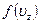позволяет определить, какая часть молекул в единице объема обладает скоростями от 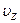до 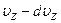, т.е.

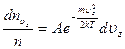. (3.43)

Эта величина не зависит от того, каковы составляющие скоростей молекул по осям Х и У. Поскольку в пространстве нет выделенных направлений, соотношение вида (3.43) справедливо для осей Х и У, т.е.

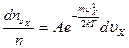, (3.44)

.

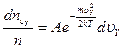Найдем значение 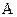, входящее в выражения (3.43) и (3.44). Для этого перепишем одно из них, например, (3.43) в виде:

.

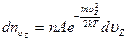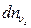- это число молекул в единице объема, составляющие скорости которых по оси 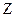лежат в пределах от 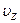до 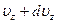. Если просуммировать это выражение по всем возможным значениям 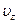от -¥ до +¥, то получим общее число молекул в единице объема, т.е. 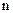, поскольку каждая молекула обладает какой-либо составляющей скорости по оси 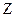. Таким образом,

,

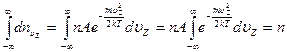откуда

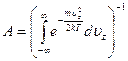. (3.45)

Для вычисления интеграла (3.45) введем новую переменную .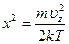

Тогда

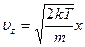и .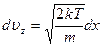

Отсюда

.

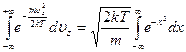Известно, что 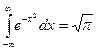. Тогда из (3.45) имеем:

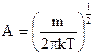. (3.46)

Следовательно, выражение для 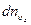примет теперь вид:

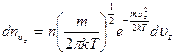. (3.47)

Определим число молекул в единице объема, обладающих скоростями, составляющие которых по трем осям координат лежат в пределах от 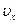до 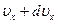(по оси Х), от 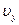до (по оси У) и от 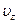до 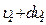(по оси Z). Будем рассуждать следующим образом. Отберем сначала из всех молекул в единице объема те молекулы, составляющие скоростей которых по оси Х лежат в пределах от 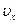до 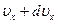. Число таких молекул согласно (3.44), равно

.

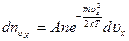По осям У и Z составляющие скоростей этих молекул могут быть любыми (от

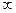- до + 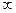). Какая часть из этого числа 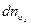имеет скорости, составляющие которых по оси У лежат в пределах от 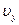до при любых 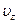. Согласно (3.44) для определения этого числа 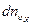надо умножить на 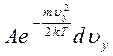. Значит, число молекул, у которых составляющие скорости по оси Х лежат в пределах от 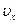до 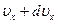и в то же время по оси У в пределах от 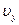до равно:

.

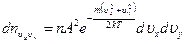Рассуждая таким же образом можно получить выражение для числа молекул 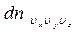, компоненты скорости которых одновременно лежат в пределах , ,

.

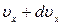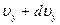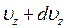
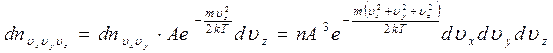Подставляя в полученную формулу выражение (3.46) для 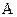, получим окончательно:

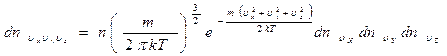. (3.48)

Дадим геометрическое истолкование этой формулы. Представим, что все молекулы, компоненты скоростей которых заключены в указанном выше интервале скоростей, собраны в начале координат и выпущены. Через одну секунду они все окажутся на расстоянии 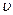от начального положения в кубике со сторонами 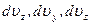,т.е. в объеме 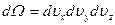. Концентрация молекул в этом кубике равна:

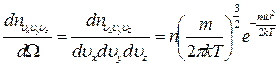, (3.49)

где .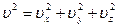

Формула Максвелла

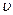Концентрация, определяемая формулой (3.49) не может зависеть от направления вектора скорости . Поэтому мы можем найти функцию распределения молекул по скоростям, независимо от их направления. Действительно, если собрать все молекулы единицы объема, скорости которых лежат в пределах от 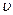до 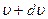, независимо от их направления и выпустить их, то они, разлетаясь по всем направлениям, через одну секунду окажутся равномерно распределенными в шаровом слое толщиной 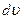и радиусом 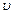. Это шаровой слой сложится из тех «кубиков», о которых говорилось выше. Плотность числа молекул или концентрация будет определяться опять формулой (3.49).Число молекул в шаровом слое будет равно произведению плотности молекул (формула (3.49) на объем шарового слоя 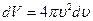, т.е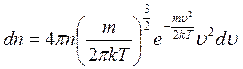

(3.50)

Если сравнить эту формулу с выражением (3.40), получим следующее выражение для функции распределения молекул по скоростям:

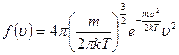. (3.51)

Эта функция называется функцией распределения Максвелла.

Вид этой функции приведен на рис. 3. Как видно из графика, функция обращается в нуль пр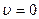и и 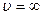, т.е. число неподвижных молекул, как и число молекул, движущихся с очень большой скоростью, равна нулю. Из кривой видно, что существует такая скорость 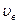, которой обладает максимальная доля молекул. Эта скорость называется наивероятнейшей скоростью.

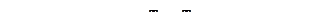Пользуясь кривой распределения Максвелла, можно графически определить число молекул, обладающих скоростями в заданном интервале 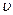и 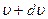. Это число выражается площадью с основанием 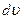и высотой 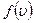. Распределение молекул по скоростям по формуле (3.51) зависит от температуры газа. Эта зависимость приведена на рис.4, из которого следует, что с повышением температуры скорости молекул возрастают, и вся кривая смещается в сторону больших скоростей. Площади, ограниченные этими кривыми и осью скоростей, пропорциональны общему числу частиц и не могут изменяться с температурой. Вследствие этого, максимумы кривых с повышением температуры понижаются. Надо отметить, что распределение Максвелла по скоростям является равновесным распределением. При отклонении система от состояния равновесия, максвелловское распределение нарушается. При возвращении в состояние равновесия благодаря столкновениям устанавливается опять максвелловское распределение.

Распределение Максвелла связано хаотичным движением молекул. Движение молекул полностью хаотично, если они распределены по скоростям в соответствии с формулой Максвелла. В противном случае, движением молекул является частично упорядоченным.