Перетин прямої з поверхнею
Загальні положення
1. Для визначення точки перетину прямої з багатогранником, доцільно використовувати проекціювальну площину.
Алгоритм розв’язання задачі на визначення точок перетину прямої лінії з поверхнею складається з трьох операцій (див рис. 18):
- через задану пряму слід провести допоміжну площину;
- побудувати лінію перетину допоміжної площини з поверхнею;
- визначити точки перетину отриманої лінії перетину з заданою прямою (точки входу та виходу).
Рис. 18
2.Для визначення точки перетину прямої з циліндричною поверхнею, допоміжну січну площину проводять паралельно твірним циліндра (див. рис. 19, а). Допоміжна площина перетинає бічну поверхню по прямих - твірних).

а б
Рис. 19
53.
3.Для визначення точки перетину прямої з конічною поверхнею, допоміжну площину проводять через вершину конічної поверхні (див. рис. 19, б). (тоді бічну поверхню допоміжна площина перетинає по твірних).
4.Для побудови точок перетину прямої з поверхнями обертання доцільно використовувати спосіб перетворення площин проекцій, так щоб пряма розміщувалась доцільним чином.
5. В деяких випадках, доцільно використовувати допоміжне косокутне проекціювання. Для циліндра використовують паралельне проекціювання (див рис. 19, а)., а для конусів – центральне, з центром проекціювання в вершині конуса (див. рис. 19, б).
Задачі для підготовки до практичних занять:
17.1. Побудувати проекції точок перетину прямих m і n з поверхнею піраміди.
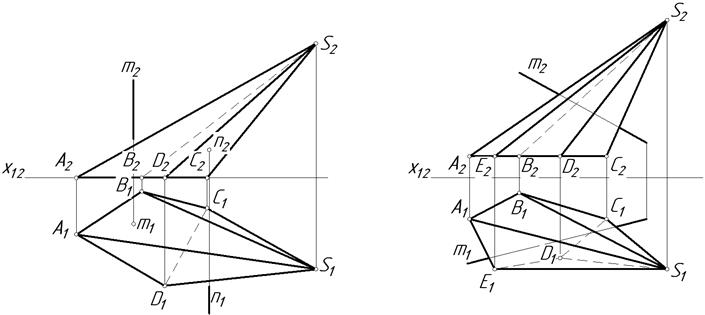
а б
54.
17.2. Побудувати проекції точок перетину прямої n з поверхнею: а) циліндра, б) конуса.
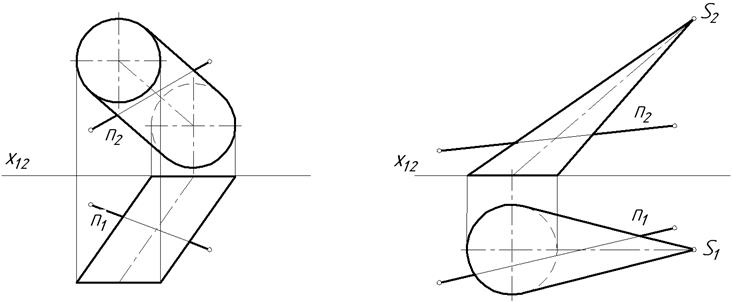
а б
Аудиторні задачі:
17.3. Побудувати проекції точок перетину прямої n з поверхнею призми.
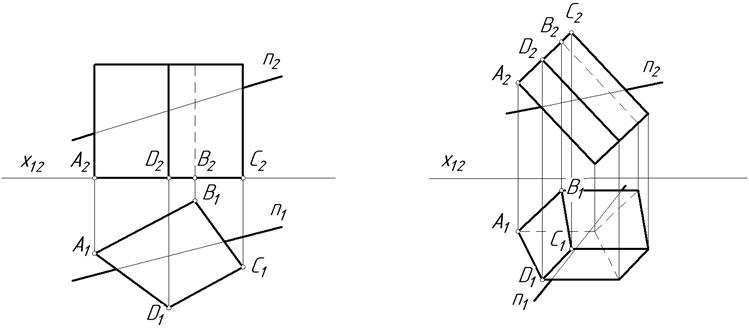
а б
55.
17.4. Побудувати проекції точок перетину прямої n з поверхнею: а) сфери,
б) обертання.
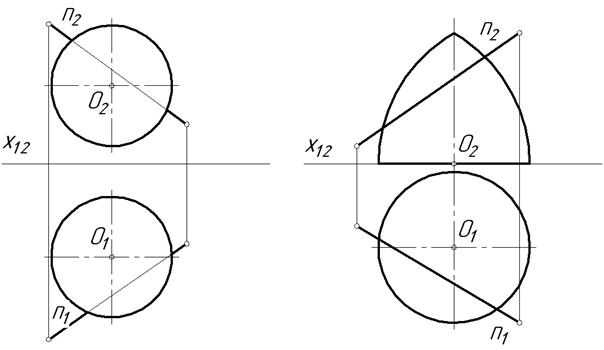
а б
56.
Розгортка поверхонь
Загальні положення
1. Розгорткою поверхні називається плоска фігура, яка утворена суміщенням поверхні з довільною площиною.
2. Між поверхнею і її розгорткою встановлюється взаємно-однозначна відповідність: кожній точці поверхні відповідає певна точка розгортки.
3. Поверхні бувають розгортні та не розгортні.
Поверхня розгортна, коли її можна сумістити без розривів та складок з площиною.
Поверхня не розгортна, коли її не можна сумістити без розривів та складок з площиною.
4. Властивості розгортних поверхонь:
а) довжина відповідних відрізків ліній на поверхні і на розгортці однакові;
б) кути між відповідними лініями, що перетинаються, на поверхні і на розгортці однакові;
в) площі відповідних фігур, окреслених замкнутими лініями, на поверхні і на розгортці однакові.
4. Дотична площина, проведена в будь-якій точці розгортної поверхні, дотикається до неї по прямій твірній.
5. Для побудови розгортки багатогранника необхідно визначити натуральні величини всіх граней і, послідовно прибудовуючи їх по суміжних ребрах, сумістити з площиною.
6. Загальний принцип побудови розгортки розгортної кривої поверхні: спочатку задана поверхня апроксимується (наближується) з достатньою точністю до багатогранної поверхні. Далі будується розгортка багатогранної поверхні, а одержані на розгортці точки, які належать кривій лінії на поверхні, сполучаються кривою лінією.
7. Для побудови розгорток призматичних і циліндричних поверхонь застосовують спосіб нормального перерізу або спосіб „розкочування”
8. Спосіб нормального перерізу ґрунтується на побудові розгортки нормального перерізу у вигляді прямої лінії, перпендикулярної до ребер або твірних поверхні.
9. Спосіб „розкочування” ґрунтується на суміщенні граней призми або ділянок циліндричної поверхні з площиною послідовним обертанням їх навколо ребер або твірних до суміщення з площиною.
10. Наближені (умовні) розгортки не розгортних поверхонь виконують шляхом їх апроксимації ділянками розгортних поверхонь і побудови розгортки цих ділянок.
57.
Задачі для підготовки до практичних занять:
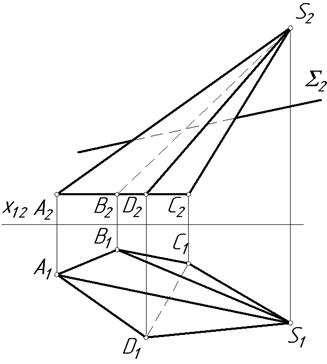
18.1. Побудувати розгортку поверхні похилої піраміди з нанесенням лінії перерізу площиною Σ.
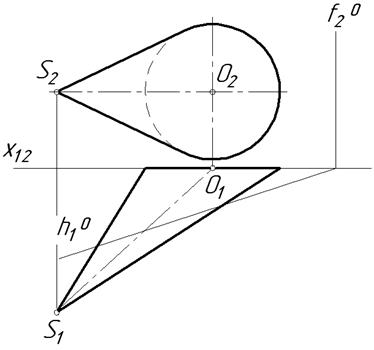
18.2. Побудувати повну розгортку зрізаного конуса.
58.
Аудиторні задачі:
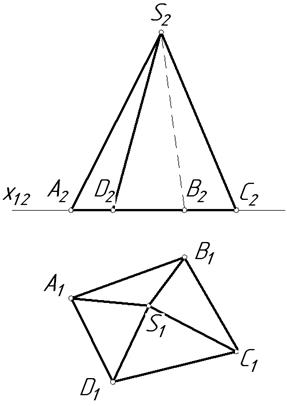
18.3. Побудувати розгортку заданої поверхні.
59.
Завдання 6. Перетин геометричних тіл прямою лінією
та побудова розгортки
Умова: Побудувати перетин заданих поверхонь призми, піраміди, циліндра, конуса, сфери відрізком прямої. Визначити видимість прямої на проекціях. Побудувати розгортку поверхні з нанесенням точок перетину прямої з поверхнею.
Завдання виконати на аркуші формату А4. Варіанти наведені в табл. 6 збірника завдань.
Приклад виконання завдання наведено в методичних вказівках.
60.
