Домашнее задание 16
16.8. Установить, что данное уравнение определяет эллипс, найти его центр C, полуоси и эксцентриситет: 4x2 + 3y2 – 8x + 12y – 32 = 0.
16.9. Установить, что данное уравнение определяет гиперболу, найти ее центр, полуоси, эксцентриситет и уравнения асимптот:
9x2 – 16y2 + 90x + 32y – 367 = 0.
16.10. Установить, что каждое из следующих уравнений определяет параболу, найти координаты ее вершины А и величину параметра p:
а)x2 = 2 – y; б)x = 2y2 – 12y + 14.
| 16.11. Записать квадратичную форму, порожденную матрицей: | а) 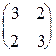 ; | б)  . |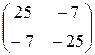
Привести уравнение кривой к каноническому виду:
16.12. 5x2 + 12xy – 22x – 12y – 19 = 0.
16.13. x2 – 4xy + 4y2 – 4x – 3y – 7 = 0.
16.14. 5x2 – 6xy + 5y2 – 32 = 0.
Дополнительное задание 16
Привести уравнение кривой к каноническому виду:
16.15. 16x2 + 25y2 + 32 x – 100y – 284 = 0.
16.16. 16x2 – 9y2 – 64x – 18y +199 = 0.
16.17. y = 4x2 – 8x + 7.
Ответы к занятию 16
16.1. C (3, – 1), a = 3, b = 
, e = 2/3.
16.2. C(2, – 3), a = 3, b = 4, e = 5/3, 4x – 3y – 17 = 0, 4x + 3y + 1 = 0.
16.3. a) (2, 0), p = 2; б) (6, – 1), p = 3.
16.5. Эллипс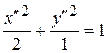 
. 16.6. Парабола y² 2 = 4 
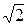x².
16.7.Гипербола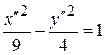 
.
16.8. C(1, – 2), a = 4, b = 2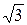 
, e = 1/2.
16.9. C(– 5, 1), a = 8, b = 6, e = 5/4, 3x + 4y + 11 = 0, 3x – 4y + 19 = 0.
16.10. а) (0, 2), p = – 1/2; б) (– 4, 3), p = 1/4.
16.12. Гипербола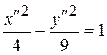 
, O² (1;1), e1= 
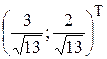, e2 = 
.
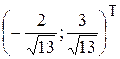16.13. Парабола y²¢2 =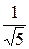 
x², O² (3; 2), e1 = 
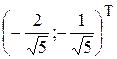, e2 = 
.
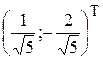16.14.Эллипс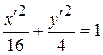 
, e1 = 
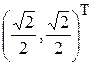, e2 = 
.
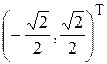16.15. Эллипс, a = 5, b = 4. 16.16. Гипербола, a = 4, b = 3.
16.17. Парабола, p = 1/8.
Занятие 17. Поверхности второго порядка
Изучаемый материал: алгебраические поверхности второго порядка: эллиптический, круговой, гиперболический и параболический цилиндры; эллипсоид и сфера; однополостный и двухполостный гиперболоиды; эллиптический и гиперболический параболоиды; классификация алгебраических поверхностей второго порядка; усвоение терминологии и признаков поверхностей по их каноническим уравнениям; построение графиков поверхностей по их каноническим уравнениям.
| 1. Определение вида поверхности | 17.1 - 17.8 | 17.11 - 17.14 | 17.17 - 17.21 |
| 2. Построение тел в пространстве | 17.9, 17.10 | 17.15, 17.16 |
Определить вид поверхности и сделать чертеж:
17.1. x2 + y2 - 9 = 0. 17.2. x2+ y2 - 2x - 4y - 4 = 0. 17.3. x2 - 2y + 1 = 0.
17.4. z = x2. 17.5. x2 = y2 + z2. 17.6. x2 = y2 - z2. 17.7. x = y2/4 + z2/9.
17.8. (x -1)2 + (y -3)2+ (z -1)2 = 4.
Построить тело, ограниченное поверхностями:
17.9. z = x2+ y2, z = 0, y = 1, y = 2x, y = 6 - x.
17.10. x = 0, y = 0, z = 0, 2x + 3y - 12 = 0, z = y2/2.