Примеры. 1. Исследовать на экстремумы функции:

1. Исследовать на экстремумы функции:

а) .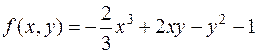

1) Ищем критические точки из условия одновременного обращения в нуль ее частных производных первого порядка в нуль:

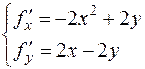
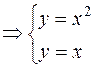
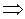система имеет 2 решения, а, значит, 2 критические точки: 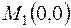и .

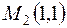2) Для исследования этих точек на экстремум найдем производные 2-го порядка и вычислим определитель:

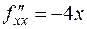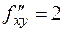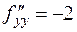, , , откуда .

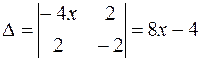В точке 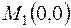: 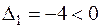, следовательно, согласно достаточному признаку, экстремума нет.

В точке 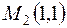: 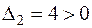, следовательно, согласно достаточному признаку, экстремум есть. Причем 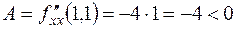, т.е. 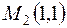- точка максимума.

3) .

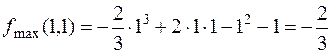б) .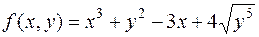

1) Ищем критические точки .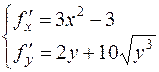

Из системы уравнений 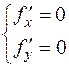находим 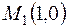и .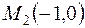

2) Найденные точки принадлежат области определения исследуемой функции:

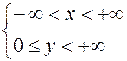(которая представляет собой половину плоскости хОу, лежащую выше оси Ох, включая и саму ось Ох).

Но эти точки расположены не внутри области определения, а на ее границе 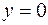, поэтому не являются критическими.

3) Частные производные первого порядка для данной функции существуют во всей области определения, поэтому и других критических точек функция не имеет. Следовательно, она не имеет экстремумов, согласно необходимому признаку.

Если не учесть, что граничные точки области определения функции не могут быть точками экстремума, то определив знак определителя точки 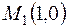, мы бы пришли к ошибочному заключению, что она есть точка минимума.

в) .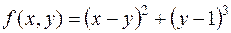

1) Ищем критические точки .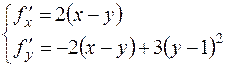

Решая систему уравнений ,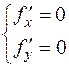

находим единственную точку 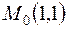, которая является единственной критической точкой функции.

2) Для исследования этой точки на экстремум воспользуемся необходимым признаком экстремума: найдем производные 2-го порядка и вычислим определитель:

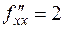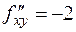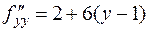, , , откуда .

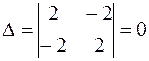Здесь определитель, как оказалось, не имеет знака, поэтому требуется дополнительное исследование. Чтобы установить, имеется ли экстремум в найденной критической точке 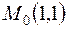, исследуем знак приращения функции вблизи нее:

.

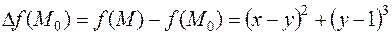Пусть точка 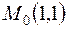лежит на биссектрисе .

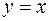Тогда .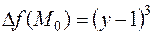

Если точка 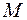будет расположена ниже 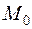, т.е. если ордината точки 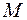: 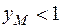, то 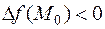. Если точка 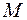будет выше 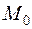, т.е. если ордината точки 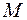: 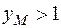, то и приращение функции .

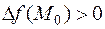Таким образом, вблизи 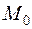разность 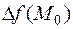не сохраняет знака и, следовательно, функция не имеет экстремума.

г) .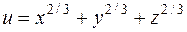

1) Ищем критические точки: , , .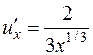

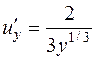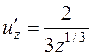Очевидно, что эти частные производные не обращаются в нуль ни при каких значениях 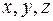. Они не существуют в точке 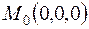, которая лежит внутри области определения функции (т.к. область определения данной функции – совокупность всех точек пространства). Поэтому данная точка – критическая точка.

2) Исследуя знак приращения функции вблизи найденной критической точки:

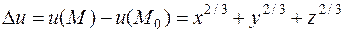
убеждаемся, что при любых, отличных от нуля значениях 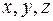, приращение сохраняет положительный знак. Следовательно, точка 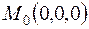- точка минимума и .

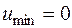Теорема 3. (Достаточные признаки экстремума для функции нескольких переменных).

Пусть 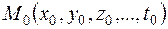- критическая точка функции 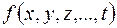, а сама функция дважды дифференцируема в критической точке. Обозначим:

, , , …

.

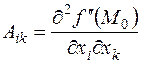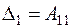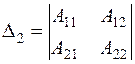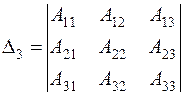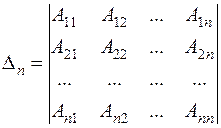Тогда

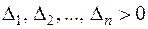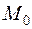1) если определители , то - точка минимума;

2) если знаки определителей 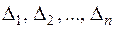, чередуются, начиная со знака минус, то 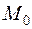- точка максимума.

Условный экстремум.

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение

j(х, у) = 0, которое называется уравнением связи.

Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.

Тогда u = f(x, y(x)).

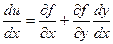
В точках экстремума:

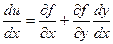=0 (1)

Кроме того:

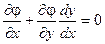(2)

Умножим равенство (2) на число l и сложим с равенством (1).

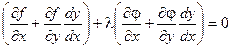
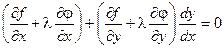
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:

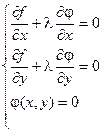
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.

Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:

2x + 3y – 5 = 0

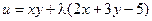
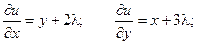
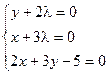
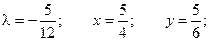
Таким образом, функция имеет экстремум в точке .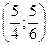

Использование функции Лагранжа для нахождения точек экстремума функции называется также методом множителей Лагранжа.

Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.