Примеры вычисления преобразования Фурье

Найдем преобразование Фурье для функции 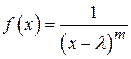, где m– натуральное число, а 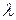– невещественная постоянная. Пусть, например, .

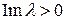Интеграл 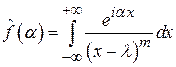абсолютно сходится при 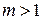, но при 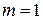он существует как условно сходящийся в смысле 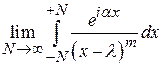. При любом 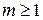этот интеграл удобно вычислять методом контурного интегрирования. При этом используется

Лемма Жордана. Пусть функция 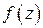голоморфна в полуплоскости 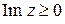всюду, за исключением изолированного множества особых точек, и 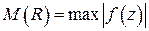на полуокружности 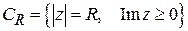стремится к нулю при 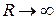(или по последовательности 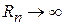такой, что 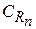не содержит особых точек 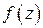). Тогда для любого 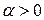интеграл

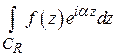
стремится к нулю при 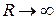(или по соответствующей последовательности ).

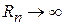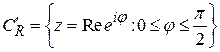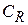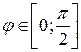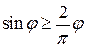Доказательство леммы Жордана. Обозначим через – правую половину . В силу выпуклости синусоиды при имеем и, значит, на 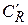справедлива

оценка 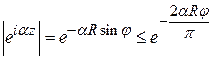. Поэтому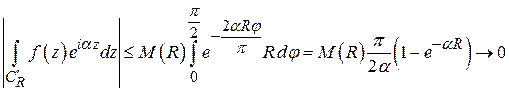

при .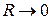

Оценка для 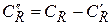проводится аналогично: .

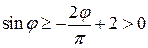Лемма Жордана доказана.

Для 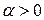рассмотрим контур 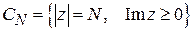так, чтобы выполнялась лемма Жордана для функци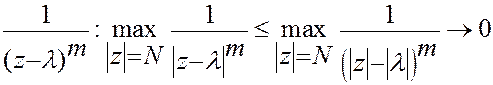и при . Внутри контура при достаточно большом значении N находится точка 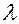– полюс подынтегральной функции. По теореме о вычетах

.

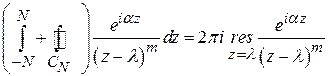Указанный вычет легко сосчитать, если разложить функцию 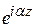в ряд Тейлора по степеням :

.

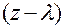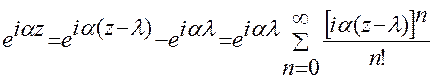Вычет есть коэффициент при 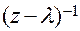; следовательно, для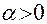

.

Устремляя , получаем для

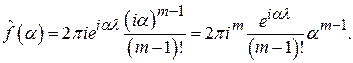
Для 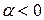надо рассмотреть полуокружность 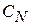в нижней полуплоскости. Здесь по теореме Коши об интеграле по замкнутому контуру от голоморфной функции, получим .

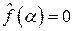Итак, при 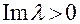имеем

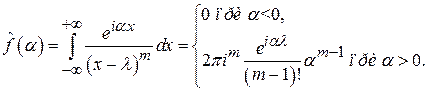
Для случая 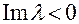аналогично можно найти

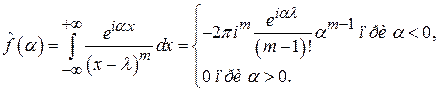
В обоих случаях функция 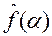экспоненциально убывает при .

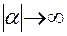Любая дробно-рациональная функция, не имеющая особенностей на вещественной оси и стремящаяся к нулю на бесконечности, разлагается на простейшие дроби вида , где 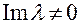. Поэтому полученные формулы позволяют написать преобразование Фурье от любой дробно-рациональной функции, при этом сохранится экспоненциальное убывание при .

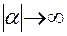Рассмотрим второй пример. Найдем преобразование Фурье от функции

, .

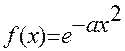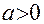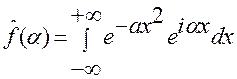– интеграл от аналитической функции 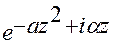по вещественной оси, z=x+iy. Так как

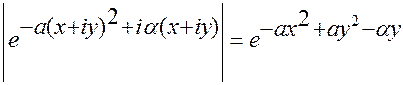, то в любой горизонтальной полосе 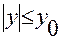подынтегральная функция при 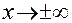стремится к нулю равномерно по y. Поэтому, используя теорему Коши, можно при интегрировании перейти на любую параллельную прямую в z –плоскости, не изменяя результата:

=

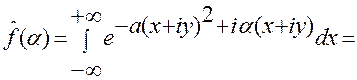
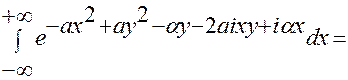
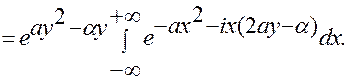
Положим 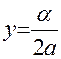, тогда 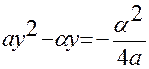и по известной формуле

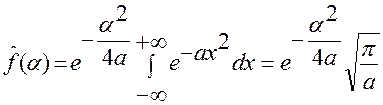. (Известная формула – интеграл вероятности ).

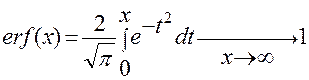В частности, для 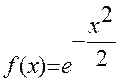, , 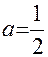получаем 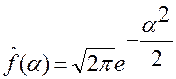– функцию того же вида, отличающуюся от исходной функции только множителем .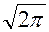