Приближенные вычисления с помощью дифференциала
Как уже известно, приращение 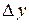 функции
функции 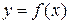 в точке x можно представить в виде
в точке x можно представить в виде 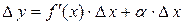 , где
, где 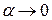 при
при 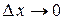 , или
, или 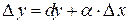 . Отбрасывая бесконечно малую
. Отбрасывая бесконечно малую 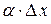 более высокого порядка, чем
более высокого порядка, чем 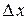 , получаем приближенное равенство
, получаем приближенное равенство
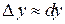 ,
,
причем это равенство тем точнее, чем меньше 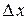 .
.
Это равенство позволяет с большой точностью вычислить приближенно прира-щение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому эта формула широко применяется в вычислительной практике.
Подставляя в равенство 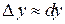 значения
значения 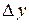 и
и 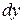 , получаем
, получаем
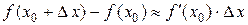
или
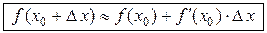 (16.12.)
(16.12.)
Формула (16.12.) используется для вычислений приближенных значений функции.
Пример 16.15. Вычислить приближенно 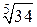 .
.
Решение. Рассмотрим функцию 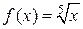 ;
;
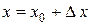 , где
, где 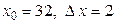 .
.
Находим первую производную функции и значение первой производной в точке 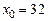 .
.
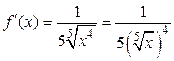 ;
;
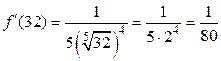 .
.
Находим значение функции в точке 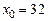 :
:
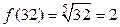 .
.
Тогда
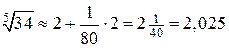 .
.
,
Дифференциалы высших порядков
Пусть 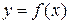 дифференцируемая функция, а ее аргумент x – независимая переменная. Ее первый дифференциал
дифференцируемая функция, а ее аргумент x – независимая переменная. Ее первый дифференциал 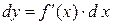 есть также функция x. Можно найти дифференциал этой функции.
есть также функция x. Можно найти дифференциал этой функции.
Дифференциалом второго порядка называется дифференциал от первого дифференциала, т.е.
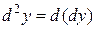 .
.
Найдем выражение второго дифференциала функции 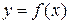 . Так как
. Так как 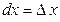 не зависит от x, то при дифференцировании считаем
не зависит от x, то при дифференцировании считаем 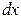 постоянным:
постоянным:
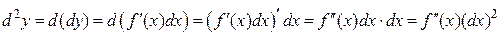 .
.
Таким образом, получаем
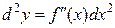 . (16.13.)
. (16.13.)
Равенство (16.13.) есть формула, по которой находится дифференциал второго порядка функции 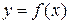 , если x – независимая переменная.
, если x – независимая переменная.
Аналогично определяется и находится дифференциал третьего порядка:
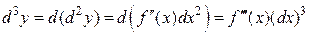 .
.
И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка: 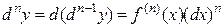 .
.
Отсюда находим, что 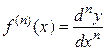 . В частности, при
. В частности, при 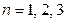 соответственно получаем:
соответственно получаем:
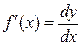 ,
, 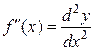 ,
, 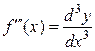 .
.
т.е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.
Отметим, что все приведенные выше формулы справедливы только, если x – независимая переменная. Если же функцию 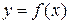 , где x есть функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
, где x есть функция от какой-то другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.
Используя формулу дифференциала произведения ( 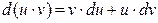 ), полу-чаем:
), полу-чаем:
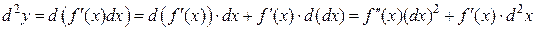 ,
,
т.е.
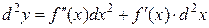 . (16.14.)
. (16.14.)
Сравнивая формулы (15.13.) и (15.14.), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое 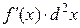 .
.
Ясно, что если x – независимая переменная, то
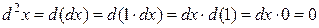
и формула (16.14.) переходит в формулу (16.13.)
Пример 16.16. Найти 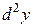 , если
, если 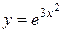 , x – независимая переменная.
, x – независимая переменная.
Решение. Находим последовательно 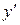 и
и 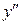 :
:
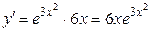 ;
;
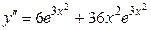 .
.
Тогда по формуле (16.13.) получаем
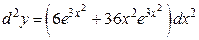 .
.
,
