Вопрос 10.1. Смешанное произведение векторов

Определение 10.1. Смешанным произведением трех векторов называется число

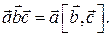
Геометрическое свойство смешанного произведения:

Теорема 10.1.Объём параллелепипеда, построенного на векторах 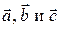равен модулю смешанного произведения этих векторов

,

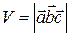или объём тетраэдра (пирамиды), построенного на векторах 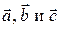равен одной шестой модуля смешанного произведения

.

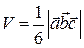Доказательство. Из элементарной геометрии известно, что объём параллелепипеда равен произведению высоты на площадь основания

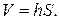
Площадь основания параллелепипеда S равна площади параллелограмма, построенного на векторах (см. рис. 1). Используя

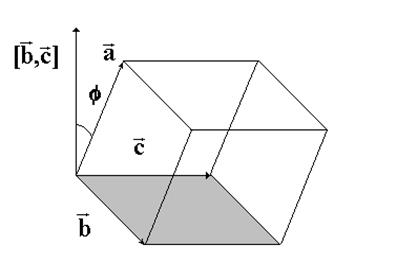
Рис. 1. К доказательству теоремы 1.

геометрический смысл векторного произведения векторов 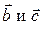, получаем, что

.

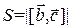Далее, если тройка векторов 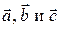является правой (как на рис. 1), то высота параллелепипеда равна проекции вектора 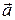на вектор 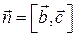, т.е.

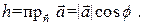
Отсюда получаем

.

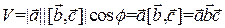Если тройка векторов 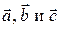левая, то вектор 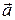и вектор 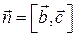направлены противоположно, тогда

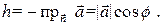
или

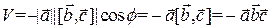
Таким образом, попутно доказано, что знак смешанного произведения определяет ориентацию тройки векторов 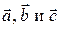( 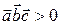‑ тройка правая и 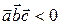‑ тройка левая).

Докажем теперь вторую часть теоремы. Из рис. 2 очевидно, что объем треугольной призмы, построенной на трех векторах 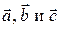равен половине объема параллелепипеда, построенного на этих векторах, то есть .

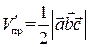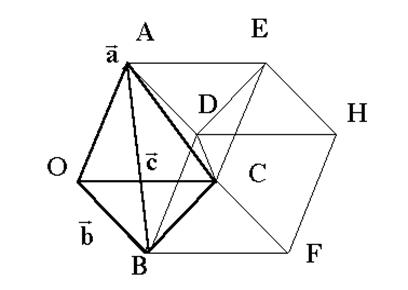
Рис. 2. К доказательству теоремы 1.

Но призма состоит из трех одинакового объема пирамид OABC, ABCD и ACDE. Действительно, объемы пирамид ABCD и ACDE равны, так как они имеют равные по площади основания BCD и CDE и одинаковую высоту, опущенную из вершины A. То же справедливо для высот и оснований пирамид OABC и ACDE. Отсюда

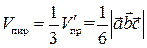
Конец доказательства.

Из теоремы 10.1 получаем условие компланарности трех векторов:

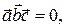
а так же условие принадлежности четырех точек пространства 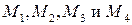одной плоскости

.

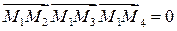Вопрос 10.2. Свойства смешанного произведения.

Свойство 10.1.Смешанное произведение линейно по каждому множителю

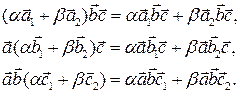
Доказательство.

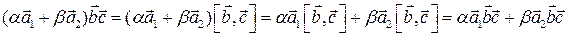
Аналогично доказываются две другие формулы.

Конец доказательства.

Свойство 10.2.Смешанное произведение векторов равно определителю третьего порядка, составленного из декартовых координат этих векторов

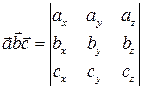, где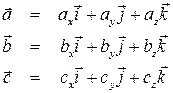

Доказательство. По определению смешанного произведения

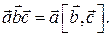
Так как

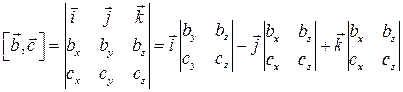
то, вычисляя скалярное произведение, получим

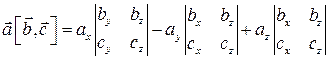
или

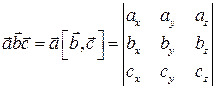
Конец доказательства.

Свойство 10.3.Перестановка двух соседних множителей в смешанном произведении меняет его знак на противоположный.

Доказательство. Перестановка двух соседних множителей эквивалентна перестановке соседних строк определителя, составленного из координат векторов. Как известно, такая перестановка меняет знак определителя на противоположный, а, следовательно, и знак самого смешанного произведения.

Конец доказательства.

Свойство 10.4.Циклическая перестановка векторов в смешанном произведении не меняет его величины.

Доказательство.Циклическая перестановка ‑ это перестановка, в которой первый объект становится третим, второй ‑ первым, третий вторым

1 2 3 Þ 2 3 1 .

Циклическую перестановку можно представить как композицию двух перестановок соседних объектов:

1 2 3 Þ 2 1 3 Þ 2 3 1

Тогда знак смешанного произведения согласно свойству 10.3 будет меняться дважды, и в конечном итоге останется без изменения.

Конец доказательства.