Смешанное произведение векторов
Определение.Смешанным произведением векторов  на
на  и на
и на  (будем обознрачать
(будем обознрачать 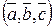 ) называется число, равное скалярному произведению вектора
) называется число, равное скалярному произведению вектора 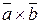 на вектор
на вектор  :
:
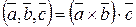 .
.
Геометрический смысл смешанного произведения описывает следующее утверждение.
Теорема.Пусть  ,
,  ,
,  - ненулевые некомпланарные векторы. Тогда смешанное произведение
- ненулевые некомпланарные векторы. Тогда смешанное произведение 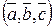 равно объему параллелепипеда, построеннного на этих векторах, отложенных из одной точки, взятому со знаком плюс, если тройка векторов
равно объему параллелепипеда, построеннного на этих векторах, отложенных из одной точки, взятому со знаком плюс, если тройка векторов  ,
,  ,
,  - правая, и со знаком минус, если эта тройка – левая.
- правая, и со знаком минус, если эта тройка – левая.
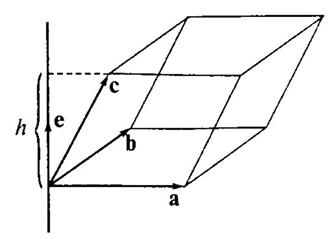 Доказательство. Восстановим параллелепипед, как указано в формулировке теоремы (см. рисунок). Площадь параллелограмма, построенного на векторах
Доказательство. Восстановим параллелепипед, как указано в формулировке теоремы (см. рисунок). Площадь параллелограмма, построенного на векторах  и
и  , равна числу
, равна числу 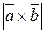 по определению векторного произведения. Тогда объем параллелепипеда определяется равенством:
по определению векторного произведения. Тогда объем параллелепипеда определяется равенством:
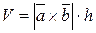 ,
,
где 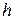 - высота параллелепипеда. Пусть
- высота параллелепипеда. Пусть 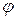 - угол между векторами
- угол между векторами 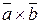 и
и  . Тогда
. Тогда
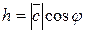 ,
,
если тройка векторов  ,
,  ,
,  - правая, и
- правая, и
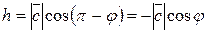 ,
,
Если указанная тройка векторов – левая. В результате имеем:
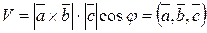 ,
,
если тройка векторов  ,
,  ,
,  - правая, и
- правая, и
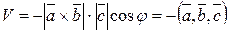 ,
,
если эта тройка векторов – левая. ■
Рассмотрим основные свойства смешанного произведения.
1. Смешанное произведение 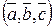 равно нулю тогда и только тогда, когда хотя бы один из векторов
равно нулю тогда и только тогда, когда хотя бы один из векторов  ,
,  ,
,  является нулевым или если рассматриваемые векторы компланарны.
является нулевым или если рассматриваемые векторы компланарны.
Доказательство.
Необходимость. Пусть 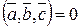 . Предположим, что
. Предположим, что  ,
,  ,
,  - ненулевые некомпланарные векторы. Тогда в соответствии с последней теоремой объем параллелепипеда, построенного на рассматриваемых векторах равен числу
- ненулевые некомпланарные векторы. Тогда в соответствии с последней теоремой объем параллелепипеда, построенного на рассматриваемых векторах равен числу 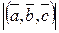 . Следовательно, это число больше нуля, и
. Следовательно, это число больше нуля, и 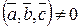 , что противоречит условию. Значит либо один из векторов является нулевым, либо векторы
, что противоречит условию. Значит либо один из векторов является нулевым, либо векторы  ,
,  ,
,  компланарны.
компланарны.
Достаточность.Если хотя бы один из векторов  ,
,  ,
,  - нулевой, то равенство нулю смешанного произведения
- нулевой, то равенство нулю смешанного произведения 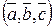 очевидно. Если векторы
очевидно. Если векторы  ,
,  ,
,  - компланарны, то вектор
- компланарны, то вектор 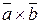 ортогонален вектору
ортогонален вектору  . Следовательно,
. Следовательно,
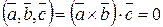 .■
.■
2. Если в смешанном произведении поменять любые два вектора местами, то изменится лишь знак этого произведения.
Доказательство. Если в смешанном произведении 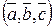 хотя бы один из векторов является нулевым или эти векторы компланарны, то утверждение данного свойства сразу следует из предыдущего свойства. Пусть
хотя бы один из векторов является нулевым или эти векторы компланарны, то утверждение данного свойства сразу следует из предыдущего свойства. Пусть  ,
,  ,
,  - ненулевые некомпланарные векторы. Воспользуемся теоремой итого пункта. При рассмотрении параллелепипеда, построенного на рассматриваемых векторах, замечаем, что любая замена местами векторов приводит лишь к смене ориентации тройки векторов
- ненулевые некомпланарные векторы. Воспользуемся теоремой итого пункта. При рассмотрении параллелепипеда, построенного на рассматриваемых векторах, замечаем, что любая замена местами векторов приводит лишь к смене ориентации тройки векторов  ,
,  ,
,  . Следовательно, если до такой замены смешанное произведение равнялось объему параллелепипеда, то после замены оно будет равняться этому объему с противоположным знаком, и наоборот. Таким образом, при этой замене меняется лишь знак смешанного произведения. ■
. Следовательно, если до такой замены смешанное произведение равнялось объему параллелепипеда, то после замены оно будет равняться этому объему с противоположным знаком, и наоборот. Таким образом, при этой замене меняется лишь знак смешанного произведения. ■
Для нахождения смешанного произведения обычно пользуются следующим утверждением.
Теорема.Пусть в ортонормированном базисе  ,
,  ,
, 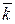 заданы три вектора:
заданы три вектора:
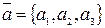 ,
,
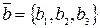 ,
,
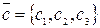 .
.
Тогда смешанное произведение 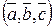 может быть найдено по формуле:
может быть найдено по формуле:
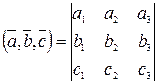 .
.
Доказательство. Воспользуемся определением смешанного произведения и формулой для нахождения векторного произведения. В результате будем иметь:
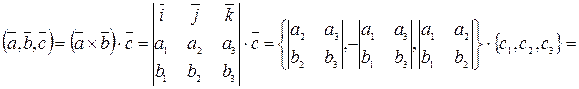
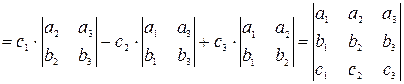 . ■
. ■
Пример.Даны вершины тетраэдра 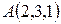 ,
, 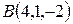 ,
, 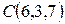 и
и 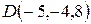 . Найти его объем и высоту, опущенную из вершины
. Найти его объем и высоту, опущенную из вершины 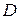 .
.
∆ Будем считать, что тетраэдр построен на векторах 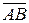 ,
, 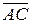 и
и 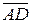 . Тогда его объем, равный шестой части объема параллелепипеда, определяется формулой:
. Тогда его объем, равный шестой части объема параллелепипеда, определяется формулой:
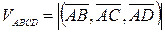 .
.
Найдем координаты введенных векторов:
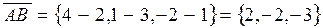 ,
,
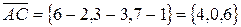 ,
,
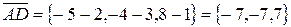 .
.
Тогда смешанное произведение векторов 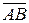 ,
, 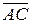 и
и 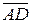 равно:
равно:
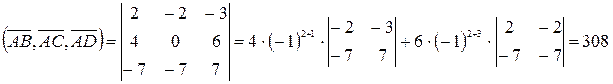 .
.
Соответственно,
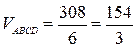 .
.
Для нахождения высоты тетраэдра воспользуемся известной формулой:
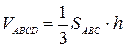 ,
,
где 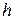 - высота тетраэдра, опущенная из вершины
- высота тетраэдра, опущенная из вершины 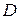 . Необходимо найти площадь треугольника
. Необходимо найти площадь треугольника 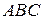 . Будем считать, что он построен на векторах
. Будем считать, что он построен на векторах 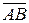 и
и 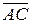 . Тогда
. Тогда
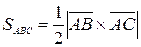 .
.
Воспользуемся формулой для нахождения векторного произведения. В результате будем иметь:
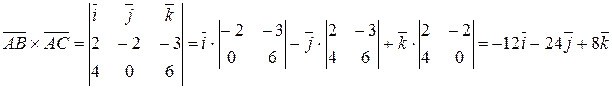 .
.
Следовательно,
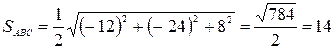 .
.
Тогда
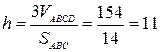 . ▲
. ▲
