Исследование функции на монотонность и экстремум

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Билет 1.Понятие функции и способы ее задания. Обратная функция. Сложная функция.

Понятие функции состоит из 3 частей: 1) Области определения D (совокупность значений x, для которых определяются значения функции у в силу правила f(x)); 2) Множества T, содержащего область значений E; 3) Правила, которое для каждого элемента из области D задаёт единственный элемент из области T.

Таким образом, функция есть зависимость, при которой каждому элементу x (- D соответствует единственный элемент y (- E. y=f(x),где х – независимая переменная, y – зависимая.

Способы задания функции:1) Аналитический (математическая формула, дающая воз-

можность вычислить значение функции); 2) Графический (Графиком функции y = f(x)

называется множество всех точек плоскости, координаты которых удовлетворяют

данному уравнению.); 3) При помощи таблицы; 4) При помощи словесного описания

Обратная функция:Пусть f: XàY и g: Y à X такие функции, что при х₁ ≠ x₂ è f(x₁) ≠ f(x₂). Тогда каждому y (- f(X) соответствует единственный элемент x (- X Такие образом g(x) является обратной функцией к f(x) и обозначается x=f^-1(y)

Сложная функция:Пусть даны функции f(x): X à Y и g(y): Y à Z. Причём D(g)=E(f). Тогда определена сложная функция φ: X à Z: φ=g(f(x))=gof(x) – композиция, т.е.применяй g, затем применяй f.

Билет 2.Предел функции в конечной точке и на бесконечности. Единственность предела в случае его существования.

В конечной точке: Пусть функция y=f(x) определена в некоторой окрестности точки x_0. Число А называется пределом f(x) в точке x₀ и пишут lim f(x)=A (xà x₀), если для любого ε>0 существует δ(ε)>0 такое, что для любых х, таких что 0<|x- x₀|<δ выполняется |f(x)-A| < ε

На бесконечности:Число А называют пределом f(x) при x à ∞, если для любого ε>0 существует число М(ε)>0 такое, что для любых х, таких что |x| > M, выполняется |f(x)-A| < ε. Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим.

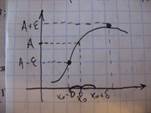Геометрический смысл:Взяв значение аргумента, принадлежащего интервалу

((х₀-δ); (x₀+δ)), значения функции обязательно попадают в интервал ((А-ε); (A+ε))

Примеры вычисления пределов по определению.

Единственность предела:f(x) определена в некоторой окрестности точки х₀ и lim f(x)=A,

lim f(x)=B (х à x₀). Тогда А=В, т.е.предел может быть только единственным.

Доказательство: Сначала напишем определение для А и В. Возьмём δ как наименьшее из

2ух чисел, т.е. рассмотрим δ=min(δ₁, δ₂) при |x-x₀|<δ.

|A-B| = |A-f(x)+f(x)-B| = |f(x)-A| + |f(x)-B| <= ε+ε = 2ε è A-B=0, A=B

Билет 3.Односторонние пределы.

Определение: Число А называется лево(право)-сторонним пределом функции y=f(x) в точке х₀, если функция определена на интервале (x₀-γ; x₀) ((x₀; x₀+ γ)) для γ>0 и для всех ε>0 найдётся δ= δ(ε)>0 такая, что 0<x₀-x< δ (0<x-x₀< δ) è |f(x)-A|< ε.

Обозначение: A=lim f(x) (xàx_0-0) (A=lim f(x) (xàx₀₊₀))

Для левостороннего предела рассматриваются значения аргумента слева от x_0: (x₀-δ; x₀)

Для правостороннего: x (- (x₀; x₀+δ)

Теорема:Для существования конечного предела функции в конечной точке необходимо и достаточно существования односторонних пределов функции в этой точке и их равенства друг другу. При этом сам предел равен каждому из односторонних.

Билет 4.Бесконечно малые величины (б.м.) и бесконечно большие (б.б.) величины. Свойства б.м. Связь б.б. и б.м. величин.

Функция α(х) называется бесконечно малой при х à x0 (б.м.), если lim α(х)=0 (xàx0).

Если lim α(х)/β(x) = 0 (xàx0), то α(х) называется б.м. более высокого порядка чем β(x), и пишут α(х)=oβ(x), xàx0.

Если lim α(х)/β(x) = C (xàx0, c<∞), то α(х) и β(x) называются б.м. одного порядка малости.

Если lim α(х)/β(x) = 1 (xàx0), то α(х) и β(x) называются называются эквивалентными и это обозначается

α(х) ~ β(x) при хàx0.

Если существует число k, такое что lim α(х)/(β(x))^k = C ≠ 0, то α(х) называется б.м. порядка k относительно β(x).

Y=F(x) называется бесконечно большой при xàx0, если lim F(x)= ∞ (xàx0)

Теорема о взаимосвязи:Пусть α =α(х) – б.м. в точке х0 (на ∞). Тогда β=1/ α(х) – б.б. в точке х0 (на ∞). И наоборот, если β= β(х) –б.б. в точке х0 (на ∞), то α(х)=1/ β(х) – б.м. в точке х0 (на ∞).

Доказательство:

Пусть α(х) определена в некторой точке х0 и б.м. в точке х0. Таким образом, для любого ε>0 найдётся δ =δ(ε) такая, что 0<|x-x0|< δ è | α(х)|< ε. Возьмём М=1/ε и найдётся δ =δ(ε)=δ(М) такая, что 0<|x-x0|< δ è |β(x)| =

|1/ α(х)| > 1/ ε = M è β(x) по опр. б.б.

1ый замечательный предел:это равенство lim sinx/x = 1 (xà0)

x~sinx~tgx~arcsinx~arctgx~(e^x-1)~ln(1+x)

1-cosx~x²/2

a^x-1~xlna

Свойства б.м.:

1)Сумма конечного числа б.м. величин также является б.м. величиной

2)Произведение бесконечно малых – б.м.

3)Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

Билет 5.Алгебраические свойства предела.

Пусть lim f(x)=A (xàx0), lim g(x) = B (xàx0), C-единственное число, тогда:

1) Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

.

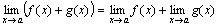Доказательство: Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть 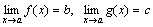.Тогда f(x)=b+α(x) и g(x)=c+β(x), где α и β – бесконечно малые функции. Следовательно, f(x) + g(x)=(b + c) + (α(x) + β(x)).

Так как b + c есть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

.

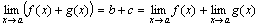2)Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

.

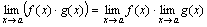Доказательство: Пусть 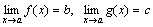. Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .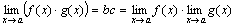

3)Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

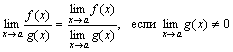Доказательство: Пусть 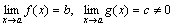. Следовательно, f(x)=b+α(x) и g(x)=c+β(x), где α, β – бесконечно малые. Рассмотрим частное

.

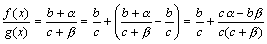Дробь 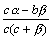является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c²≠0.

4)lim (C*f(x)) (xàx0) = C*A

5)lim C (xàx0) = C

Билет 6.Предельные переходы в неравенствах.

1)Пусть в некоторой проколотой окрестности точки х0 f(x) определена, удовлетворяет неравенству f(x)<=A и существует lim f(x)=f0 (xàx0). Тогда f0<=A.

Доказательство:

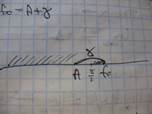Докажем от противного. Пусть существует lim f(x) (xàx0) = f0 = A+γ (γ-пол.число). Тогда для любого ε>0 найдётся δ>0 такая, что 0<|x-x0|< δ è |f(x)-f0|<ε.

Возьмём ε = γ/2>0. Тогда, с одной стороны |f(x)-f0|< γ/2 при 0<|x-x0|< D(γ).

С другой стороны |f(x)-f0|>= γ, т.к. f(x)<=A, a f0=A+ γ.

Полученное противоречие доказывает утверждение:

2) Лемма о 2ух милиционерах:

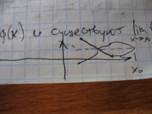Пусть для всех х (- Х выполняется неравенство f(x)<=φ(x)<=g(x) и существует lim f(x) = lim g(x) = A (x (- X). Тогда существует lim φ(x) = A.

3) Обобщение леммы:

Пусть для любого х (- Х f(x)<=φ(x)<=g(x) и существует lim f(x) = А, lim g(x) = B.

При этом, A<=B. Тогда, если существует lim φ(x) = С, то A<=C<=B

4) Теорема о существовании предела монотонной ограниченной функции:

Пусть f(x) монотонно возрастает (убывает) на [A; +∞). A – некоторое действительное число, f(x)<=M (f(x)>=m) для всех x (-[A; +∞). Тогда существует lim f(x) (xà+∞) <= M (lim f(x) (xà+∞) >= m). Аналогичные результаты верны для промежутка (-∞; B], где B-некоторое действительное число

5) Теорема о пределе сложной функции:

Пусть y=f(U(x)) – сложная функция. lim U(x) = U₀. lim f(U) (UàU₀) = f₀. Тогда lim f(U(x)) = f₀.

Билет 7.Теорема о существовании предела ограниченной монотонной функции.

Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Теорема: Пусть f(x) монотонно возрастает (убывает) на [A; +∞). A – некоторое действительное число, f(x)<=M (f(x)>=m) для всех x (-[A; +∞). Тогда существует lim f(x) (xà+∞) <= M (lim f(x) (xà+∞) >= m). Аналогичные результаты верны для промежутка (-∞; B], где B-некоторое действительное число.

Билет 8.Теорема о пределе сложной функции.

Сложная функция:Пусть даны функции f(x): X à Y и g(y): Y à Z. Причём D(g)=E(f). Тогда определена сложная функция φ: X à Z: φ=g(f(x))=gof(x) – композиция, т.е.применяй g, затем применяй f.

Теорема:Пусть y=f(U(x)) – сложная функция. lim U(x) = U₀. lim f(U) (UàU₀) = f₀. Тогда lim f(U(x)) = f₀.

Билет 9.Первый замечательный предел.

1ый замечательный предел:это равенство lim sinx/x = 1 (xà0)

x~sinx~tgx~arcsinx~arctgx~(e^x-1)~ln(1+x)

1-cosx~x²/2

a^x-1~xlna

Доказательство:

Рассмотрим односторонние пределы 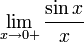и 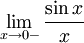и докажем, что они равны 1.

Пусть 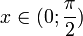. Отложим этот угол на единичной окружности (R = 1).

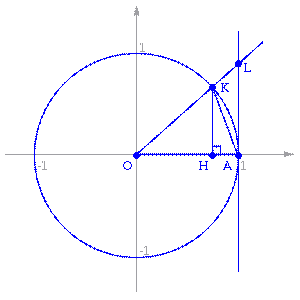Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

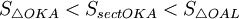(1)

(где S_sectOKA — площадь сектора OKA)

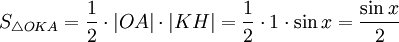
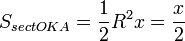
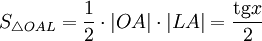
(из : | LA | = tgx)

Подставляя в (1), получим:

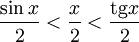
Так как при :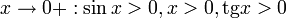

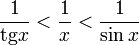
Умножаем на sinx:

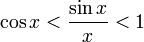
Перейдём к пределу:

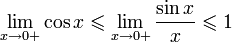
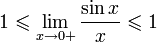
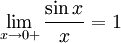
Найдём левый односторонний предел:

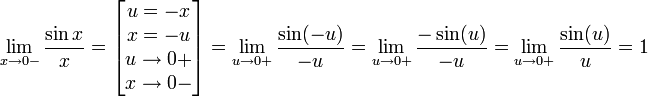
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Билет 10.Предел последовательности. Второй замечательный предел для последовательностей и функций.

Последовательность: Если каждому числу n натурального ряда чисел 1, 2, ..., n, ... ставится в соответствие поопределенному закону некоторое вещественное число x_n, то множество вещественных чисел x₁, x₂, x₃, ..., x_n мы назовем числовой последовательностью или просто последовательностью. Сокращенно последовательность обозначается - {x_n}.

Число А называется пределом последовательности {x_n}, если для любой ε-окрестности точки А найдётся натуральное число N, что все значения x_n, для которых n>N, попадут в ε-окрестность точки А.

2ой замечательный предел.Как известно, предел числовой последовательности

x_n=(1+1/n)ⁿ, n (- N, имеет предел равный e: lim (1+1/n)ⁿ = e (nà ∞).

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что 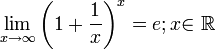. Рассмотрим два случая:

1. Пусть 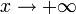. Каждое значение x заключено между двумя положительными целыми числами: 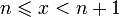, где 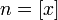— это целая часть x.

Отсюда следует: 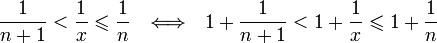, поэтому

.

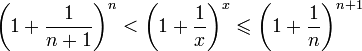Если 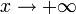, то 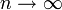. Поэтому, согласно пределу 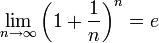, имеем:

.

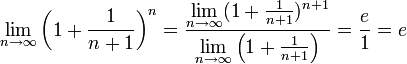
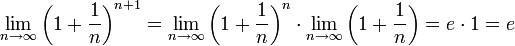По признаку (о пределе промежуточной функции) существования пределов .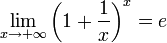

2. Пусть 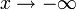. Сделаем подстановку − x = t, тогда

.

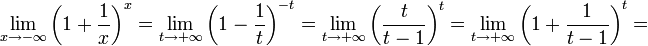
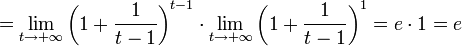Из двух этих случаев вытекает, что 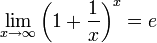для вещественного x.

Билет 11.Сравнение б.м. Эквивалентные б.м. Таблица основных эквивалентностей. Порядок малости.

Функция α(х) называется бесконечно малой при х à x0 (б.м.), если lim α(х)=0 (xàx0).

Если lim α(х)/β(x) = 0 (xàx0), то α(х) называется б.м. более высокого порядка чем β(x), и пишут α(х)=oβ(x), xàx0.

Если lim α(х)/β(x) = C (xàx0, c<∞), то α(х) и β(x) называются б.м. одного порядка малости.

Если lim α(х)/β(x) = 1 (xàx0), то α(х) и β(x) называются называются эквивалентными и это обозначается

α(х) ~ β(x) при хàx0.

Если существует число k, такое что lim α(х)/(β(x))^k = C ≠ 0, то α(х) называется б.м. порядка k относительно β(x).

Y=F(x) называется бесконечно большой при xàx0, если lim F(x)= ∞ (xàx0)

Таблица основных эквивалентностей:

Если lim sinx/x = 1 (xà0), тогда:

x~sinx~tgx~arcsinx~arctgx~(e^x-1)~ln(1+x)

1-cosx~x²/2

a^x-1~xlna

Билет 12.Непрерывность функции в точке и на промежутке. Непрерывность суммы, разности, произведения и частного (при условии, что знаменатель не обращается в 0) непрерывных функций. Непрерывность сложной функции. Непрерывность элементарных функций.

Определение. Функция y=f(x) называется непрерывной в точке x0, если: 1) f(x) определена в некоторой окрестности точки х0; 2) Существует lim f(x) (xàx0); 3) lim f(x) = f(x0). Функция называется непрерывной на промежутке, если она непрерывна во всех точках этого промежутка.

Геометрический смысл.Функция называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. Геометрически график непрерывной функции представляет собой непрерывную линию. Легко видеть, что функция непрерывна в точке х0 тогда и только тогда, когда односторонние пределы функции в этой точке существуют и равны между собой, а также значению функции в этой точке.

Теорема о действиях с непрерывной функцией:

Пусть f(x) и g(x) непрерывны в точке х0.

1) f(x)+-g(x)

2) f(x)*g(x)

3) f(x)/g(x), если g(x0) ≠ 0

Доказательство:

lim (f(x)+-g(x)) (xàx0) = lim f(x) +- lim g(x) = f(x0) +- g(x0)

Непрерывность сложной функции.Пусть f(x) – непрерывная в т. х0, а g(t) в т. t0=f(x0). Тогда функция g(f(x)) непрерывна в точке х0. Доказательство вытекает из теоремы о пределе сложной функции.

Непрерывность элементарных функций.Все основные элементарные функции непрерывны на своей области определения.

Билет 13.Точки разрыва и их классификация. Исследование функции на непрерывность.

Определение. Точки, в которых предел функции не существует или существует, но не равен значению функции в этой точке называются точками разрыва.

Устранимый разрыв (1ый род).Пусть существуют lim f(x) (xàx0-) и lim f(x) (xà x0+); они равны друг другу, но не равны значению функции в данной точке. Тогда x0 – устранимая точка разрыва

Разрыв типа скачок (1ый род).Пусть существуют конечные односторонние пределы функции f(x) в точке х0, не равные друг другу. Тогда х0 – точка разрыва 1го рода типа скачок

Разрыв второго рода.Пусть в точке х0 хотя бы один из односторонних пределов функции не существует или равен бесконечности. Тогда х0 – точка разрыва 2го рода.

Билет 14.Свойства функций, непрерывных на отрезке.

Теорема 1.Пусть функция y=f(x) непрерывна на отрезке [a; b]. Тогда найдутся х1, х2 (- [a;b] такие, что для всех х (- [a;b] выполняется неравенство: m = f(x1) <= f(x) <= f(x2) = M. То есть непрерывная на отрезке функция достигает на этом отрезке своего наименьшего значения m и наибольшего M.

Следствие: непрерывная на отрезке функция ограничена на нём.

Теорема 2.Пусть f(x) (- C[a;b] и f(a)*f(b)<0 (т.е. на концах отрезка функция имеет разные знаки). Тогда найдётся такое x0 (- (a;b), что f(x0) = 0.

Теорема 3.Пусть f(x) (- C[a;b] и f(a) ≠ f(b). Тогда для любого y* (- [f(a); f(b)], если f(а) < f(b) или y* (- [f(b); f(a)], если f(b) < f(a) найдётся x* (- [a;b]: f(x*)=y*, т.е. если на концах отрезка функция принимает не равнее друг другу значения, тогда она принимает и все промежуточные между этими значения.

Теорема 4.Пусть f(x) (- C[a;b] и m-наименьшее, а M-наибольшее значения функции f(x) на [a;b]. Тогда для любого у* (- [m; M] найдётся х* (- [a; b] такое, что f(x*)=y*, т.е. непрерывная на отрезке функция не только принимает наибольшее и наименьшее значения, но и пробегает все промежуточные.

Для монотонной непрерывной функции всегда найдётся обратная!

Рисунки

Билет 15.Задача о нахождении мгновенной скорости. Производная функции в точке. Геометрический смысл. Уравнения касательной и нормали к графику функции.

Задача. Пусть материальная точка M движется неравномерно по некоторой прямой. Каждому значению времени t соответствует определённое расстояние OS=M до некоторой фиксированной точки О. Это расстояние зависит от истёкшего времени t, т.е. t=S(t). Это равенство называют законом движения точки. Требуется найти скорость движения точки.

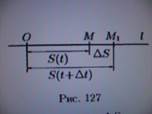Если в некоторый момент времени t точка занимает положение М, то в момент времени t+∆t (∆t – приращение времени) точка займёт положение М1, где ОМ1=S+∆S. Таким образом, перемещение точки М за время ∆t будет ∆S=S(t+∆t)-S(t). Отношение ∆S/∆t выражает среднюю скорость движения точки за время ∆t (Vср=∆S/∆t). Чем меньше ∆t тем точнее средняя скорость выражает мгновенную. Предел средней скорости движения при стремлении к нулю промежутка времени ∆t называется мгновенной скоростью: V=lim ∆S/∆t (∆tà0)

Определение.Предел отношения приращения функции y=f(x) к приращению аргумента

при x=x0 называется производной функции y=f(x) в точке х0, если он существует и

конечен. f ‘x при х=х0 = lim ∆f(x)/ ∆x (∆xà0) = lim (f(x)-f(x0))/(x-x0) (xàx0)

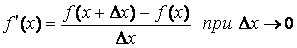
Обозначение.y’, y’(x), f ‘(x), dy/dx итд.

Геометрический смысл.Если к графику функции y=f(x) в точке с абциссой x=a можно

провести касательную, непараллельную оси y, то f’(a) выражает угловой коэффициент

касательной. k=f ‘(a), f ‘(a)=tgα

Касательная. Прямая называется касательной к графику функции y=f(x) в т. х0=(x0; f(x0)), если: 1) Прямая пересекается с графиком функции в точке х0; 2) В некоторой окрестности этой точки нет других пересечений; 3) Для всех х из этой окрестности график лежит по одну сторону от касательной. y=y0+f ‘(x0)(x-x0)

Нормаль.Нормалью к графику функции y=f(x) в точке х0 называется прямая перпендикулярная касательной к графику функции в этой точке. k_норм = -1/k_кас = -1/f ‘(x0) è y = -1/f ‘(x0)*(x-x0)+y0

Билет 16.Дифференцируемость функции в точке. Необходимое и достаточное условие дифференцируемости. Связь непрерывности и дифференцируемости функции. Логарифмическая производная.

Определение. Функция y=f(x) называется дифференцируемой в точке х0, если она имеет (конечную) производную в этой точке.

Необходимое и достаточное условие дифференцируемости.Для того, чтобы функция y=f(x) была дифференцируема в точке х0 необходимо и достаточно, чтобы в некоторой окрестности точки х0 её приращение имело вид: ∆y=A*∆x+α(x)*∆x, где А-конечное число, α(х)-б.м. в т. х0

Доказательство:

α(х)-б.м. в т. х0 è lim α(х)=0

1) Необходимость.

Пусть y=f(x) – диф. в т. х0, т.е. существует конечный lim ∆y/∆x = f ‘(x0). Обозначим f ‘(x0) = А < ∞. Рассмотрим функцию α(х) = -А+∆y/∆x. Тогда lim ∆y/∆x = lim (-A+ α(х)) = -A + lim ∆y/∆x = -A+A = 0. Следовательно α(х) – б.м. в точке х0.

2) Достаточность

Пусть в некоторой окрестности точки х0 ∆y = A*∆x + α(х)*∆x. lim ∆y/∆x = lim (A+ α(х)) = A+0 = А (существует и конечен). Т.е. функция диф. в т. х0.

Утверждение данной теоремы означает, что главной частью приращения диф. ф. является линейная часть. Нелинейная часть имеет более высокий порядок малости.

Связь непрерывности и дифференцируемости функции.Если y=f(x) – дифференцируема в точке х, то она непрерывна в этой точке.

Доказательство:

f(x) – диф. в т. х0 è по теореме 1 ^ её приращение ∆y=A*∆x+α(x)*∆x. Тогда при ∆xà0 получаем ∆yà0. Т.е. f(x)àf(x0) при xàx0, а это означает что функция непрерывна lim f(x) = lim f(x0)

Логарифмическая производная. Часто применяется для упрощения нахождения производной некоторых функции, например сложнопоказательных.

(log_ax)’=1/(x*lna)

(lnx)’=1/x

Билет 17.Правила дифференцирования. Производная суммы, произведения, частного дифференцируемых функций. Производная обратной функции. Производная сложной функции.

1) (U(x)+-V(x)) = U’(x)+-V’(x)

Доказательство:

Пусть ∆xà0. ∆(U+V)= ∆U+∆Vèlim ∆(U+V)/ ∆x (∆xà0) = lim (∆U+∆V)/∆x = lim ∆U/∆x + lim ∆V/∆x = U’ + V’

2) (U(x)*V(x))’=U’(x)*V(x)+U(x)*V’(x)

Доказательство:

Пусть ∆xà0. ∆(U*V) = (U+∆U)(V+∆V)-UV = UV+U∆V+V∆U+∆U∆V-UV;

(UV)’ = lim ∆(UV)/ ∆x = lim (U∆V+V∆U+∆U∆V)/∆x = сумма лимитов = V*lim ∆U/∆x + U*lim ∆U/∆x + lim ∆U/∆x * lim ∆V (∆xàбеск.) = VU’+UV’+U’*0.

3) (U(x)/V(x))’ = (U’(x)*V(x) – U(x)*V’(x))/V²(x)

Производная обратной функции.Пусть функция y=f(x) определена и дифференцируема в некоторой окрестности точки х0, f ‘(x0) ≠ 0. Пусть также в некоторой окрестности точки y0=f(x0) определена и дифференцируема обратная функция x=g(y) (x=f^-1(y)). Тогда производная обратной функции в точке у0 находится по формуле: x’(y0) = 1/f ’(x0) или g(y0)=1/f(x0), g-обр. f.

Доказательство:

g’(x) = lim ∆x/∆y (∆yà0) = lim 1/(∆y/∆x) = 1/lim ∆y/∆x (∆xà0) = 1/f(x0)

Производная сложной функции.Пусть функция x=φ(t) диф. в т. t0 и функция y=f(x) диф. в точке x0=φ(t0). Тогда сложная функция y(φ(t)) диф. в точке t0: y_t’(t0) = f_x’(x0)* φ_t(t0)

Доказательство:

y’(t0) = lim (∆y(φ(t)))/∆t (tàt0) = lim (∆y*∆x)/( ∆x*∆t) = lim ∆y/∆x * lim ∆x/∆t = y_x’(x0) * x_t(t0)

Билет 18.Таблица производных. Вывод производных логарифмической, показательной, степенной и основных тригонометрических функций (sin x, tg x).

(C)’ = 0

(x)’ = 1

(kx+b)’ = k

(x²)’ = 2x

(xⁿ)’ = n*x^n-1

(кор. x)’ = 1/(2кор.x)

(1/x)’ = - 1/x²

(sinx)’ = cosx

sinα-sinβ = 2sin((α-β)/2)*cos((α+β)/2)

y’=lim (sin(x+∆x)-sinx)/∆x (∆xà0) = lim (2sin(∆x/2)*cos((x+∆x)/2))/2*∆x/2 = cosx

(cosx)’ = -sinx

(tgx)’ = 1/cos²x

по правиду дифференцирования (деление)

(ctgx)’ = - 1/sin²x

(log_ax)’ = 1/(x*lna)

y’ = lim (log_a(x+∆x)-log_ax)/∆x (∆xà0) = lim (log_ax+∆x/x)/∆x = lim loga (1+ ∆x/x)/x*∆x/x = 1/x lim loga (1+∆x/x)^x/∆x = 1/x ln_ae = результат

(lnx)’ = 1/x

(e^x)’ = e^x

(a^x)’ = a^x*lna

y=a^x и x=log_ay – взаимообр. y_x’ = 1/x_y’, т.е. (a^x)’ = 1/(1/y*lna) = a^x*lna

(кор. х n-ой ст.)’ = 1/(n*кор х n-ой ст. из x^n-1)

(|x|)' = x/|x|

(arcsinx)’ = 1/кор. из 1-x²

(arccosx)’ = -1/кор. из 1-x²

(arctg)’ = 1/(1+x²)

(arcctg)’ = -1/(1+x²)

(1/x^c)’ = - c/x^c+1

Билет 19.Производные функций, заданных неявно и параметрически. Производные высших порядков.

Неявно. Под неявным заданием функции понимают задание функции в виде уравнения F(x; y)=0 (1) неразрешённого относительно у. Производная неявно заданной функции находится путём дифференцирования по х обеих частей выражения 1. Затем y’ выражаем через у и х.

Параметрически.Пусть зависимость между аргументом и функцией задана параметрически в виде 2 уравнений в системе: 1) x=x(t); 2) y=y(t), где t – вспомогательная переменная, называемая параметром. Найдём производную y_x’: t_x’=1/x_t’ (обратная функция). Функцию y=f(x) можно рассматривать как сложную функцию y=y(t), где t=φ(x). По правилу дифференцирования сложной функции имеем: y_x’=y_t’*t_x’. В итоге получаем: y_x’=y_t’*1/x_t’, т.е. y_x’=y_t’/x_t’

Производные высших порядков.Производной 2го порядка называется производная от первой производной, если обе производные существуют. Производной n-ого порядка от функции y=f(x) называется производная от n-1 производной, если существуют все производные от 1го до n-го порядка включительно. y’’, yⁿ

Билет 20.Дифференциал. Его геометрический смысл. Инвариантность формы первого дифференциала. Применение дифференциала в приближенных вычислениях.

Определение.Дифференциалом функции y=f(x) в точке х0 называется главная линейная часть приращения функции в точке х0 и обозначается dy = f ‘(x0)dx = f ‘(x0)∆x

Инвариантность формы первого дифференциала.Пишем определение. Пусть x=U(t); dx=U’(t)dt. Рассмотрим сложную функцию y=f(U(t)) и возьмём производную dy/dt f_u’U * U_t’ è dy = f ’(U)*U ’(t)dt =

= f ‘(U)*dU

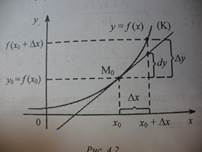Геометрический смысл.Дифференциал функции y=f(x) в точке х0 есть приращение ординаты касательной, проведённой к графику функции в точке M0(x0; y0), при приращении аргумента, равном ∆x. При ∆xà0 имеем ∆y≈dy, откуда получаем формулу приближённого вычисления значения функции в точке:

f(x0+∆x) ≈ f(x0)+f ‘(x0) ∆xили f(x) ≈ f(0)+f ‘(0)x

Примеры.

Билет 21.Дифференцирование функций, заданных параметрически и неявно.

Неявно. Под неявным заданием функции понимают задание функции в виде уравнения F(x; y)=0 (1) неразрешённого относительно у. Производная неявно заданной функции находится путём дифференцирования пох обеих частей выражение 1. Затем y’ выражаем через у и х.

Параметрически.Пусть зависимость между аргументом и функцией задана параметрически в виде 2 уравнений в системе: 1) x=x(t); 2) y=y(t), где t – вспомогательная переменная, называемая параметром. Найдём производную y_x’: t_x’=1/x_t’ (обратная функция). Функцию y=f(x) можно рассматривать как сложную функцию y=y(t), где t=φ(x). По правилу дифференцирования сложной функции имеем: y_x’=y_t’*t_x’. В итоге получаем: y_x’=y_t’*1/x_t’, т.е. y_x’=y_t’/x_t’

Билет 22.Теоремы Ферма, Роля, Лагранжа и Коши. Геометрический смысл.

Точка х0 называется точкой локального минимума (максимума) ф. y=f(x), если для всех х из некоторой окрестности точки х0 выполняется неравенство: f(x)>=f(x0) (f(x)<=f(x0)). Максимум и минимум называются экстремумами функции.

Теорема Ферма.Пусть y=f(x) непрерывна на [a;b] и диф. на (a;b) и пусть точка х0 из (a; b) – точка локального максимума функции f(x). Тогда f ’(x0) = 0.

Геометрический смысл:

В точках локального экстремума касательная к графику функции параллельна оси Ох.

Теорема Роля.Пусть функция y=f(x) непрерывна на отрезке АВ и диф. во всех внутренних

точках (a; b) и f(a)=f(b). Тогда найдётся хотя бы 1 точка из этого интервала, что f ’(x0)=0.

Доказательство:

По свойству функции непрерывной на отрезке найдутся точки х1 и х2 такие, что m=f(x1)<=f(x)<=f(x2)=M для всех х из этого отрезка. Пусть обе точки попадают на концы отрезка x (- [a; b]. x1=a, x2=b è f(a)=f(b)=f(x). Тогда m=M и f(x)=m=M=const для любого х (- [a; b]. Пусть хотя бы 1 из точек x1, x2 попадает внутрь отрезка. Тогда по теореме Фирма производная в этой точке равна 0.

Теорема Коши.

Пусть y=f(x) непрерывна на [a; b] и диф. на (a; b). Аналогично, y=g(x) также непрерывна на [a; b] и диф. на (a; b), но g’(x) ≠ 0 для любого х. Тогда имеет место следующее утверждение: найдётся точка ξ (- (a;b) такая, что (f ‘(b) – f ‘(a))/(f(b) - f(a)) = f ‘(ξ)/g’(ξ)

Теорема Лагранжа.Пусть f(x) непрерывна на [a; b] и диф. на (a; b). Тогда найдётся точка ξ (- (a;b) такая, что f(b) – f(a) = f(ξ)(b-a)

Доказательство:

Возьмём g(x) = x. По теореме Коши найдётся ξ (- (a;b) такая, что (f(b)-f(a)) / (b-a) = f ‘(ξ)

Геометрический смысл:

Билет 23.Раскрытие неопределенностей по правилу Лопиталя.

Определение. Пусть функции f(x) и g(x) диф. в некоторой окрестности точки b. Одновременно являются б.м. или б.б. в т. b и пусть существует lim f ‘(x)/g’(x) (xàb). Тогда существует lim f(x)/g(x) (xàb) = lim f ‘(x)/g’(x).

Доказательство:

Применим к функциям f(x) и g(x) теорему Коши для отрезка [x0; x], лежащего в окрестности точки х0. Тогда f(x)-f(x0)/g(x)-g(x0) = f ‘(c)/g’(c). Учитывая что f(x0) и g(x0) = 0 получаем формулу. И при xà x0 величина х в пределе также стремится к х0.

Замечания:

1) Формула верна только справа налево

2) lim f(x)/g(x) ≠ lim (f(x)/g(x))’

3) Предел отношения функции может существовать, даже если не существует предела отношения производных

4) Правило Лопиталя применяется для раскрытия неопределённостей вида 0/0, беск/беск итд.

Билет 24.Монотонность функции на промежутке. Достаточное условие монотонности. Локальный экстремум. Необходимое условие экстремума. 1-е и 2-е достаточные условия экстремума. Исследование функции на монотонность и экстремум.

Определение.Функция монотонна на промежутке Х, если она возрастает (убывает) на всём промежутке.

Достаточное условие монотонности.Пусть для всех х (- Х f ‘(x)>0 (f’(x)<0). Тогда на Х функция возрастает (убывает)

Доказательство:

x1, x2 (- X, x1<x2. Тогда по теореме Лагранжа найдётся ξ (- (x1; x2) такая, что f(x2)-f(x1) = f ‘(ξ)(x2-x1). x2>x1 è f(x2)>f(x1)

Локальные экстремумы.Точка х0 называется точкой максимума функции y=f(x), если существует такая δ-окрестность точки х0, что для всех х ≠ х0 из этой окрестности выполняется неравенство: f(x)<f(x0). Максимум и минимум – точки экстремума. Функция может иметь экстремум лишь во внутр. точках.

Необходимое условие экстремума.Пусть функция y=f(x) диф. на Х и имеет во внутренней точке этого промежутка локальный максимум. Тогда f ‘(x0) = 0.

Доказательство: по теореме Фирма.

1ое достаточное условие экстремума.Пусть х0 – критическая точка функции f(x) и пусть f(x) диф. в некоторой проколотой окрестности Uε точки х0. Пусть далее в этой окрестности f ‘(x) больше 0 при х<x0 и f ‘(x)<0 при х>x0. Тогда х0 – точка локального максимума.

2ое достаточное условие экстремума.Пусть функция f(x) дважды непрерывна, диф. в некоторой окрестности стационарной т. х0, т.е. f ’(x0) = 0. Тогда если f ‘’(x0)>0, x0 – точка локального минимума, а если <0 – максимума.

Исследование функции на монотонность и экстремум.

1) Найти производную f ‘(x) и крит. точки

2) Найти знак производной на всех интервалах D(y), разбив крит. точки и соответствующие промежутки монотонности

3) Найти точки экстремума и значение ф. в этих точках

Билет 25.Наибольшее и наименьшее значения функции на отрезке: схема нахождения и пример.

Теорема. Пусть функция y=f(x) непрерывна на отрезке [A; B] и диф. на (a; b). Тогда наиб. и наим. значения функции f(x) на [a; b] могут достигаться только в точках локального экстремума или на концах отрезка

Схема нахождения.

1) Находим крит. точки, стационарные точки.

2) Находим значения функции в этих точках и на концах отрезка

3) Выбираем наиб. и наим. значения

Билет 26.Выпуклость, вогнутость функции – геометрическое и аналитическое определения. Точка перегиба. Необходимое и достаточное условия выпуклости (вогнутости) функции. Достаточное условие перегиба.

Кривая называется выпуклой (вогнутой) на (a; b), если для всех точек этого интервала касательная лежит выше (ниже) точек кривой за исключением точки касания.

Геометрическое определение.Функция называется выпуклой (вогнутой) на (a; b), если на этом интервале её график является выпуклой (вогнутой) кривой.

Аналитическое определение.Функция y=f(x) называется выпуклой (вогнутой) на (a; b), если для любых х1, х2 из этого интервала (х1<x2) выполняется неравенство: f((x1+x2)/2) > (f(x1)+f(x2))/2 (для вогнутой первое выражение с – и <)

Достаточное условие выпуклости.Пусть y=f(x) дважды непрерывна и диф. на (a; b) и f ‘’(x)>0 (f ‘’(x)<0) для любого х из этого интервала. Тогда f(x) вогнута (выпукла) на (a; b)

Перегиб.Точка х0 называется точкой перегиба функции или графика функции y=f(x), если в этой точке график меняет своё направление выпуклости.

Достаточное условие перегиба.Пусть f(x) определена в некоторой окрестности точки х0 и дважды непрерывна и диф. в проколотой окрестности этой точки. Пусть в т. f ‘’(x) меняет свой знак. Тогда х0 – точка перегиба f(x).

Доказательство:

Пусть f ‘’(x)<0 слева и f ‘’(x)>0 справа от т. х0. Тогда функция выпукла слева и вогнута справа от т. х0. Тогда х0 – точка перегиба по определению.