Исследование функции на экстремум с помощью

Производных высших порядков

Пусть в точке х = х₁ f¢(x₁) = 0 и f¢¢(x₁) существует и непрерывна в некоторой окрестности точки х₁.

Теорема. Если f¢(x₁) = 0, то функция f(x) в точке х = х₁ имеет максимум, если f¢¢(x₁)<0 и минимум, если f¢¢(x₁)>0.

Выпуклость и вогнутость кривой

Точки перегиба

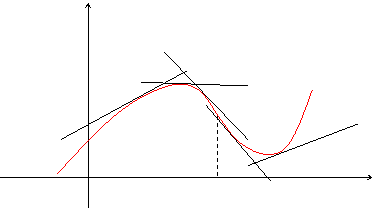
Определение. Кривая обращена выпуклостью вверх на интервале (а, b), если все ее точки лежат ниже любой ее касательной на этом интервале. Кривая, обращенная выпуклостью вверх, называется выпуклой, а кривая, обращенная выпуклостью вниз – называется вогнутой.

у

x

На рисунке показана иллюстрация приведенного выше определения.

Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, то кривая y = f(x) обращена выпуклостью вверх (выпукла).

Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная пересекает кривую.

Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.

Асимптоты

При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.

Определение. Прямая называется асимптотойкривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.

Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.

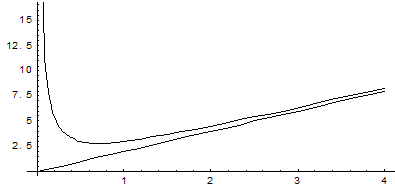
Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции 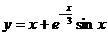. Ее наклонная асимптота у = х.

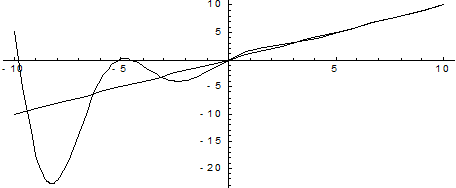
Рассмотрим подробнее методы нахождения асимптот кривых.

Вертикальные асимптоты

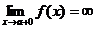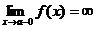Из определения асимптоты следует, что если или или 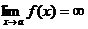, то прямая х = а – асимптота кривой y = f(x).

Например, для функции 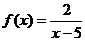прямая х = 5 является вертикальной асимптотой.

Наклонные асимптоты

Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.

M

j

N

j P

Q

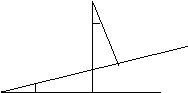
Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N.

Тогда MQ = y – ордината точки кривой, NQ = - ордината точки N на асимптоте.

По условию: 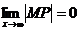, ÐNMP = j, .

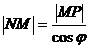Угол j - постоянный и не равный 90⁰, тогда

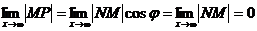
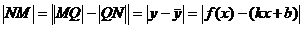
Тогда .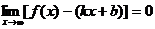

Итак, прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.

В полученном выражении выносим за скобки х:

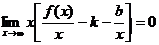
Т.к. х®¥, то 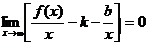, т.к. b = const, то .

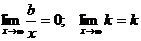Тогда 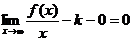, следовательно,

.

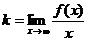Т.к. 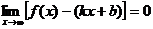, то 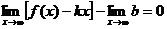, следовательно,

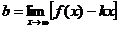
Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.

Пример. Найти асимптоты и построить график функции .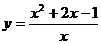

1) Вертикальные асимптоты: y®+¥ x®0-0: y®-¥ x®0+0, следовательно, х = 0- вертикальная асимптота.

2) Наклонные асимптоты:

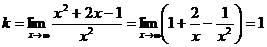
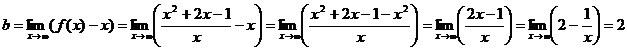
Таким образом, прямая у = х + 2 является наклонной асимптотой.

Построим график функции:

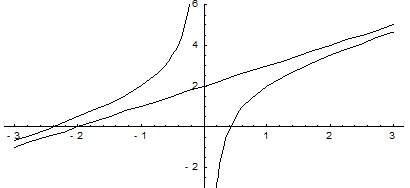
Пример. Найти асимптоты и построить график функции .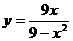

Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.

Найдем наклонные асимптоты: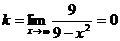

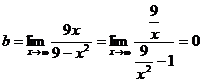
y = 0 – горизонтальная асимптота.

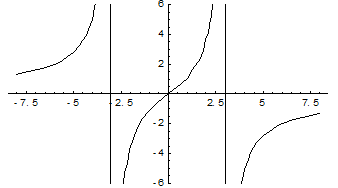
Пример. Найти асимптоты и построить график функции .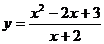

Прямая х = -2 является вертикальной асимптотой кривой.

Найдем наклонные асимптоты.

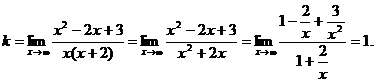
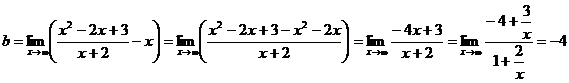
Итого, прямая у = х – 4 является наклонной асимптотой.

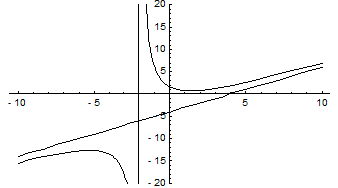
Схема исследования функций

Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:

1) Область существования функции.

Это понятие включает в себя и область значений и область определения функции.

2) Точки разрыва. (Если они имеются).

3) Интервалы возрастания и убывания.

4) Точки максимума и минимума.

5) Максимальное и минимальное значение функции на ее области определения.

6) Области выпуклости и вогнутости.

7) Точки перегиба.(Если они имеются).

8) Асимптоты.(Если они имеются).

9) Построение графика.

Применение этой схемы рассмотрим на примере.

Пример. Исследовать функцию 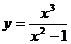и построить ее график.

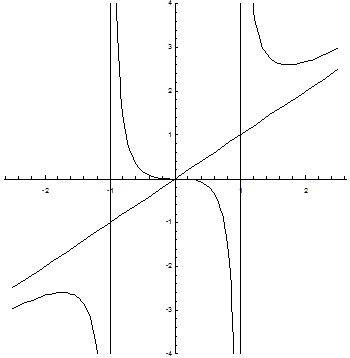
Находим область существования функции. Очевидно, что областью определения функции является область (-¥; -1) È (-1; 1) È (1; ¥).

В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой.

Областью значений данной функции является интервал (-¥; ¥).

Точками разрыва функции являются точки х = 1, х = -1.

Находим критические точки.

Найдем производную функции

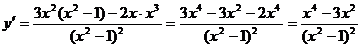
Критические точки: x = 0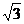; x = - ; x = 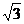; x = -1; x = 1.

Найдем вторую производную функции

.

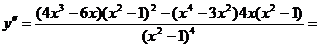
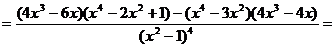
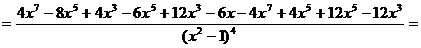
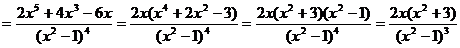Определим выпуклость и вогнутость кривой на промежутках.

-¥ < x < - 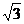, y¢¢ < 0, кривая выпуклая

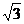- < x < -1, y¢¢ < 0, кривая выпуклая

-1 < x < 0, y¢¢ > 0, кривая вогнутая

0 < x < 1, y¢¢ < 0, кривая выпуклая

1 < x < 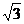, y¢¢ > 0, кривая вогнутая

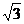< x < ¥, y¢¢ > 0, кривая вогнутая

Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.

-¥ < x < - 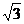, y¢ > 0, функция возрастает

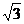- < x < -1, y¢ < 0, функция убывает

-1 < x < 0, y¢ < 0, функция убывает

0 < x < 1, y¢ < 0, функция убывает

1 < x < 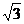, y¢ < 0, функция убывает

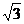< x < ¥, y¢¢ > 0, функция возрастает

Видно, что точка х = - 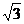является точкой максимума, а точка х = 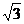является точкой минимума. Значения функции в этих точках равны соответственно -3 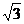/2 и 3 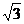/2.

Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.

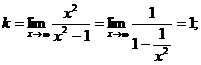
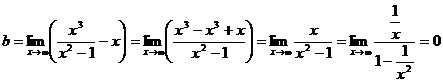
Итого, уравнение наклонной асимптоты – y = x.

Построим график функции: