Косвенные измерения

При косвенных измерениях значение искомой величины находят по результатам прямых измерений других величин, с которыми измеряемая величина связана функциональной зависимостью. Пример косвенных измерений – измерение удельного сопротивления проводника 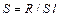по результатам измерения его сопротивления 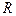, площади поперечного сечения 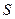и длины .

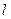В общем случае при косвенных измерениях имеет место нелинейная зависимость между измеряемой величиной 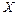и её аргументами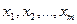

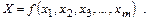(3.19)

Если каждый из аргументов 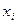характеризуется своей оценкой 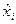и погрешностью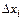

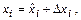
то (3.19) запишется в следующем виде:

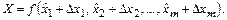(3.20)

Выражение (3.20) можно разложить в ряд Тейлора по степеням :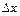

,

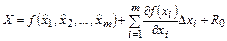где 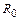- остаточный член ряда.

Из этого выражения можно записать абсолютную погрешность измерения X

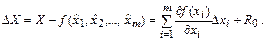(3.21)

Если принять R₀ =0, что справедливо при малых погрешностях аргументов (Dx_i®0), то получаем линейное выражение для погрешности измерения. Такая операция называется линеаризацией нелинейного уравнения (3.19). В получаемом в этом случае выражении для погрешности 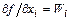- коэффициенты влияния, а W_iDx_i – частные погрешности.

Пренебречь остаточным членом при оценке погрешности допустимо не всегда, т.к. в этом случае оценка погрешности оказывается смещенной. Поэтому, когда связь между X и x_i в выражении (3.19) нелинейная, проверяют допустимость линеаризации по следующему критерию

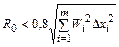, (3.22)

где в качестве остаточного члена берут член ряда второго порядка

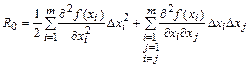
. (3.23)

Если известны границы погрешностей аргументов 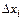(случай наиболее часто встречающийся при однократных измерениях), то легко определить максимальную погрешность измерения X:

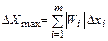. (3.24)

Эту оценку обычно принимают при однократных измерениях и числе аргументов меньше 5.

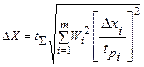При большем числе аргументов прибегают к вероятностному суммированию, т.к. оценка (3.24) оказывается для большинства случаев завышенной. В этом случае

, (3.25)

где t_S и 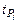- доверительные коэффициенты для распределений общей погрешности и погрешности аргументов, соответствующие своим вероятностям.

При нормальном распределении всех аргументов и одинаковых доверительных вероятностях, выражение (3.25) упрощается

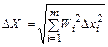. (3.26)

Обычно, особенно при однократных измерениях, законы распределения аргументов неизвестны, а вид суммарного распределения определить практически невозможно, учитывая трансформацию законов распределения при нелинейной связи измеряемой величины X и её аргументов. В этом случае в соответствии с методом ситуационного моделирования принимают закон распределения аргументов равновероятным. При этом доверительная граница 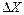погрешности результата косвенного измерения определится по формуле

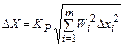, (3.27)

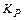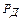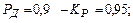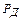где зависит от выбранной вероятности , числа слагаемых и соотношения между ними. Для равных по величине слагаемых и для =0,95 - 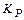=1,1; для 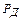=0,99 - 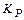=1,4.

Погрешности результатов измерения аргументов могут быть заданы не границами, а параметрами систематических и случайных составляющих погрешностей – границами и СКО. В этом случае оценивают отдельно систематическую и случайную составляющие погрешности косвенного измерения, а затем объединяют полученные оценки.

Что касается суммирования систематических погрешностей (или их неисключенных остатков), то оно осуществляется в зависимости от наличия сведений о распределении погрешностей с использованием выражений (3.24) - (3.27), в которых вместо погрешностей измерений аргументов следует подставить соответствующие границы для систематических погрешностей .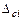

Случайные погрешности результатов косвенных измерений суммируются следующим образом.

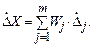Погрешность результата косвенного наблюдения, имеющего случайные погрешности аргументов D j будет равна

Определим дисперсию этой погрешности

;

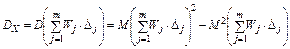т.к. последнее слагаемое равно нулю, то

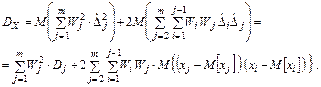(3.28)

В этом выражении 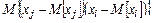- ковариационная функция (корреляционный момент), равный нулю, если погрешности аргументов независимы друг от друга.

Вместо ковариационной функции часто пользуются коэффициентом корреляции

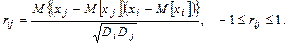(3.29)

В этом случае дисперсия результата наблюдения будет иметь вид 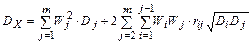. (3.30)

Для получения дисперсии результата измерения необходимо разделить это выражение на число измерений n.

В этих выражениях r_ij – коэффициенты попарной корреляции между погрешностями измерений. Если r_ij = 0, то второе слагаемое в правой части (3.30) равно нулю и общее выражение для погрешности упрощается. Значение r_ij либо известно априорно (в случае однократных измерений), либо (для многократных измерений) его оценка определяется для каждой пары аргументов x_i и x_j по формуле

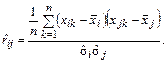
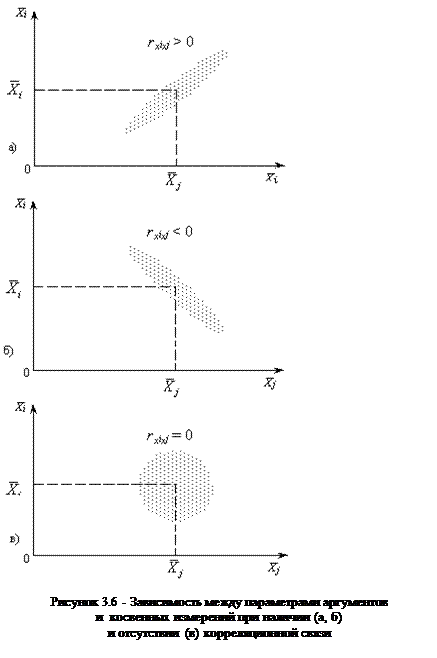
Наличие корреляционной связи между погрешностями аргументов имеет место в том случае, когда аргументы измеряются одновременно, однотипными приборами, находящимися в одинаковых условиях. Причиной возникновения корреляционной связи является изменение условий измерения (пульсации напряжения питающей сети, переменные наводки, вибрации и т.д.). О наличии корреляции удобно судить по графику, на котором изображены пары последовательно получаемых результатов измерений величин x_i и x_j (рис. 3.6).

При малом числе наблюдений может оказаться, что r_ij ¹0 даже при отсутствии корреляционной связи между аргументами. В этом случае необходимо пользоваться числовым критерием отсутствия корреляционной связи, который состоит в выполнении неравенства

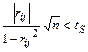, (3.31)

где 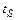- коэффициент Стьюдента для заданной вероятности и числа измерений 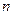(табл. А5).

Границы случайной погрешности после определения оценки дисперсии результатов измерения определяются по формуле

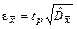, (3.42)

Рисунок 3.6. Зависимость между параметрами аргументов и косвенных измерений при наличии (а , б) и отсутствии корреляционной связи (в).

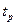где при неизвестном результирующем распределении берется из неравенства Чебышева

.

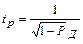Неравенство Чебышева дает завышенную оценку погрешности результата измерений. Поэтому, когда число аргументов больше 4, распределение их одномодальны и среди погрешностей нет резко выделяющихся, число измерений, выполненных при измерении всех аргументов превышает 25-30, то 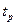определяется из нормированного нормального распределения для доверительной вероятности .

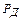Трудности возникают при меньшем числе наблюдений. В принципе можно было бы воспользоваться распределением Стьюдента, но неизвестно как в этом случае определить число степеней свободы. Точного решения эта задача не имеет. Приближенную оценку числа степеней свободы, называемую эффективной, можно найти по формуле, предложенной Б. Уэлчем

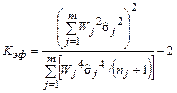. (3.33)

Имея 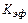и заданную вероятность 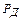можно найти по распределению Стьюдента 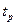и, следовательно, .

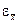Если при разложении в ряд Тейлора необходимо учитывать члены второго порядка, то дисперсию результата наблюдения следует определять по формуле

.

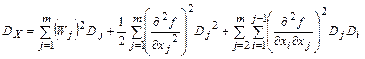Границы суммарной погрешности измерений оценивают аналогично тому, как это было сделано для случая прямых измерений.

В общем случае, при многократных косвенных измерениях статистическая обработка результатов сводится к выполнению следующих операций:

1) из результата наблюдений каждого аргумента исключаются известные систематические погрешности;

2) проверяют, соответствует ли распределение групп результатов каждого аргумента заданному закону распределения;

3) проверяют наличие резко выделяющихся погрешностей (промахов) и исключают их;

4) вычисляют оценки аргументов и параметры их точности;

5) проверяют отсутствие корреляции между результатами наблюдений аргументов попарно;

6) вычисляют результат измерений и оценки параметров его точности;

7) находят доверительные границы случайной погрешности, неисключенную систематическую погрешность и общую погрешность результата измерения.

Алгоритм обработки результатов косвенных измерений приведен на рис. 3.7.