Виды дисперсий и правило их сложения
Виды показателей вариации и порядок их расчета.
Средняя величина погашает индивидуальные различия значений признака. Измерение вариации (колеблемости) признаков дополняет характеристику совокупности и имеет практическое и теоретическое значение. В статистике используют следующие показатели вариации: размах вариации, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации - это разность между максимальным и минимальным размером значения признака ( 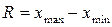 ). Недостаток этого показателя в том, что он не измеряет вариацию внутри совокупности.
). Недостаток этого показателя в том, что он не измеряет вариацию внутри совокупности.
Дисперсия - это средняя из квадратов отклонений от средней величины.
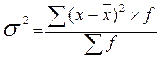
Свойства дисперсии:
Первое свойство. При вычитании из всех значений признака постоянной величины A дисперсия не изменяется.
Второе свойство. При сокращении всех значений признака на постоянный множитель K дисперсия уменьшится в K2 раз.
Третье свойство. Дисперсия признака равна разности между средним квадратом значений признака и квадратом их средней, т.е. 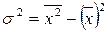 , где
, где 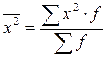 ,
, 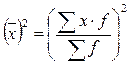 .
.
Используя второе свойство дисперсии можно значительно упростить расчет дисперсии по формуле:
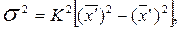 ,
,
Где 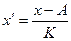 ;
;
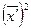 - момент второго порядка;
- момент второго порядка;
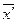 - момент первого порядка.
- момент первого порядка.
Для расчета дисперсии по условию примера 4 используем расчетную таблицу (табл. 2).
Таблица 2
| Заработная плата, д.е. | Число рабочих 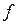 | 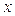 | 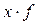 | 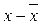 | 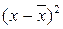 | 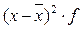 | 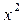 | 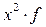 | 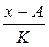 | 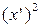 | 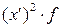 |
| до 250 250-275 275-300 300-325 325 и более | 237,5 262,5 287,5 312,5 387,5 | 2375,0 3937,5 5175,0 3750,0 1687,5 | -44,58 -19,58 5,42 30,42 55,42 | 1987,4 383,4 29,38 925,38 3071,37 | 19874,1 5750,6 528,8 11104,5 15356,8 | 56406,2 68906,2 82656,2 97656,3 | -2 -1 +1 +2 | ||||
| Итого | 16925,0 | 52614,7 |
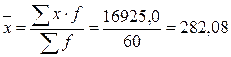 ;
;
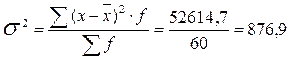 ;
;
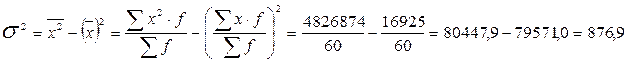
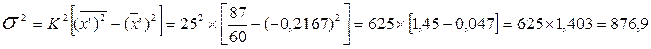
Как видим, расчет по всем формулам дал одинаковый результат. Однако расчет по «способу моментов» менее трудоемок. Дисперсия не имеет единицы измерения.
Виды дисперсий и правило их сложения.
Всякая совокупность, состоящая из значительного числа единиц, может быть расчленена по тому или иному признаку на части, которые называют частными совокупностям или группами.
Совокупность, состоящую из нескольких групп, называют общей.
Для общей и частной совокупностей могут быть определены средние величины и дисперсии, которые соответственно называются общими и групповыми.
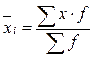
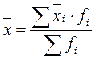 ,
,
где 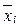 - групповая средняя;
- групповая средняя;
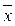 - общая средняя;
- общая средняя;
х - индивидуальные значения признака;
f - число единиц, обладающих данным значением признака;
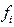 - численность единиц в группе.
- численность единиц в группе.
Общая дисперсия отражает вариацию признака за счет всех условий и причин, действующих в совокупности. Она равна среднему квадрату отклонений отдельных значений признака х от общей средней 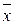 .
.
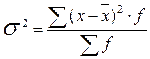
Групповая (частная) дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы (групповой средней).
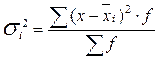
Групповая дисперсия отражает вариацию признака только за счет условий и причин, действующих внутри группы.
Средняя из групповых (частных) дисперсий - это средняя взвешенная из групповых дисперсий (или остаточная):
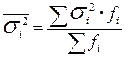 .
.
Средняя из групповых дисперсий не равна общей дисперсии, т.к. она не учитывает колеблемости признака между группами.
Поскольку групповые средние ( 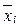 ) являются варьирующей величиной, то может быть определена их дисперсия.
) являются варьирующей величиной, то может быть определена их дисперсия.
Межгрупповая дисперсия характеризует вариацию результативного признака за счет группировочного признака. Она равна среднему квадрату отклонений групповых средних ( 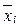 ) от общей средней (
) от общей средней ( 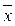 )
)
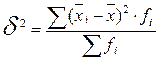 .
.
Между общей, средней из групповых и межгрупповой дисперсиями существует следующая зависимость:
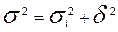 , т. е. общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии. Это соотношение называют правилом сложения дисперсий.
, т. е. общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии. Это соотношение называют правилом сложения дисперсий.
Достоверность правила сложения дисперсий покажем на примере.
Имеются следующие данные о выполнении норм выработки рабочими участка:
| Группы рабочих | Выполнение норм выработки, % | ||||||||
| до | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 | и выше | Итого | |
| Окончившие ПТУ Не прошедшие обучение | - | - | - | ||||||
| Итого |
Для расчета средних величин и дисперсий используем способ «моментов»(см. табл.3).
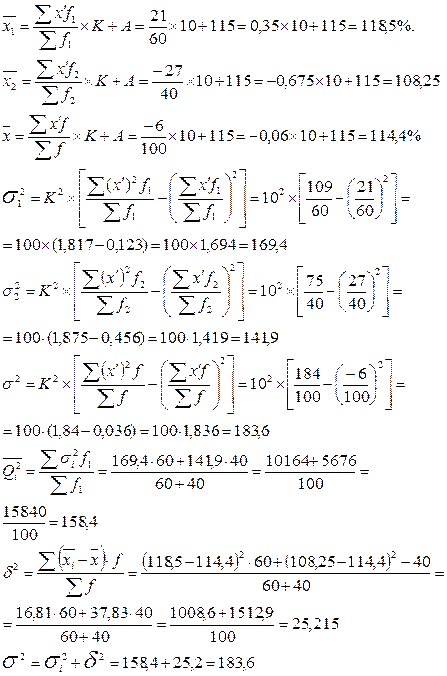
Таблица 3
Расчетная таблица
| Выполнение норм выработки, % | Серединное значение, ( 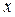 ) ) | Число рабочих | х-А А=115 | x-A K K=10 (х’) | 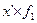 | 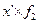 | 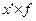 | 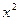 | 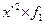 | 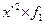 | 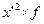 | ||
Окончивших ПТУ 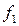 | Не прошедших обучение 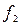 | всего 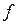 | |||||||||||
| до 90 90-100 100-110 110-120 120-130 130-140 140-150 150 и более | - | - - | -30 -20 -10 +10 +20 +30 +40 | -3 -2 -1 +1 +2 +3 +4 | -4 -14 +11 +12 +12 +4 | -9 -10 -16 +4 +4 | -9 -14 -30 +15 +16 +12 +4 | ||||||
| Итого | -27 | -6 |
Определение ошибки выборочной средней.
Средняя величина признака в генеральной совокупности будет определена по следующей формуле:
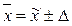 ,
,
где 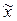 - средняя величина признака в выборочной совокупности;
- средняя величина признака в выборочной совокупности;
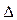 - предельная ошибка выборки.
- предельная ошибка выборки.
В математической статистике доказано, что 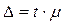 , где t - коэффициент доверия, зависящий от значения вероятности Р и определяемый по таблице значений P(t);
, где t - коэффициент доверия, зависящий от значения вероятности Р и определяемый по таблице значений P(t); 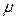 - средняя ошибка.
- средняя ошибка.
При вероятности Р=0,683 значение t=1;
при Р=0,954 t=2;
при Р=0,997 t=3.
Для собственно случайной и механической выборки средняя ошибка при повторном отборе вычисляется по формуле:
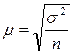
где 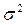 - дисперсия количественного признака, определяемая по формуле:
- дисперсия количественного признака, определяемая по формуле:
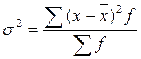 или
или 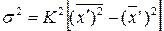 ,
,
n – число единиц выборочной совокупности.
При бесповторном отборе 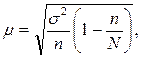
где N – численность генеральной совокупности.
Средняя ошибка выборки для типической и серийной выборки рассчитывается по тем же формулам с той лишь разницей, что:
1) при типической выборке используется средняя из групповых дисперсий:
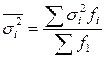 ,
,
где 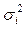 - групповая дисперсия;
- групповая дисперсия;
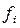 - число единиц в группе.
- число единиц в группе.
2) При серийной выборке – межгрупповая дисперсия:
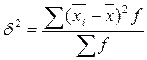 ,
,
где 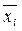 - групповая средняя
- групповая средняя 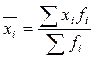
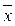 - общая средняя.
- общая средняя.
Кроме того, при серийном отборе формула средней ошибки выборки имеет следующий вид:
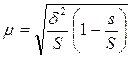 ,
,
где s – число серий в выборке;
S – число серий в генеральной совокупности.
3. Определение ошибки выборочной доли.
Доля единиц, обладающих тем или иным признаком в генеральной совокупности
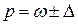 ,
,
где 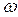 - доля единиц, обладающих данным признаком в выборочной совокупности;
- доля единиц, обладающих данным признаком в выборочной совокупности;
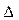 - предельная ошибка выборочной доли.
- предельная ошибка выборочной доли.
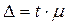 ,
,
где 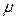 - средняя ошибка выборочной доли.
- средняя ошибка выборочной доли.
Средняя ошибка выборочной доли определяется по следующим формулам:
1) для собственно случайной выборки:
при повторном отборе: 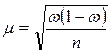 ;
;
при бесповторном отборе: 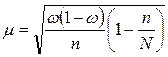 ;
;
2) для механической выборки: 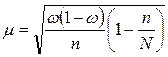 ;
;
3) для типической выборки: 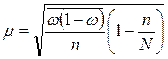 ;
;
4) для серийной выборки 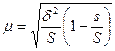
4.Определение необходимой численности выборки
В практике организации выборочного наблюдения возникает потребность определения необходимой численности выборки для обеспечения заданной точности предельной ошибки выборки и ее вероятности. Определение необходимой численности выборки основывается на формуле предельной ошибки выборки.
Из формулы предельной ошибки выборки среднего значения признака при повторном отборе
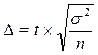
находим 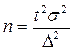 .
.
При бесповторном случайном отборе необходимая численность выборки вычисляется по формуле: 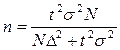 .
.
При типической выборке: 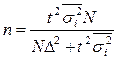 .
.
При серийной выборке 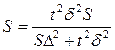 .
.
Необходимая численность выборки при определении доли исчисляется по аналогичным формулам с той разницей, что вместо дисперсии количественного признака, используется дисперсия альтернативного признака.
Так, для случайной бесповторной выборки формула необходимой численности выборки будет иметь следующий вид:
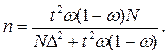
Пример 1
Из 1000 рабочих предприятия в порядке случайной бесповторной выборки обследовано 100 человек, которые по уровню дневной выработки распределились так:
| Дневная выработка (шт.) | 30-40 | 40-50 | 50-60 | 60-70 | Итого |
| Число рабочих |
По этим данным установить:
1) среднюю дневную выработку одного рабочего предприятия с вероятностью 0,954.
2) Долю рабочих предприятия с дневной выработкой 60 штук и более с вероятностью 0,683.
3) Объем выборки, чтобы с вероятностью 0,954 предельная ошибка выборки при определении средней выработки не превышала 2-х штук.
4) Объем выборки, чтобы с вероятностью 0,954 предельная ошибка выборки при определении доли рабочих с дневной выработкой 60 штук и более не превышала 6%.
Решение:
1) 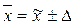
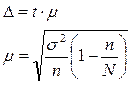
В нашем примере объем выборки (n)=100 рабочих. Численность генеральной совокупности (N) 1000 рабочих.
Для нахождения выборочной средней ( 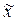 ) и выборочной дисперсии (
) и выборочной дисперсии ( 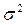 ) составим расчетную таблицу:
) составим расчетную таблицу:
Таблица 4
| Дневная выработка, шт. | Число рабочих (f) | x | x-A (A=45) | 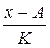 K=10 (x’) K=10 (x’) | 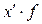 | 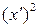 | 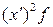 |
| 30-40 40-50 50-60 60-70 | -10 +10 +20 | -1 +1 +2 | -30 +24 +26 | ||||
| Итого | х | х | х |
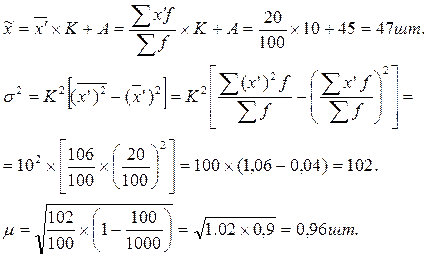
При вероятности 0,954 t=2, тогда 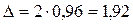 шт.
шт.
С вероятностью 0,954 можно утверждать, что средняя дневная выработка одного рабочего предприятия находится в пределах 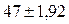 шт.,т.е. будет не меньше 45,08 и не больше 48,92 штук.
шт.,т.е. будет не меньше 45,08 и не больше 48,92 штук.
2) 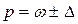
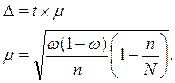

Выборочная доля рабочих с дневной выработкой 60 штук и более по условию задачи равна: 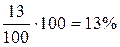 , а выборочная дисперсия доли
, а выборочная дисперсия доли 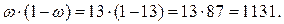
Средняя ошибка доли:
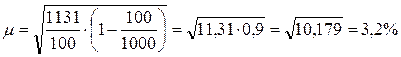 при вероятности 0,683 t=1, тогда
при вероятности 0,683 t=1, тогда 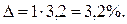
Следовательно, с вероятностью 0,683 можно утверждать, что доля рабочих предприятия с дневной выработкой 60 шт. и более находится в пределах 13 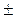 3,2 или от 9,8 до 16,2%.
3,2 или от 9,8 до 16,2%.
3) 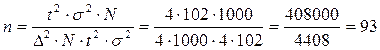 рабочих.
рабочих.
Для того, чтобы предельная ошибка выборки с вероятностью 0,954 (при дисперсии = 102) не превышала 2-х штук, достаточно подвергнуть выборочному обследованию 93 рабочих.
4) 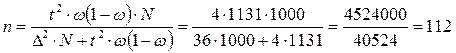 рабочих.
рабочих.
Для того, чтобы предельная ошибка выборки при вероятности 0,954 не превышала 6%, необходимо подвергнуть выборочному обследованию 112 рабочих.
Пример 2
Из 2500 рабочих трёх цехов завода подвергнуто пропорциональному типическому отбору 200 человек, которые по проценту выполнения норм выработки распределились следующим образом:
| Число рабочих по профессиям % выпол- нения норм выработки | Слесари | Токари | Шлифовщики | Итого |
| 90-100 | ||||
| 100-110 | ||||
| 110-120 | ||||
| Итого |
Принимая, что в каждой группе произведена случайная повторная выборка, определить:
1. Возможные пределы среднего процента выполнения норм выработки всеми рабочими завода (с вероятностью 0,954).
2. Возможные пределы доли рабочих, выполняющих нормы выработки не менее чем на 100% (с вероятностью 0,997).
3. Необходимую численность выборки при определении среднего процента выполнения норм выработки, чтобы с вероятностью 0,954, предельная ошибка выборки не превышала 1%.
4. Необходимую численность выборки при определении доли рабочих, выполняющих нормы выработки не менее чем на 100%, чтобы предельная ошибка выборки не превышала 3% (с вероятностью 0,954).
Решение:
1) Средняя ошибка выборочной средней при типической выборке (повторный отбор) исчисляется по формуле:
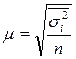
где 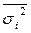 - средняя внутригрупповая дисперсия, равная средней взвешенной из дисперсий отдельных типических групп.
- средняя внутригрупповая дисперсия, равная средней взвешенной из дисперсий отдельных типических групп.
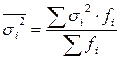
Для нахождения выборочной средней и средней внутригрупповой дисперсии составим расчётную таблицу:
Таблица 5
Расчетная таблица
| % выполнения норм выработки | 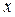 | Число рабочих | 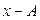 ( ( 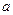 = =105) = =105) | 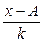 ( ( 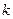 =10) =10) 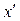 | 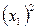 | 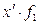 | 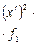 | 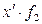 | 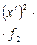 | 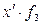 | 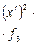 | 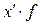 | |||
Слесари 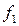 | Тока- ри 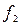 | Шлифов-щики 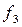 | Итого 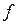 | ||||||||||||
| 90-100 | -10 | -1 | -2 | -20 | -18 | -40 | |||||||||
| 100-110 | |||||||||||||||
| 110-120 | +10 | +1 | +30 | +40 | +40 | +100 | |||||||||
| Итого | x | x |
Определяем выборочную среднюю:
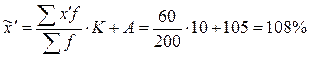
Дисперсии типических групп (внутригрупповые дисперсии) определим по формуле:

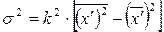
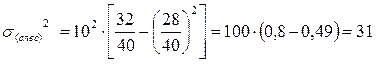
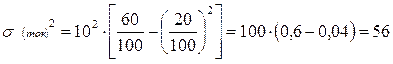
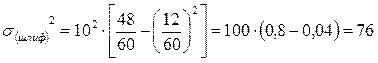


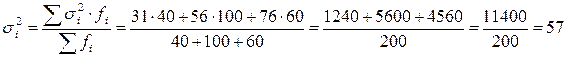
Средняя ошибка выборки будет равна:
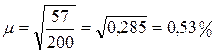
Предельная ошибка выборки составит:
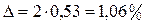 .
.
Следовательно, с вероятностью 0,954 можно утверждать, что средний процент выполнения норм выработки всеми рабочими завода находится в пределах 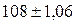 , т.е. от 106,94% до 109,06%.
, т.е. от 106,94% до 109,06%.
2) Выборочная доля
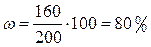
Средняя ошибка выборочной доли при типическом повторном отборе определяется по формуле:
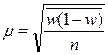
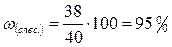 ;
; 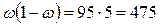
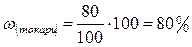 ;
; 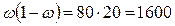
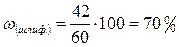 ;
; 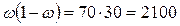
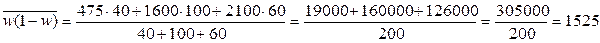
Средняя ошибка доли будет равна:
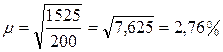 .
.
Тогда предельная ошибка: 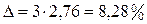 .
.
Следовательно, с вероятностью 0,997, можно утверждать, что доля рабочих завода, выполняющих нормы выработки не менее, чем на 100%, находится в пределах 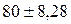 , т. е. от 71,72% до 88,28%.
, т. е. от 71,72% до 88,28%.
3) Объём выборки, обеспечивающий предельную ошибку выборки не более чем 1%, будет равен (с вероятностью 0,954)
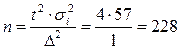 рабочих.
рабочих.
4) Объём выборки при исчислении доли, обеспечивающий предельную ошибку выборки не более чем на 3% (с вероятностью 0,954)
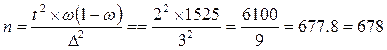 рабочих.
рабочих.
Пример 3
Из 30 бригад (по 10 человек каждая) отобрано 3 бригады, рабочие которых распределились по возрасту следующим образом:
| № бригады | Возраст рабочих (лет) |
| 35, 42, 28, 23, 51, 18, 36, 29, 46, 32 | |
| 18, 24, 49, 32, 54, 43, 27, 38, 51, 26 | |
| 50, 44, 36, 28, 23, 41, 31, 24, 46, 33 |
Определить:
1) с вероятностью 0,683 средний возраст рабочих всех 30 бригад;
2) объём выборки, обеспечивающий с вероятностью 0,997 предельную ошибку выборки, не превышающую 1 года.
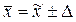
Средний возраст рабочих по каждой бригаде определим по формуле средней арифметической простой, как сумму возрастов всех рабочих бригады, делённую на число рабочих.
Так, средний возраст рабочих первой серии (бр. №5) будет равен
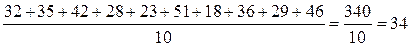 года
года
Аналогичным образом определяем средний возраст рабочих следующих серий:
второй = 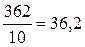 года,
года,
третьей = 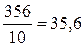 года.
года.
Средний возраст рабочих выборочной совокупности составит 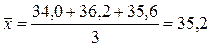 года.
года.
Для серийной выборки
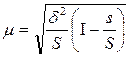 ,
,
где 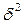 - межгрупповая дисперсия, определяемая по формуле
- межгрупповая дисперсия, определяемая по формуле
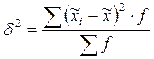 .
.
Поскольку численность всех бригад одинаковая, можно использовать не взвешенную среднюю
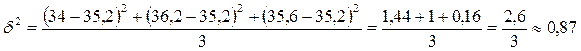
Тогда 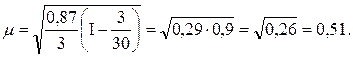
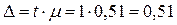 года
года
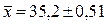 .
.
С вероятностью 0,683 мы можем утверждать, что средний возраст всех рабочих будет не меньше 34,69 года и не больше 35,71 года.
2) 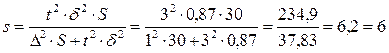 бригад.
бригад.
