Окрестность точки на числовой прямой. Предел функции в точке. Предел в бесконечно удаленной точке. Геометрическая интерпретация предела
1) Окрестность точки на числовой прямой. Предел функции в точке. Предел в
бесконечно удаленной точке. Геометрическая интерпретация предела.
Пусть 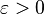 произвольное фиксированное число.
произвольное фиксированное число.
Окрестностью точки 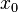 на числовой прямой (иногда говорят
на числовой прямой (иногда говорят  -окрестностью) называется множество точек, удаленных от
-окрестностью) называется множество точек, удаленных от 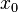 не более чем на
не более чем на  , то есть
, то есть 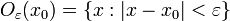 .
.
В многомерном случае роль окрестности выполняет открытый  -шар с центром в точке
-шар с центром в точке 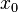 .
.
2) Пусть задано некоторое числовое множество 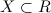 и каждому
и каждому 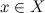 поставлено в соответствие число
поставлено в соответствие число 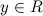 , тогда говорят, что на множестве
, тогда говорят, что на множестве 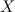 задана функция
задана функция 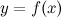 ,
, 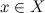 .Число
.Число 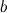 называется пределом функции
называется пределом функции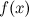 в точке
в точке  , если для
, если для 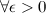
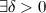 такое, что для
такое, что для 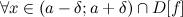 из того, что
из того, что 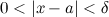 следует, что
следует, что 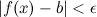 :
: 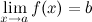 или
или 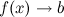 при
при 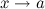 .
.
3) Будем говорить, что переменная x стремится к бесконечности, если для каждого заранее заданного положительного числа M (оно может быть сколь угодно большим) можно указать такое значение х=х0, начиная с которого, все последующие значения переменной будут удовлетворять неравенству |x|>M.
Например, пусть переменная х принимает значения x1= –1, x2=2, x3= –3, …, xn=(–1)nn, … Ясно, что это бесконечно большая переменная величина, так как при всех M > 0 все значения переменной, начиная с некоторого, по абсолютной величине будут больше M.
Переменная величина x → +∞, если при произвольном M > 0 все последующие значения переменной, начиная с некоторого, удовлетворяют неравенству x > M.
Аналогично, x → – ∞, если при любом M > 0 x < -M.
Будем говорить, что функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M, что для всех значений x, удовлетворяющих неравенству |x|>M, выполняется неравенство |f(x) - b| < ε.
Обозначают 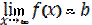
4) Из определения предела следует: если переменная xn имеет пределом число a, то это значит, что как бы мало не было любое наперед заданное положительное число e, всегда можно найти такое значение xN, что все последующие ее значения будут удовлетворять неравенству
|xn - a| < e при n і N (1)
Легко видеть, что неравенство (1) равносильно следующим двум неравенствам:
-e < xn - a < e (2)
В самом деле, если xn - a > 0, то из неравенства xn - a < e имеем |xn - a| < e. Если же xn - a < 0, то из неравенства -e < xn - a имеем|xn - a| < e.
Прибавляя a ко всем частям неравенств (2), получаем два других неравенства, равносильных неравенству (1)
