Второй тип задач: есть изменения массы
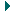 Температуру воздуха в комнате подняли с t1 = 7 °С до t2 = 27 °С. Какая масса воздуха должна выйти из комнаты, чтобы давление осталось неизменным, Р = 105 Па? Объем воздуха в комнате V = 50 м3.
Температуру воздуха в комнате подняли с t1 = 7 °С до t2 = 27 °С. Какая масса воздуха должна выйти из комнаты, чтобы давление осталось неизменным, Р = 105 Па? Объем воздуха в комнате V = 50 м3.
| μ = 0,029кг/моль t1 = 7°C t2 = 27°C Р =105 Па V=50м3 | Т1=280К Т2=300К | Так как при нагревании все тела расширяются, а комната не герметична, следовательно, масса воздуха в комнате при нагревании уменьшается (есть утечка газа), но при этом, понятно, что объем газа не меняется и остается равным объему комнаты. Для каждого состояния газа запишем уравнение Менделеева-Клапейрона, и определим из них массу воздуха в комнате при разной температуре.  |
| ρ-? | 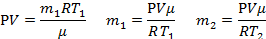 | |
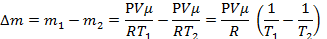 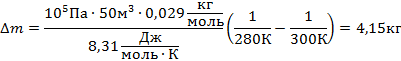 |
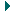 Стеклянная колба закрыта пробкой и взвешена при температуре t1 = 15 °С. Открыв пробку, колбу нагрели до температуры t2 = 80 °С. При следующем взвешивании масса колбы оказалась на m = 0,25 г меньше. Чему равен объем колбы?
Стеклянная колба закрыта пробкой и взвешена при температуре t1 = 15 °С. Открыв пробку, колбу нагрели до температуры t2 = 80 °С. При следующем взвешивании масса колбы оказалась на m = 0,25 г меньше. Чему равен объем колбы?
| μ = 0,029кг/моль t1 = 15°C t2 = 80°C Р =105 Па ∆m=0,25 г | Т1=288К Т2=353К 0,25∙10-3кг | Масса стеклянной колбы не меняется, меняется масса газа в ней, так как есть утечка: при нагревании все тела расширяются, а колба не герметична, следовательно, масса воздуха в ней при нагревании уменьшается, но при этом, понятно, что объем газа не меняется и остается равным объему колбы. Будем считать, что атмосферное давление нормальное. Для каждого состояния газа запишем уравнение Менделеева-Клапейрона, и определим из них массу воздуха в колбе при разной температуре.  |
| V -? | 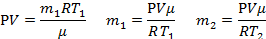 | |
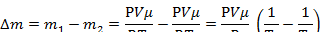 Выразим отсюда объем колбы: Выразим отсюда объем колбы: 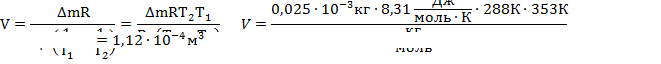 |
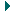 В баллоне емкостью V = 12 л находится азот массой m1 = 1,5 кг при температуре t1 = 37°С. Каким станет давление в баллоне при температуре t2 =50 °С, если выпустить 35% азота? Первоначальное давление считать нормальным.
В баллоне емкостью V = 12 л находится азот массой m1 = 1,5 кг при температуре t1 = 37°С. Каким станет давление в баллоне при температуре t2 =50 °С, если выпустить 35% азота? Первоначальное давление считать нормальным.
| μ = 0,028кг/моль t1 = 37°C t2 = 50°C Р1 =105 Па m2=0,65m1 | Т1=310К Т2=323К | Для каждого состояния газа запишем уравнение Менделеева-Клапейрона. 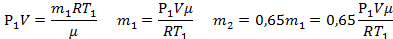 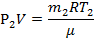 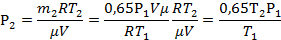 |
| Р2 -? | 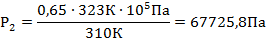 |
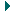 В сосуде объемом V = 1 л находится идеальный газ. В сосуде объемом V = 1 л находится идеальный газ. Сколько молекул газа нужно выпустить из сосуда, чтобы при понижении температуры в k=2 раза его давление уменьшилось в z =4 раза?
В сосуде объемом V = 1 л находится идеальный газ. В сосуде объемом V = 1 л находится идеальный газ. Сколько молекул газа нужно выпустить из сосуда, чтобы при понижении температуры в k=2 раза его давление уменьшилось в z =4 раза?
| μ = 0,028кг/моль t1 = 37°C t2 = 50°C Р1 =105 Па m2=0,65m1 | Т1=310К Т2=323К | Для каждого состояния газа запишем уравнение Менделеева-Клапейрона. 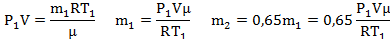 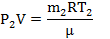 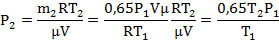 |
| Р2 -? | 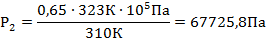 |
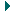 Когда из сосуда выпустили некоторое количество газа, давление в нем упало на 40%, а абсолютная температура на 20%. Какую часть газа выпустили?
Когда из сосуда выпустили некоторое количество газа, давление в нем упало на 40%, а абсолютная температура на 20%. Какую часть газа выпустили?
| T2 = 0,8T1 Р2 =0,6Р1 m2=0,65m1 | Для каждого состояния газа запишем уравнение Менделеева-Клапейрона. 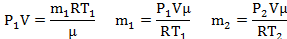 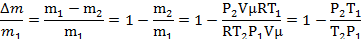 |
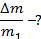 | |
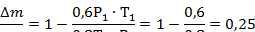 |
 В сосуде объемом V = 0,5 л находится идеальный газ при давлении Р1=1 атм. и температуре t = 27 °С. Сколько молекул газа нужно выпустить из сосуда, чтобы давление в нем уменьшилось в 2 раза? Температура газа не изменяется.
В сосуде объемом V = 0,5 л находится идеальный газ при давлении Р1=1 атм. и температуре t = 27 °С. Сколько молекул газа нужно выпустить из сосуда, чтобы давление в нем уменьшилось в 2 раза? Температура газа не изменяется.
| T = 300К Р=1 атм. =105Па Р1=2Р2 V=0,5л=0,5∙10-3м3 | Для каждого состояния газа запишем уравнение Менделеева-Клапейрона. 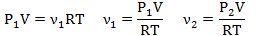  |
| ∆N-? | |
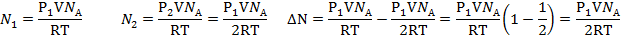 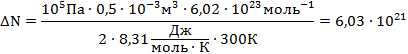 |
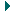 В пустой сосуд объемом V нагнетают воздух при помощи поршневого насоса, объем цилиндра которого V0. Каким будет давление воздуха в сосуде после N качаний?
В пустой сосуд объемом V нагнетают воздух при помощи поршневого насоса, объем цилиндра которого V0. Каким будет давление воздуха в сосуде после N качаний?
| V N V0 | Задачи про насосы решаются так же на основе уравнения Менделеева-Клапейрона. Надо записать уравнение для накаченной массы, то есть той, что поступила в сосуд. И так же записать уравнение Менделеева-Клапейрона для газа, поступающего в рабочий резервуар насоса. И учесть, что вся масса газа, попавшая в сосуд – это масса газа, попадавшая в резервуар насоса N раз. Будем считать, что в насос газ поступает при атмосферном давлении |
| Р-? | |
Запишем уравнение Менделеева-Клапейрона для газа, поступившего в цилиндр насоса: 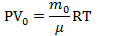 Запишем уравнение Менделеева-Клапейрона для газа, поступившего в сосуд: Запишем уравнение Менделеева-Клапейрона для газа, поступившего в сосуд: 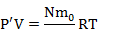 Поделим второе уравнение на первое: Поделим второе уравнение на первое: 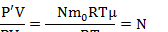 |
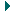 Компрессор засасывает из атмосферы каждую секунду 3 литра воздуха, которые подаются в баллон емкостью 45 литров. Через сколько времени давление в баллоне будет превышать атмосферное в 9 раз? Начальное давление в баллоне равно атмосферному.
Компрессор засасывает из атмосферы каждую секунду 3 литра воздуха, которые подаются в баллон емкостью 45 литров. Через сколько времени давление в баллоне будет превышать атмосферное в 9 раз? Начальное давление в баллоне равно атмосферному.
