Дискретная случайная величина
Случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями называется …
+ дискретная случайная величина
- непрерывная случайная величина
- дисперсия
- закон распределения
- функция распределения
Соответствие между возможными значениями и их вероятностями дискретной случайной величины называется ее …
- средним квадратическим отклонением
- математическим ожиданием
- дисперсией
+ законом распределения
- функцией распределения
Сумма произведений всех возможных значений дискретной случайной величины на соответствующие вероятности называется …
- средним квадратическим отклонением
+ математическим ожиданием
- дисперсией
- законом распределения
- функцией распределения
Математическое ожидание квадрата отклонения дискретной случайной величины от ее математического ожидания называется …
- дискретной случайной величиной
- математическим ожиданием
+ дисперсией
- законом распределения
- функцией распределения
Функция, определяющая вероятность того, что случайная величина Х, в результате испытания примет значение, меньшее, чем х, называется …
- дискретная случайная величина
- математическое ожидание
- дисперсия
- закон распределения
+ функция распределения
Дискретная случайная величина Х задана законом распределения вероятностей
| Х | -1 | |||
| Р | 0,2 | 0,3 | 0,1 | 0,4 |
Тогда значение интегральной функции распределения вероятностей F(2) равно ...
- 0,5
- 1
+ 0,6
- 0,4
Дискретная случайная величина Х задана законом распределения вероятностей
| Х | -1 | |||
| Р | 0,2 | 0,3 | 0,1 | 0,4 |
Тогда значение интегральной функции распределения вероятностей F(0,5) равно ...
+ 0,5
- 1
- 0,6
- 0,4
Дискретная случайная величина Х задана законом распределения вероятностей
| Х | -1 | |||
| Р | 0,2 | 0,3 | 0,1 | 0,4 |
Тогда значение интегральной функции распределения вероятностей F(-0,5) равно ...
- 0,5
- 1
+ 0,2
- 0,4
Функция распределения вероятностей дискретной случайной величины Х имеет вид
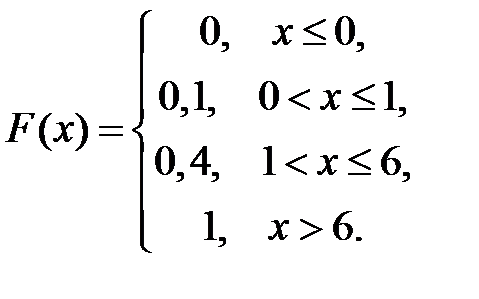
Тогда вероятность 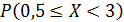 равна …
равна …
- 0,5
+ 0,3
- 0,4
- 0,6
Функция распределения вероятностей дискретной случайной величины Х имеет вид
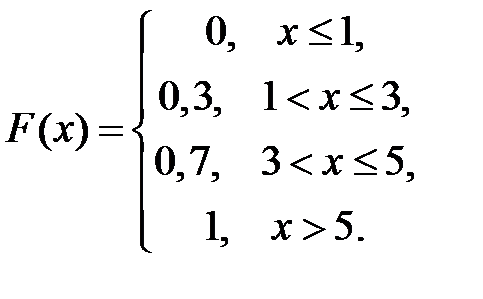
Тогда вероятность 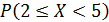 равна …
равна …
- 0,5
- 0,3
+ 0,4
- 0,7
Функция распределения вероятностей дискретной случайной величины Х имеет вид
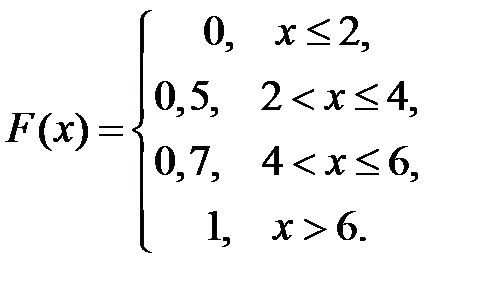
Тогда вероятность 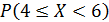 равна …
равна …
- 0,5
- 0,3
- 0,4
+ 0,2
Задан закон распределения дискретной случайной величины
| Х | |||||
| Р | 0,1 | р | 0,35 | 0,35 | 0,1 |
Тогда значение р равна…
+ 1/10
- 1/4
- 1/2
- 1/5
Задан закон распределения дискретной случайной величины
| Х | ||||
| р | 0,2 | 0,3 | р | 0,1 |
Тогда значение р равно…
+ 0,4
- 0,6
- 0,3
- 0,9
Задан закон распределения дискретной случайной величины
| Х | ||||
| р | 0,1 | 0,2 | р | 0,5 |
Тогда значение р равно…
- 0,4
- 0,5
- 0,3
+ 0,2
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | |||
| р | 0,3 | 0,3 | 0,4 |
Тогда ее функция распределения вероятностей имеет вид …
- 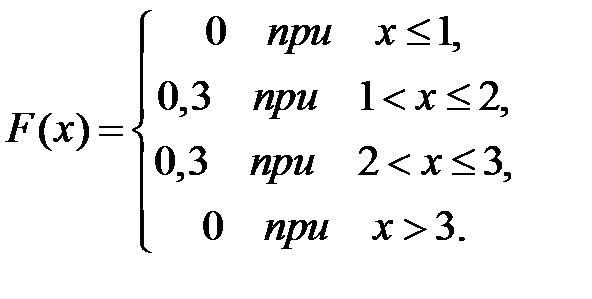
- 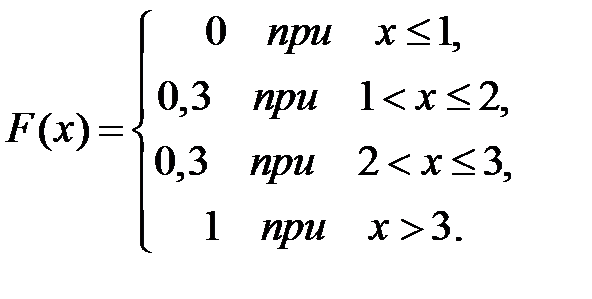
+ 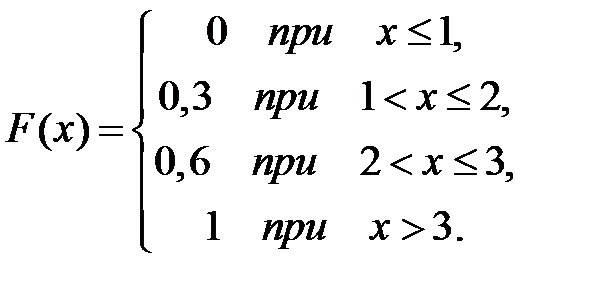
- 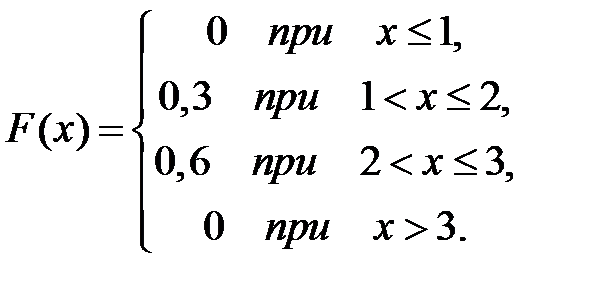
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | |||
| р | 0,2 | 0,5 | 0,3 |
Тогда ее функция распределения вероятностей имеет вид …
- 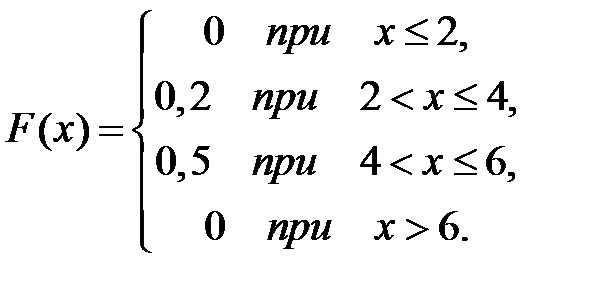
- 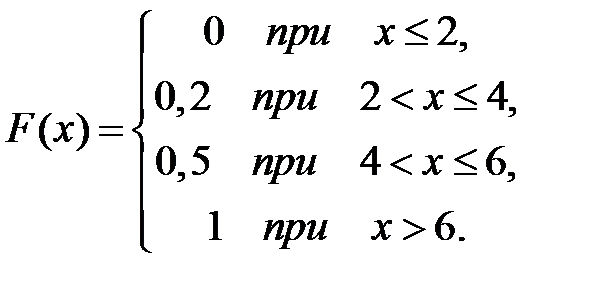
- 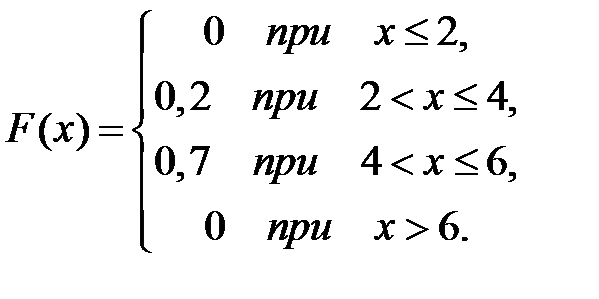
+ 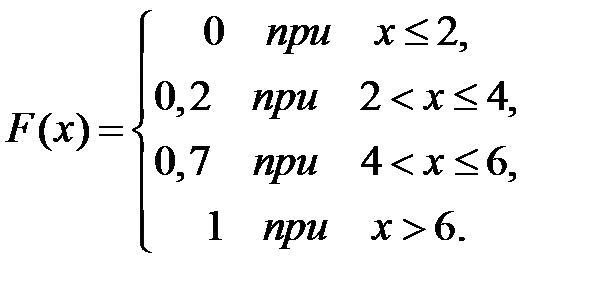
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | |||
| р | 0,5 | 0,3 | 0,2 |
Тогда ее функция распределения вероятностей имеет вид …
- 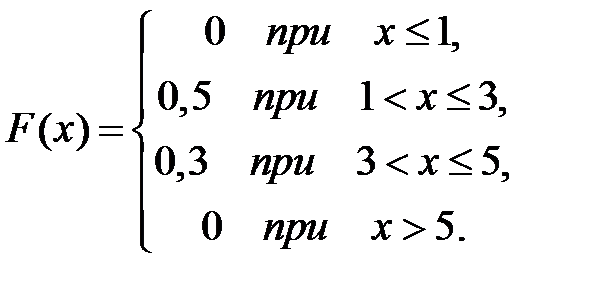
- 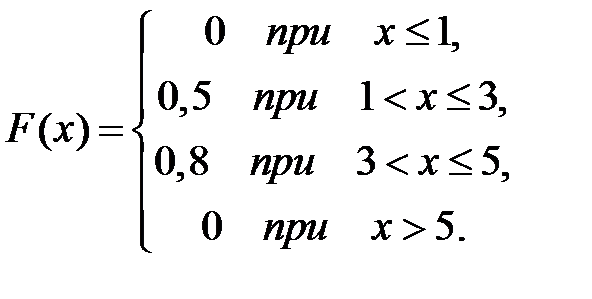
+ 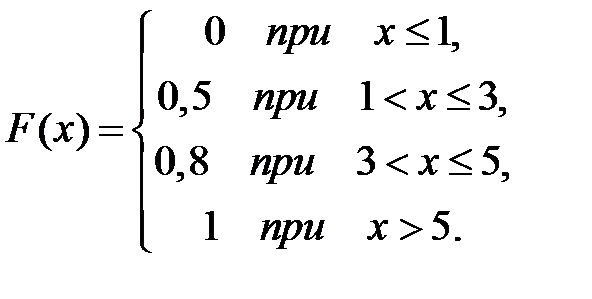
- 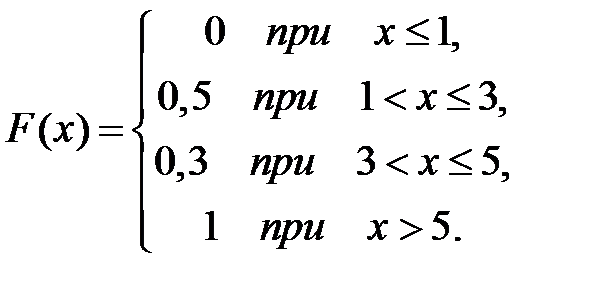
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | ||||
| р | 0,1 | a | b | 0,3 |
Тогда значения a и b могут быть равны …
- a=0,6, b=0,6
- a=0,3, b=0,2
- a=0,3, b=0,1
+ a=0,4, b=0,2
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | ||||
| р | 0,2 | a | b | 0,3 |
Тогда значения a и b могут быть равны …
- a=0,5, b=0,5
+ a=0,3, b=0,2
- a=0,3, b=0,1
- a=0,4, b=0,2
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | ||||
| р | 0,4 | a | b | 0,3 |
Тогда значения a и b могут быть равны …
- a=0,7, b=0,7
- a=0,3, b=0,2
+ a=0,2, b=0,1
- a=0,4, b=0,3
Если к случайной величине Х прибавить постоянную величину 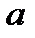 , то
, то 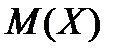
- не изменится
+ увеличится на 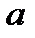 единиц
единиц
- увеличится в 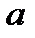 единиц
единиц
- увеличится на 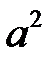 единиц
единиц
Если к случайной величине Х прибавить постоянную величину 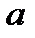 , то
, то 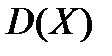
+ не изменится
- увеличится на 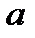 единиц
единиц
- увеличится в 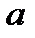 единиц
единиц
- увеличится на 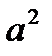 единиц
единиц
Если к случайной величине Х прибавить постоянную величину 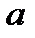 , то
, то 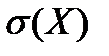
+ не изменится
- увеличится на 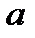 единиц
единиц
- увеличится в 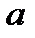 единиц
единиц
- увеличится на 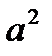 единиц
единиц
Если случайную величину Х умножить на постоянную величину 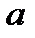 , то
, то 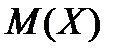
- не изменится
- увеличится на 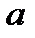 единиц
единиц
+ увеличится в 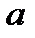 единиц
единиц
- увеличится на 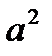 единиц
единиц
Если случайную величину Х умножить на постоянную величину 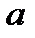 , то
, то 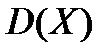
- не изменится
- увеличится на 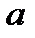 единиц
единиц
- увеличится в 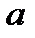 единиц
единиц
+ увеличится в 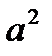 единиц
единиц
Если случайную величину Х умножить на постоянную величину 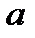 , то
, то 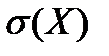
- не изменится
- увеличится на 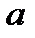 единиц
единиц
+ увеличится в 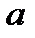 единиц
единиц
- увеличится на 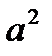 единиц
единиц
Если Х – число появлений события А в 10 испытаниях, где р(А)=р=0,6 то М(Х) и D(Х) принимают значения…
- М(Х) =0, D(Х)=1,2
- М(Х)=3, D(Х)=1,6
- М(Х)=4, D(Х)=1,2
+ М(Х)=6, D(Х)=2,4
Если Х - число появлений события А в 12 испытаниях, где р(А)=р=0,4, то М(Х) и D(Х) принимают значения
- М(Х) =6,1, D(Х) =4,34
+ М(Х)=4,8, D(Х) =2,88
- М(Х)=3,8, D(Х) =2,79
- М(Х)=5,6, D(Х) =3,66
Если Х - число появлений события А в 14 испытаниях, где р(А)=р=0,7, то М(Х) и D(Х) принимают значения
- М(Х) =6,4, D(Х) =5,04
- М(Х)=5,2, D(Х) =2,12
+ М(Х)=9,8, D(Х) =2,94
- М(Х)=2,6, D(Х) =1,52
Дискретная случайная величина Х имеет закон распределения вероятностей:
| Х | ||
| р | 0,3 | 0,7 |
Математическое ожидание этой случайной величины равно…
- 1
- 5
+ 2,7
- 2,3
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | -1 | |
| Р | 0,1 | 0,9 |
Тогда математическое ожидание этой случайной величины равно ...
+ 4,4
- 4,5
- 4,6
- 2
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | -1 | |
| Р | 0,4 | 0,6 |
Тогда математическое ожидание этой случайной величины равно ...
+ 2
- 1,5
- 3
- 2,8
Дискретная случайная величина Х задана законом распределения вероятностей
| Х | -1 | ||
| р | 0,1 | 0,3 | 0,6 |
Тогда математическое ожидание случайной величины Y=4X равно…
- 4
+ 4,4
- 5,2
- 5,1
Дискретная случайная величина Х задана законом распределения вероятностей
| Х | -1 | ||
| р | 0,1 | 0,3 | 0,6 |
Тогда математическое ожидание случайной величины Y=6X равно…
- 18,6
- 8,9
+ 17,4
- 24
Дискретная случайная величина Х задана законом распределения вероятностей
| Х | -1 | ||
| р | 0,1 | 0,3 | 0,6 |
Тогда математическое ожидание случайной величины Y=3X равно…
- 7,5
- 9
- 5,3
+ 6,9
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,54. Тогда математическое ожидание числа появлений этого события равно …
- 9,20
- 4,97
- 10,26
+ 10,8
Вероятность появления события А в 30 независимых испытаниях, проводимых по схеме Бернулли, равна 0,24. Тогда математическое ожидание числа появлений этого события равно …
- 9,20
+ 7,2
- 7,5
- 10,8
Вероятность появления события А в 20 независимых испытаниях, проводимых по схеме Бернулли, равна 0,36. Тогда математическое ожидание числа появлений этого события равно …
- 10,20
- 7,4
- 10,26
+ 7,2
Если Х и Y случайные величины, D(Х)=1, D(Y)=2, а Z=6Х+3Y, то D(Z) равна…
- 12
+ 54
- 42
- 24
Если Х и Y случайные величины, М(Х)=2, М(Y)=3, а Z=7Х+4Y, то М(Z) равна…
+ 26
- 146
- 13
- 5
Если Х и Y, случайные величины, D(Х)=2, D(Y)=3, а Z=6Х-3Y , тогда D(Z) равна…
- 3
- 45
- 21
+ 99
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | х2 | ||
| р | 0,2 | 0,6 | 0,2 |
Если математическое ожидание М(Х)=3,6, то значение х2 равно …
- 4
+ 3
- 5
- 6
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | х1 | ||
| р | 0,3 | 0,4 | 0,3 |
Если математическое ожидание М(Х)=3,2, то значение х1 равно …
- 1
- –1
- 0
+ –2
Дискретная случайная величина Х задана законом распределения вероятностей:
| Х | х3 | ||
| р | 0,5 | 0,1 | 0,4 |
Если математическое ожидание М(Х)=3,4, то значение х3 равно …
- 10
- 7
+ 5
- 6
