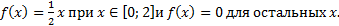Дискретная случайная величина.
В простейшем случае, когда множество исходов опыта конечно, каждому исходу опыта 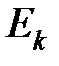 поставлено в соответствие единственное число
поставлено в соответствие единственное число 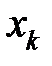 , которое и называется значением случайной величины на исходе
, которое и называется значением случайной величины на исходе 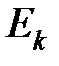 и представляется в виде
и представляется в виде 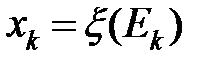 . Если все значения случайной величины совпадают между собой, то говорят, что случайная величина есть постоянная.
. Если все значения случайной величины совпадают между собой, то говорят, что случайная величина есть постоянная.
Случайную величину, принимающую конечное число значений, задают таблицей:
| Исходы | 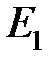 | 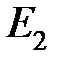 | …. | 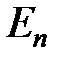 |
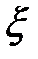 | 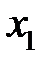 | 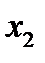 | 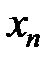 |
Примером случайной величины можно считать суммарное количество выпавших очков при одновременном бросании двух игральных кубиков. Очевидно, что число равновероятных исходов при опыте бросания двух кубиков равно 36. Значения, принимаемое случайной величиной, меняются от 2 до 12, причем, разным исходам могут соответствовать одинаковые значения. Например, значение 4 принимается при трех различных исходах: 1+3, 2+2 и 3+1.
Со случайными величинами обращаются так же, как с обычными числовыми функциями: можно складывать две случайные величины 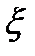 и
и 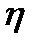 (то есть строить новую случайную величину, задавая таблицу с суммами соответствующих значений при всех исходах), умножать случайную величину на число, умножать и делить случайные величины друг на друга.
(то есть строить новую случайную величину, задавая таблицу с суммами соответствующих значений при всех исходах), умножать случайную величину на число, умножать и делить случайные величины друг на друга.
Для изучения случайной величины вводят ее числовые характеристики.
Математическим ожиданием случайной величины 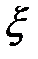 в опыте с
в опыте с 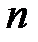 равновероятными исходами называется число
равновероятными исходами называется число 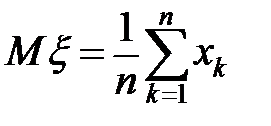 . То есть, математическое ожидание – это среднее значение случайной величины.
. То есть, математическое ожидание – это среднее значение случайной величины.
Очевидно следующие из определения свойства математического ожидания:
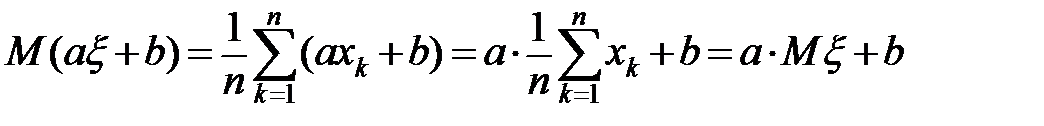 ,
,
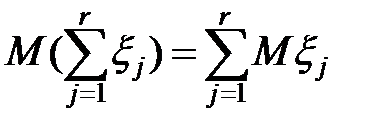 .
.
В данном выше определении математического ожидания очень существенно то, что исходы 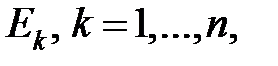 равновероятны. Представим теперь, что изучаемая нами случайная величина принимает в результате
равновероятны. Представим теперь, что изучаемая нами случайная величина принимает в результате 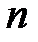 исходов
исходов  значений
значений 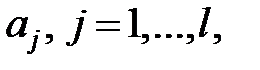 где
где  . Это означает, что какие-то из значений
. Это означает, что какие-то из значений 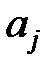 принимаются в результате нескольких равновероятных исходов. Объединим те исходы
принимаются в результате нескольких равновероятных исходов. Объединим те исходы 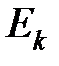 , которые соответствуют значению
, которые соответствуют значению 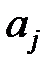 в событие
в событие 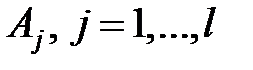 . Очевидно, что события
. Очевидно, что события 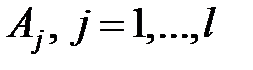 , попарно несовместны. Если обозначить через
, попарно несовместны. Если обозначить через 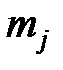 количество равновероятных исходов
количество равновероятных исходов 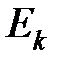 , соответствующих значению
, соответствующих значению 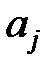 , то мы получим следующее определение математического ожидания:
, то мы получим следующее определение математического ожидания: 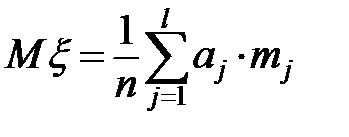 . А теперь заметим, что
. А теперь заметим, что 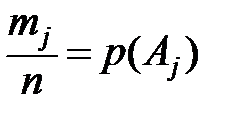 . Таким образом, мы получили новое определение математического ожидания: пусть полной группой исходов опыта являются события
. Таким образом, мы получили новое определение математического ожидания: пусть полной группой исходов опыта являются события 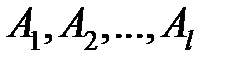 с вероятностями
с вероятностями 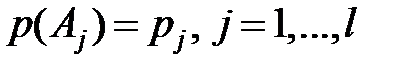 , причем случайная величина
, причем случайная величина 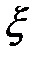 в результате исхода
в результате исхода 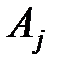 принимает значение
принимает значение 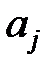 и все значения
и все значения 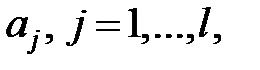 различны. Тогда
различны. Тогда 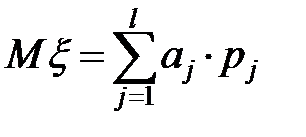 .
.
Таким образом, для вычисления математического ожидания случайной величины недостаточно знать только значения величины при различных исходах, необходимы также вероятности событий, обеспечивающих различные значения случайной величины. Поэтому целесообразно задавать таблицу, в которой указываются различные значения случайной величины, а также вероятности соответствующих исходов:
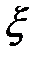 | 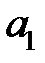 | 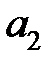 | … |  |
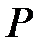 | 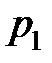 | 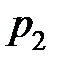 | … | 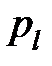 |
Построенная нами таблица называется законом (рядом) распределения дискретной случайной величины 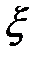 .Заметим, что сумма вероятностей, находящихся в нижней строке приведенной таблицы равна 1. Для наглядности закон распределения задают графически: на оси
.Заметим, что сумма вероятностей, находящихся в нижней строке приведенной таблицы равна 1. Для наглядности закон распределения задают графически: на оси 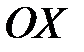 откладывают всевозможные значения случайной величины
откладывают всевозможные значения случайной величины 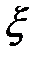 , а над каждым значением (вдоль оси
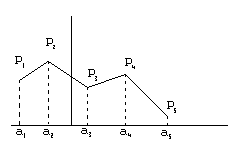
, а над каждым значением (вдоль оси 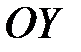 ) помещают соответствующую вероятность. Соединяя полученные точки отрезками, мы получим многоугольник (полигон) распределения.
) помещают соответствующую вероятность. Соединяя полученные точки отрезками, мы получим многоугольник (полигон) распределения.
Пример. Стрелок стреляет пять раз по мишени. Вероятность попадания в мишень при каждом выстреле 0,8. Найти закон распределения случайной величины «число попаданий стрелка в результате всех выстрелов».
Данная случайная величина принимает 6 значений: 0, 1, 2, 3, 4, 5. Подсчитаем вероятность каждого из исходов с применением формулы Бернулли. Значение 0 величина примет с вероятностью 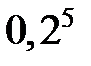 . Значение 1 – с вероятностью
. Значение 1 – с вероятностью 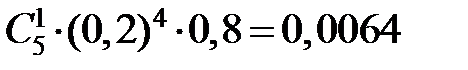 , значение 2 – с вероятностью
, значение 2 – с вероятностью 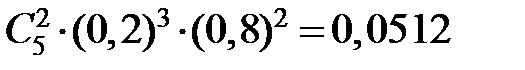 , значение 3 – с вероятностью
, значение 3 – с вероятностью 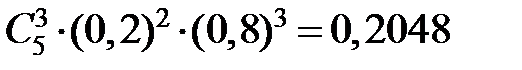 , значение 4 – с вероятностью
, значение 4 – с вероятностью 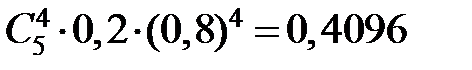 и значение 5 – с вероятностью
и значение 5 – с вероятностью 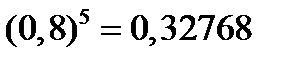 .
.
Построим закон распределения
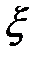 | ||||||
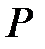 | 0,00032 | 0,0064 | 0,0512 | 0,2048 | 0,4096 | 0,32768 |
Задание. Постройте многоугольник распределения рассмотренной случайной величины.
Найдем математическое ожидание данной величины.
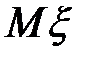 =
= 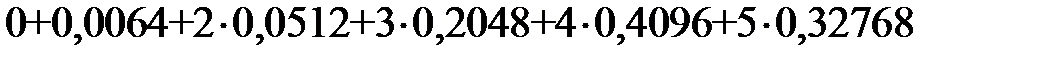 =4.
=4.
В соответствии с определением независимых событий две дискретные случайные величины 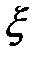 и
и 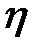 называются независимыми, если при любых
называются независимыми, если при любых 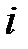 и
и  выполняется равенство
выполняется равенство 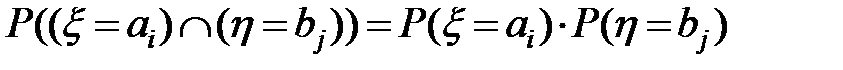 . Для независимых случайных величин характерно свойство
. Для независимых случайных величин характерно свойство 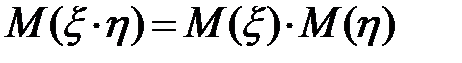 .
.
Если математическое ожидание дает нам значение, вокруг которого разбросаны значения случайной величины, то новая характеристика, называемая дисперсиейхарактеризуетстепень разброса значений случайной величины. Для вычисления дисперсии применяется формула 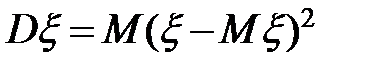 .
.
Найдем дисперсию случайной величины из предыдущего примера. Случайная величина 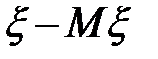 принимает значения -4, -3, -2, -1, 0, 1 с вероятностями 0,00032, 0,0064,
принимает значения -4, -3, -2, -1, 0, 1 с вероятностями 0,00032, 0,0064,
0,0512, 0,2048, 0,4096 и 0,32768, соответственно. Следовательно, величина 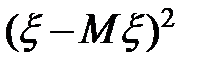 принимает значения 16, 9, 4, 1, 0 с вероятностями 0,00032, 0,0064, 0,0512, 0,53248 и 0,4096, соответственно. Поэтому
принимает значения 16, 9, 4, 1, 0 с вероятностями 0,00032, 0,0064, 0,0512, 0,53248 и 0,4096, соответственно. Поэтому 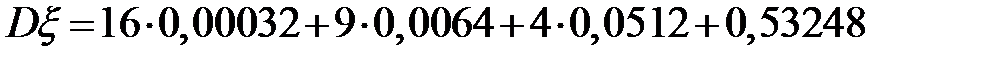 =0,8.
=0,8.
Для вычисления дисперсии иногда удобно пользоваться формулой 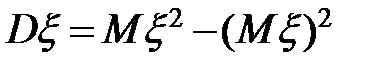 . Докажем, что эта формула следует из формулы, определяющей дисперсию. Используя
. Докажем, что эта формула следует из формулы, определяющей дисперсию. Используя
определение математического ожидания и то, что 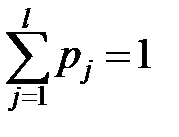 , получим
, получим
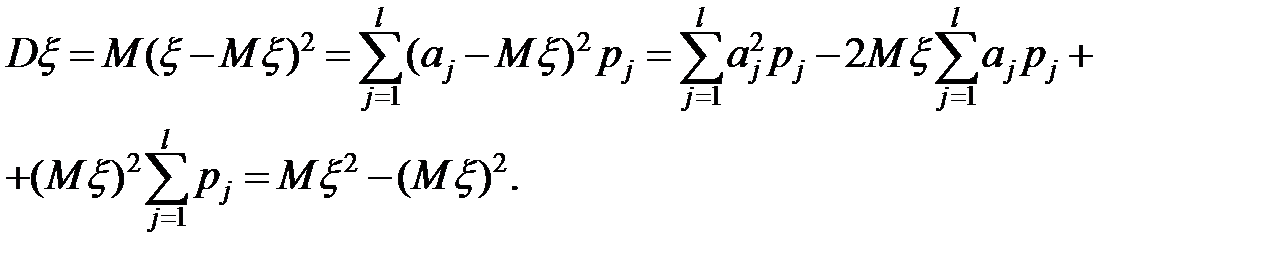
Нетрудно заметить, что 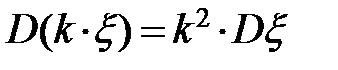 .
.
Часто при анализе каких-то процессов приходится выяснять, зависимы ли две случайные величины. Мы уже знаем, что в случае независимости 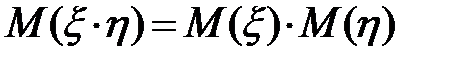 . Но если последнее равенство не выполняется, то можно оценить степень зависимости между случайных величин. Для этого служит коэффициент корреляции, вычисляемый по формуле
. Но если последнее равенство не выполняется, то можно оценить степень зависимости между случайных величин. Для этого служит коэффициент корреляции, вычисляемый по формуле 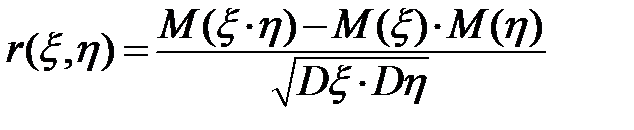 . Коэффициент корреляции обладает свойством
. Коэффициент корреляции обладает свойством 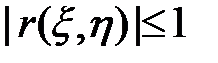 . Очевидно, что коэффициент корреляции двух независимых величин равен нулю. Если же две случайные величины связаны линейно, то есть,
. Очевидно, что коэффициент корреляции двух независимых величин равен нулю. Если же две случайные величины связаны линейно, то есть, 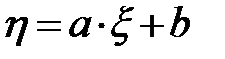 , то
, то 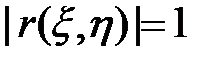 .
.
Справедливо следующее свойство независимых величин: если величины 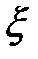 и
и 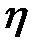 независимы, то
независимы, то 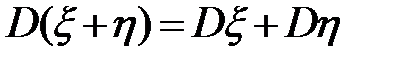 .
.
В случае, когда значение модуля коэффициента корреляции близко к 1, можно найти примерную линейную зависимость одной величины от другой, то есть, значения a и b методом наименьших квадратов. Соответствующая прямая называется прямой регрессии.
Задания.
1.Случайная величина Х задана рядом распределения:
| xi | -2 | |||
| рi | 0,08 | 0,4 | 0,32 | 0,2 |
1) Построить многоугольник распределения; 2) найти вероятности событий А = (Х<2); В = (1 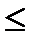 Х<3); С = (1<Х
Х<3); С = (1<Х 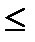 3); 3) найти М(Х); 4) найти D(Х).
3); 3) найти М(Х); 4) найти D(Х).
2. Случайная величина Y задана рядом распределения:
| уi | 1,1 | 1,4 | 1,7 | 2,0 | 2,3 |
| рi | 0,1 | 0,2 | С | 0,3 | 0,1 |
1) Найти значение Р(Y = 1,7); 2) построить многоугольник распределения; 3) найти вероятности Р(Y>1,4), P(1,4 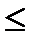 Y
Y 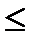 2,3); 4) найти М(Y); 5) найти D(Y).
2,3); 4) найти М(Y); 5) найти D(Y).
3.Закон распределения случайной величины X задан таблицей:
| xi | ||||
| рi | 0,1 | 0,4 | 0,3 | С |
Найти: 1) С, 2) М(Х), 3) D(Х), 4) Р(Х<3).
2. Непрерывная случайная величина.
В случае, когда значения случайной величины непрерывны, например, заполняют целиком интервал, невозможно задавать случайную величину в виде таблицы с конечным числом исходов. Примером непрерывной случайной величины является рост трехлетнего ребенка. Опыт состоит в измерении роста ребенка. Исход опыта – измерение роста конкретного ребенка. Очевидно, что нельзя установить конечное число возможных исходов, можно лишь указать диапазон значений роста по результатам многолетних наблюдений.
Для непрерывной случайной величины вводится функция распределения. По аналогии с законом распределения для дискретной величины функция распределения непрерывной случайной величины– это вероятность, но не вероятность того, что случайная величина принимает конкретное значение, а вероятность того, что случайная величина принимает значения, меньшие данного: 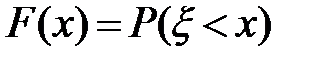 .
.
Если ввести такую же функцию распределения для дискретной величины, то эта функция окажется ступенчатой. Так, в последнем примере со стрелком 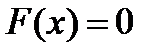 при
при 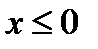 ,
, 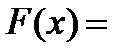 0,00032 при
0,00032 при 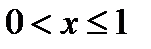 ,
, 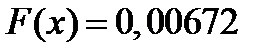 при
при 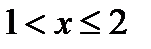 ,
, 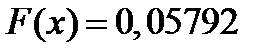 при
при 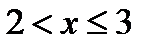 ,
, 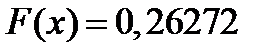 при
при 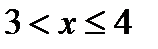 ,
, 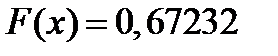 при
при 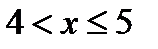 ,
, 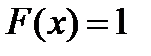 при
при 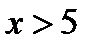 .
.
Поскольку функция распределения является вероятностью, ее значения расположены в диапазоне [0,1], при увеличении значений аргумента 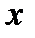 вероятность
вероятность 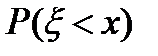 уменьшиться не может, так как множество возможных значений случайной величины
уменьшиться не может, так как множество возможных значений случайной величины 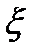 расширяется. Поэтому функция
расширяется. Поэтому функция 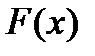 неубывающая,
неубывающая, 
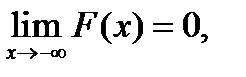
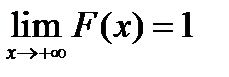 . Приведенный пример функции распределения дискретной величины подтверждает эти рассуждения.
. Приведенный пример функции распределения дискретной величины подтверждает эти рассуждения.
В случае непрерывной случайной величины график функции распределения – непрерывная кривая. Если функция 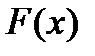 дифференцируема, то ее производная
дифференцируема, то ее производная 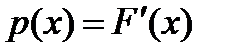 называется плотностью распределения.Вследствие неубывания функции распределения
называется плотностью распределения.Вследствие неубывания функции распределения 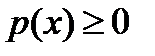 . Из формулы Ньютона-Лейбница следует, что
. Из формулы Ньютона-Лейбница следует, что 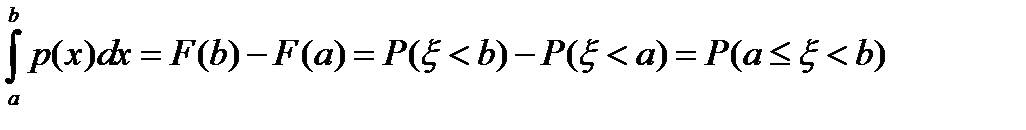 . Следовательно, в соответствии с геометрическим смыслом интеграла, вероятность того, что случайная величина принимает значения на полуинтервале
. Следовательно, в соответствии с геометрическим смыслом интеграла, вероятность того, что случайная величина принимает значения на полуинтервале 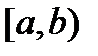 , равна площади криволинейной трапеции с основанием
, равна площади криволинейной трапеции с основанием 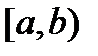 , ограниченной сверху кривой
, ограниченной сверху кривой 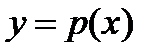 . Очевидно, что площадь криволинейной трапеции не изменится, если в ее основании полуинтервал
. Очевидно, что площадь криволинейной трапеции не изменится, если в ее основании полуинтервал 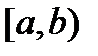 заменить на отрезок
заменить на отрезок 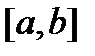 или на интервал
или на интервал 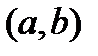 . То есть,
. То есть,
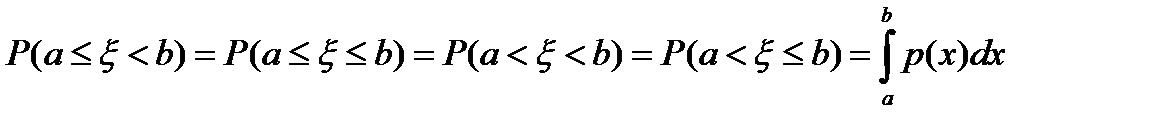 .
.
Заметим, что для непрерывной случайной величины, в отличие от дискретной случайной величины, вероятность того, что величина принимает какое-то конкретное значение, равна нулю. Действительно, 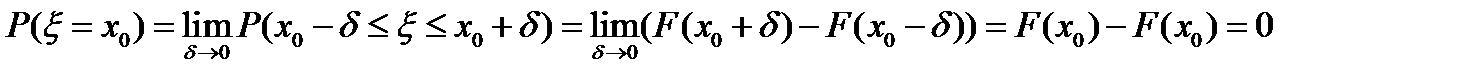 .
.
Очевидно, что 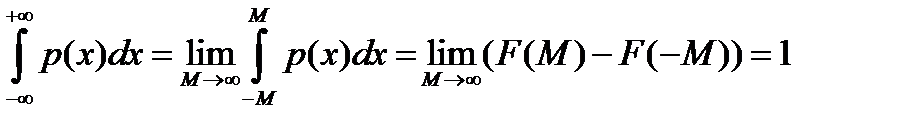 и
и 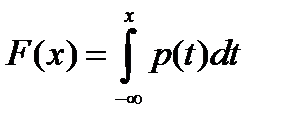 .
.
Математическое ожидание для непрерывной случайной величины 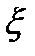 с дифференцируемой плотностью распределения определяется как
с дифференцируемой плотностью распределения определяется как 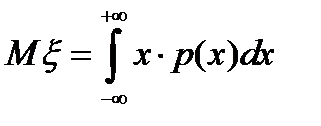 .
.
Дисперсия непрерывной случайной величины так же, как и для дискретной случайной величины определяется как 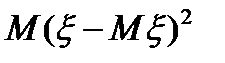 и также выражается с помощью интеграла в случае дифференцируемой функции распределения.
и также выражается с помощью интеграла в случае дифференцируемой функции распределения.
Две непрерывные случайные величины 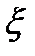 и
и 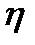 называются независимыми, если для любой пары промежутков
называются независимыми, если для любой пары промежутков 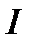 и
и 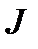 справедливо:
справедливо: 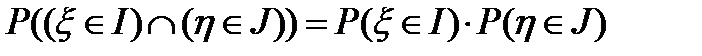 . Так же как в случае дискретных величин имеет место соотношение
. Так же как в случае дискретных величин имеет место соотношение 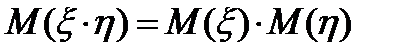 .
.
Задания.
1.Задана функция распределения непрерывной случайной величины Х
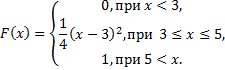
Найти: 1) Плотность распределения 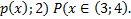
2.Задана плотность распределения непрерывной случайной величины Х
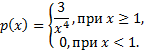
Найти 1) Функцию распределения F(x); 2) 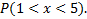
3. Задана функция
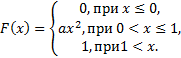
Определить:1) при каком значении 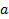 функция
функция 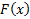 будет функцией распределения некоторой случайной величины Х; 2) плотность вероятности ; 3) вероятность события D=
будет функцией распределения некоторой случайной величины Х; 2) плотность вероятности ; 3) вероятность события D= 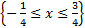 .
.
4.Данаплотность распределения вероятностей случайной величины Х:
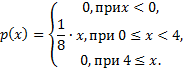
Найти 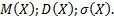
5.Найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины Х с плотностью вероятности