Определение качественных показателей зацепления
Качественными показателями зацепления являются коэффициенты перекрытия 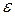 , относительного скольжения λ и удельного давления γ.
, относительного скольжения λ и удельного давления γ.
Коэффициент торцевого перекрытия 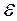 - это отношение угла торцевого перекрытия зубчатого колеса цилиндрической передачи к его угловому шагу.
- это отношение угла торцевого перекрытия зубчатого колеса цилиндрической передачи к его угловому шагу.
Также коэффициентом перекрытия 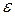 называют отношение длины k дуги зацепления к длине шага pw по начальным окружностям колес:
называют отношение длины k дуги зацепления к длине шага pw по начальным окружностям колес:
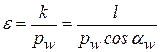 .
.
Формула неудобна для подсчетов, так как в нее входит шаг pw, который не задан. Так как 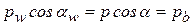 ,
,
где pb— шаг зацепления на основных окружностях, то
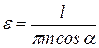 .
.
Используя полученную формулу, определяют коэффициент перекрытия по чертежу. Для этого нужно измерить длину активной части линии зацепления l непосредственно на чертеже и значение ее подставить в формулу.
Коэффициент перекрытия характеризует плавность зацепления и показывает среднее число пар зубьев, находящихся одновременно в зацеплении. Чем больше коэффициент перекрытия, тем более плавно и бесшумно работает передача.
Коэффициентом перекрытия 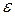 не должен быть меньше единицы, так как это приводит к перерывам в передаче движения от ведущего к ведомому и к ударам зубьев колес. Предельное значение коэффициента перекрытия в зубчатой передаче с нормальной высотой зуба равен 1,982. Если коэффициент перекрытия равен, например, 1,6, то это значит, что в среднем в зацеплении находится 1,6 пары зубьев, т.е. фактически 60% времени в зацеплении находятся две пары зубьев, а 40% - одна пара зубьев.
не должен быть меньше единицы, так как это приводит к перерывам в передаче движения от ведущего к ведомому и к ударам зубьев колес. Предельное значение коэффициента перекрытия в зубчатой передаче с нормальной высотой зуба равен 1,982. Если коэффициент перекрытия равен, например, 1,6, то это значит, что в среднем в зацеплении находится 1,6 пары зубьев, т.е. фактически 60% времени в зацеплении находятся две пары зубьев, а 40% - одна пара зубьев.
При проектировании зубчатого зацепления рекомендуется принимать допустимое значение коэффициента перекрытия 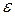 = 1,2.
= 1,2.
Коэффициенты относительного скольжения. Так как рабочие участки профилей зубьев перекатываются друг по другу со скольжением, то на этих участках возникают силы трения и происходит процесс изнашивания. Характеристикой вредного влияния скольжения являются коэффициенты λ1 и λ 2 относительного скольжения, которые определяют по формулам
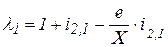 ;
;
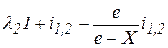 ,
, 
где е = N1N2 — длина теоретической линии зацепления, а
i1,2= 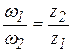 ;
;
i2,1= 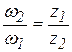 ;
;
Х — расстояние от точки N1 касания теоретической линии зацепления с основной окружностью первого (меньшего) колеса, отсчитываемое в направление к точке N2.
Составим таблицу 2 значений λ 1и λ 2. Для этого измеряем длину е на рис. 8, подсчитываем ряд значений λ 1и λ 2, изменяя Х в границах от 0 до е с интервалами 15-30 мм.
Необходимо знать, что в полюсе зацепления Р коэффициенты λ 1и λ 2 равны нулю.
Значения коэффициентов λ 1и λ 2
Таблица 2
| Х | ..... | N1 | ..... | е | |
| λ 1 | - ∞ | ..... | ..... | ||
| λ 2 | ..... | ..... | - ∞ |
Пользуясь данными, приведенными в табл. 2, строим диаграммы для значений коэффициентов λ 1 и λ 2 в прямоугольной системе координат (рис. 8). Через какую-либо точку О линии 01N1 проводим ось абсцисс Ох, параллельную прямой N1N2. Тогда линия 0N1 будет осью ординат. Пользуясь табл. 2, строим диаграммы для λ 1и λ 2 (кривые RP1S и QP1U)
Необходимо отметить, что таблица значений λ1и λ2 составлена в предположении, что окружности головок колес проходят через точки N1 и N2, то есть зацепление зубьев происходит по всей теоретической линии зацепления от точки N1 до точки N2 и что рабочие участки профилей зубьев кончаются у соответствующих основных окружностей. Поэтому построенные диаграммы для λ 1 и λ 2 дают значения коэффициентов удельного скольжения также для тех участков профилей на ножках зубьев (участки A1С и В2Е), которые не участвуют в зацеплении, а также и для тех участков профилей на головках, которые в действительности отсутствуют.
Для того чтобы выделить те части диаграмм, которые дают значения λ1 и λ2 для фактически имеющихся на зубьях рабочих участков профилей, нужно через точки а и b провести перпендикуляры к линии зацепления, которые отсекут на диаграммах интересующие нас участки (заштрихованы на рис. 8).
Далее строим круговые диаграммы, откладывая от соответствующих точек рабочих участков профилей зубьев на концентрических окружностях дуги, равные (или пропорциональные) ординатам прямоугольных диаграмм.
На рис. 8 приведены круговые диаграммы А''1В''1 и А''2В''2.
Для уяснения техники построения круговых диаграмм покажем построение ординаты D'1D''1 круговой диаграммы А''1В''1 которая соответствует ординате у1 прямоугольной диаграммы RS. Продолжая ординату y1 находим точку d,являющуюся точкой зацепления, в которой λ1 имеет значение, определяемое ординатой у1.Засекая профиль А'1В'1, в точке D'1 дугой dD'1 радиуса O1d находим точку D'1 профиля зуба, для которой λ1 имеет значение, определяемое ординатой y1.На дуге dD'1 отложим от точки D'1 дугу D'1D''1, равную (или пропорциональную) ординате y1.
Аналогичным построением находим дугу D'2D''2, которая является ординатой круговой диаграммы А''2В''2, соответствующей ординате у2 диаграммы QU.
Коэффициент удельного давления учитывает влияние геометрии зубьев (радиус кривизны их профилей) на величину контактных напряжений, возникающих в местах соприкосновения зубьев.
Коэффициентом удельного давления 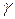 называется отношение модуля зацепления к приведенному радиусу кривизны эвольвентных профилей:
называется отношение модуля зацепления к приведенному радиусу кривизны эвольвентных профилей: 
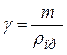 .
.
На рис. 9 представлена диаграмма изменения коэффициента γ в зависимости от радиуса кривизны 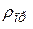 . Коэффициенту имеет минимальное значение в середине теоретической линии зацепления N1N2 .
. Коэффициенту имеет минимальное значение в середине теоретической линии зацепления N1N2 .
При расчете зубьев на контактную прочность коэффициент 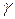 определяется по формуле:
определяется по формуле:
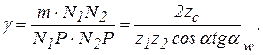
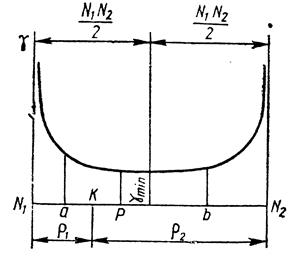
Рис. 9
