Линейная зависимость и независимость

Функции называются линейно независимыми, если

(допустима только тривиальная линейная комбинация функций, тождественно равная нулю). В отличие от линейной независимости векторов здесь тождество линейной комбинации нулю, а не равенство. Это и понятно, так как равенство линейной комбинации нулю должно быть выполнено при любом значении аргумента.

Функции называются линейно зависимыми, если существует не нулевой набор констант (не все константы равны нулю) 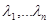, такой что 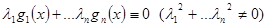(существует нетривиальная линейная комбинация функций, тождественно равная нулю).

Теорема. Для того чтобы функции были линейно зависимы, необходимо и достаточно, чтобы какая-либо из них линейно выражалась через остальные (представлялась в виде их линейной комбинации).

Докажите эту теорему самостоятельно, она доказывается так же, как аналогичная ей теорема о линейной зависимости векторов.

Определитель Вронского.

Определитель Вронского для функций вводится как определитель, столбцами которого являются производные этих функций от нулевого (сами функции) до n-1 го порядка.

.

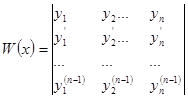Теорема. Если функции 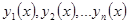линейно зависимы, то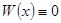

Доказательство. Так как функции 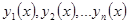линейно зависимы, то какая-либо из них линейно выражается через остальные, например,

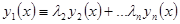. Тождество можно дифференцировать, поэтому

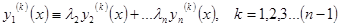. Тогда первый столбец определителя Вронского линейно выражается через остальные столбцы, поэтому определитель Вронского тождественно равен нулю.

Теорема.Для того, чтобы решения линейного однородного дифференциального уравнения n-ого порядка были линейно зависимы, необходимо и достаточно, чтобы .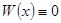

Доказательство. Необходимость следует из предыдущей теоремы.

Достаточность. Зафиксируем некоторую точку 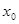. Так как 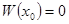, то столбцы определителя, вычисленные в этой точке, представляют собой линейно зависимые векторы.

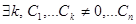, что выполнены соотношения

.

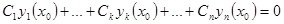
Так как линейная комбинация решений линейного однородного уравнения является его решением, то можно ввести решение вида

- линейную комбинацию решений с теми же коэффициентами.

Заметим, что при 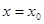это решение удовлетворяет нулевым начальным условиям, это следует из выписанной выше системы уравнений. Но тривиальное решение линейного однородного уравнения тоже удовлетворяет тем же нулевым начальным условиям. Поэтому из теоремы Коши следует, что введенное решение тождественно равно тривиальному, следовательно,

,

поэтому решения линейно зависимы.

Следствие. Если определитель Вронского, построенный на решениях линейного однородного уравнения, обращается в нуль хотя бы в одной точке, то он тождественно равен нулю.

Доказательство. Если 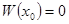, то решения линейно зависимы, следовательно, .

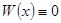Теорема.1. Для линейной зависимости решений необходимо и достаточно 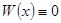(или ).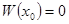

2. Для линейной независимости решений необходимо и достаточно .

Доказательство. Первое утверждение следует из доказанной выше теоремы и следствия. Второе утверждение легко доказывается от противного.

Пусть решения линейно независимы. Если 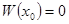, то решения линейно зависимы. Противоречие. Следовательно, .

Пусть . Если решения линейно зависимы, то 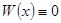, следовательно, 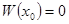, противоречие. Поэтому решения линейно независимы.

Следствие.Обращение определителя Вронского в нуль хотя бы в одной точке является критерием линейной зависимости решений линейного однородного уравнения.

Отличие определителя Вронского от нуля является критерием линейной независимости решений линейного однородного уравнения.

Теорема.Размерность пространства решений линейного однородного уравнения n-ого порядка равна n.

Доказательство.

a) Покажем, что существуют n линейно независимых решений линейного однородного дифференциального уравнения n-го порядка. Рассмотрим решения 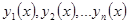, удовлетворяющие следующим начальным условиям:

...........................................................

Такие решения существуют. В самом деле, по теореме Коши через точку проходит единственная интегральная кривая – решение. Через точку 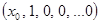проходит решение 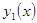, через точку

- решение , через точку 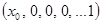- решение .

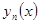Эти решения линейно независимы, так как .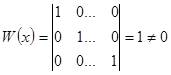

b) Покажем, что любое решение линейного однородного уравнения линейно выражается через эти решения (является их линейной комбинацией).

Рассмотрим два решения. Одно - произвольное решение 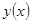с начальными условиями . Справедливо соотношение

..........................................................................

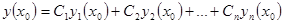
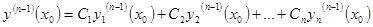, где

.

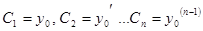Второе решение – это линейная комбинация решений с теми же коэффициентами .

Вычисляя начальные условия в точке 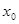для решения 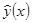, убеждаемся, что они совпадают с начальными условиями для решения 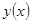. Следовательно, по теореме Коши, произвольное решение 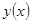представляется в виде линейной комбинации линейно независимых решений .

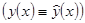Таким, образом, существует n линейно независимых решений линейного однородного дифференциального уравнения n-ого порядка, и произвольное решение линейно выражается через эти решения . Поэтому размерность пространства решений линейного однородного дифференциального уравнения n-ого порядка равна n. .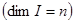

Любые n линейно независимых решений линейного однородного дифференциального уравнения n-ого порядка представляют собой базис пространства решений или фундаментальную систему решений.