Нахождение углового коэффициента касательной.

Если имеется кривая заданная функцией y=f(x), то угловой коэффициент касательной в точке с абсциссой x₀ находят по формуле

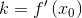
Например 1. Найти угловой коэффициент касательной, проведенной к графику функции

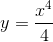в точке с абсциссой х₀=1.
Решение. Находим производную функции

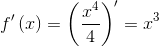
Тогда при x₀=1 значение производной равно

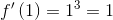
Отсюда получаем, что угловой коэффициент касательной в точке с абсциссой х₀=1 равен

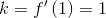
Нахождение угла наклона касательной к графику функции.

Геометрический смысл производной заключается в том, что производная равна угловому коэффициенту касательной и тангенсу угла наклона.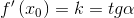

Как найти угол наклона касательной к графику функции y=f(x) в точке x_0.

Например. Найти наклона касательной, проведенной к графику функции

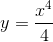в точке с абсциссой х₀=1.
Решение. Находим производную функции

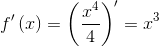
Тогда при x₀=1 значение производной равно 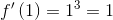,где

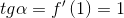. Отсюда находим угол .

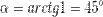Исследование функции с помощью производной.

Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.

Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

Промежутки возрастания и убывания функции называются интервалами монотонностиданной функции.

Экстремумы функции.

Точка X0 называется точкой максимума функции f (x), если существует такая окрестность точки X0, что для всех X из этой окрестности выполняется неравенство f (x) < f (x0).

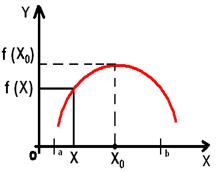
Точка X0 называется точкой минимума, если существует такая окрестность точки X0, что для всех X из этой окрестности выполняется неравенство f (x) > f (x0).

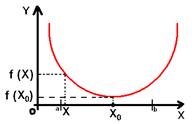
Теорема Ферма.
(Необходимое условие экстремума)
Если X0 – точка экстремума функции f (x), то f’ (x0)=0

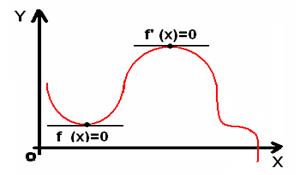
Точки в которых f’ (x)=0 называются стационарными или критическими.

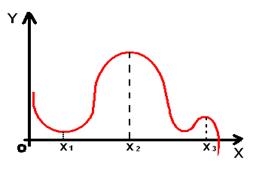
Точки, в которых производная функции равна нулю на графике функции выглядят так:

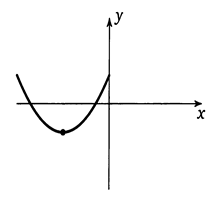
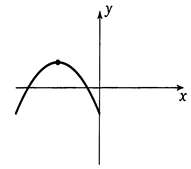
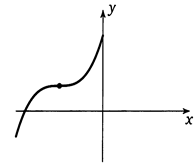
Достаточное условие существования экстремума (максимума) в точке.

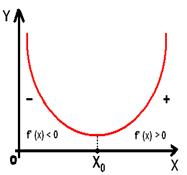
Если при переходе через стационарную точку производная функции меняет знак с “+” на “-”, то эта точка является точкой максимума.

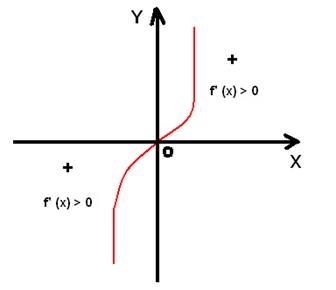
Если при переходе через стационарную точку f’ (x) не меняет знак, то эта точка не является точкой экстремума, такие точки называются точками перегиба.

Алгоритм нахождения экстремумов функции.

1. Найти производную функции.

2. Найти стационарные точки (решить уравнение f’ (x)=0).

3.На числовой прямой определить знак производной на полученных интервалах.

4.Определить точки экстремумов функции (использовать определение).

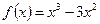5. Записать ответ.

Например: Найти экстремумы функции

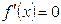
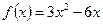1.

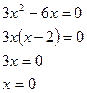2.

3.___+____.___-____.___+_______

0 2

4.Х=0 – точка максимума, т. К. при переходе через стационарную точку производная сменила знак с «+» на «-»;

Х=2 – точка минимума, т. К. при переходе через стационарную точку производная сменила знак с «-» на «+»;

5. ответ: х=0 – точка максимума, х=2 – точка минимума.