Бесконечные и односторонние производные

I Бесконечные производные

Определение 1. Говорят, что функция 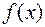имеет в точке x₀ бесконечную производную, если

.

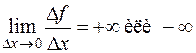При этом пишут 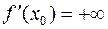или .

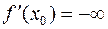Пример 1. , :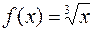

.

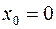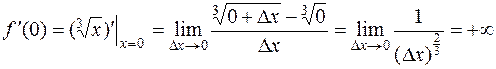II Односторонние производные

Определение 2. Правая 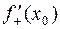и левая 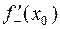производные функции 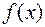в точке x₀, определяются равенствам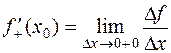и:

и .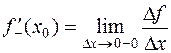

Из общих теорем о пределах можно получить такую теорему.

Теорема 1. Функция 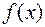имеет в точке x₀ производную тогда и только тогда, когда она имеет в этой точке равные друг другу односторонние производные.

Пример 2. Для функции 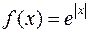найти правую и левую производную в нуле.

,

.

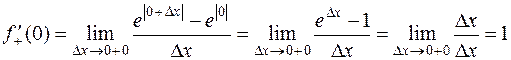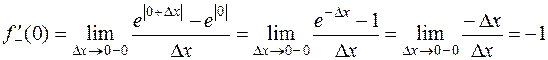Так как 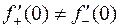, то 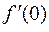не существует.

Следующая теорема позволяет в некоторых случаях упростить вычисление односторонних производных.

Теорема 2. Пусть функция 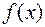имеет в интервале 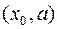конечную производную 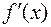, причем, существует (конечный или нет) 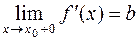. Тогда в точке x₀ существует правая производная и .

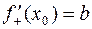Аналогичное утверждение имеет место и для левой производной.

В §2 была вычислена производная функции 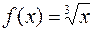для 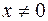: 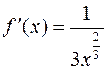. Результат примера 1 ( 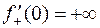) с помощью теоремы 2 получается моментально:

.

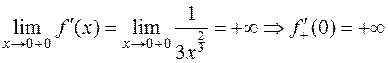Аналогично получается и 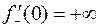. Совпадение односторонних производных означает, что и .

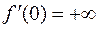Замечание. Если у функции 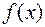существуют конечные, не равные друг другу производные 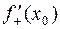и 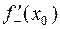, то у графика функции имеются не совпадающие правая и левая касательные в точке 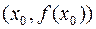. Такая точка графика называется угловой. Если же производная (хотя бы односторонняя) равна +¥ или 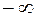, то это означает, что у графика имеется вертикальная касательная.