Дана автокорреляционная функция временного ряда

Верным будет утверждение, что ряд …

имеет выраженную сезонную компоненту с лагом 4

содержит только тенденцию, и не содержит сезонной компоненты

имеет выраженную сезонную компоненту с лагом 6

не имеет ни тенденции, ни сезонной компоненты, имеет только случайную компоненту

Решение:

Высокое значение коэффициентов автокорреляции четвертого и кратного ему восьмого уровней позволяет сделать вывод, что ряд имеет выраженную сезонную компоненты, периодичность которой равна четырем.
Низкое значение коэффициента автокорреляции первого порядка позволяет предположить, что ряд не содержит трендовой компоненты.

3. Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции …

первого, второго, третьего и последующих порядков

между трендовой, сезонной и случайной компонентами

между несколькими временными рядами

факторов, формирующих уровень ряда

Решение:

Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции первого, второго и последующих порядков.

4. Значение коэффициента автокорреляции второго порядка равно (-0,6), следовательно, ряд содержит …

тенденцию

убывающую тенденцию

затухающую сезонную волну периодичностью 2 момента времени

полиномиальную тенденцию с точкой минимума

Решение:

Структура временного ряда определяется по значениям коэффициента автокорреляции, рассчитанным для разных порядков. Коэффициент автокорреляции характеризует тесноту связи между уровнями исходного ряда и уровнями этого же ряда, сдвинутыми на значение порядка коэффициента автокорреляции. Если временной ряд содержит тенденцию, то наиболее высокое (максимальное или чуть меньше, чем максимальное) значение наблюдается у коэффициента автокорреляции первого и/или второго порядка. Однако, по знаку коэффициента автокорреляции нельзя делать вывод о направленности тенденции. Поэтому вариант «ряд содержит убывающую тенденцию» является ошибочным, так как ряд при данном значении коэффициента автокорреляции может содержать и положительную тенденцию. Правильный вариант – «ряд содержит тенденцию».

5. Автокорреляцией уровней ряда называется корреляционная зависимость между …

последовательными уровнями ряда

уровнями двух рядов

компонентами, образующими уровни ряда

факторами, формирующими уровень ряда

Решение:

Автокорреляцией уровней ряда называется корреляционная зависимость между последовательными уровнями ряда.

Тема 19: Аддитивная и мультипликативная модели временных рядов

1. Уровень временного ряда (y_t) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для аддитивной модели временного ряда для уровня y₃ получено уравнение тренда T = 3,14 + 2,07t. Известны значения компонент: S₃ = 1,6; E₃ = –0,3. Тогда значение уровня временного ряда y₃ будет равно …

10,65

9,35

1,3

6,51

Решение:

Аддитивная модель временного ряда записывается в виде выражения 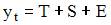и предполагает, что сумма компонент ряда T, S и Е равна значению уровня ряда y_t. Расчет компоненты Т осуществим по формуле T = 3,14 + 2,07t , где t = 3, так как необходимо рассчитать значение уровня y₃.
Получаем: y₃ = 3,14 + 2,07 * 3 +1,6 + (–0,3) = 10,65.

2. Уровень временного ряда (y_t) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для мультипликативной модели временного ряда, содержащего периодические колебания в 4 момента, получены значения сезонных компонент: S₁ = 2,087; S₂ = 0,632; S₃ = 0,931; S₄ = 3,256. Известны значения компонент: T₅ = 20,6 и E₅ = 0,4. Рассчитайте значение уровня временного ряда y₅.

17,2

23,1

0,83

Решение:

Аддитивная модель временного ряда записывается в виде выражения 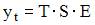и предполагает, что произведение компонент ряда T, S и Е равно значению уровня ряда y_t. Значение компоненты S определим из имеющихся, так как необходимо рассчитать значение уровня y₅, периодичность колебаний составляет 4 момента времени, тогда для t = 5 значение компоненты S₅ = S₁ = 2,087. Получаем: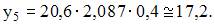

3. Для аддитивной модели временного ряда Y = T + S + E лаг модели равен 4 и известны значения трех скорректированных сезонных компонент: 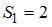, , 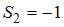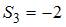. 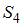равна …

Решение:

Для аддитивной модели временного ряда Y = T + S + E сумма скорректированных сезонных компонент равна нулю. .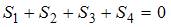
Значит,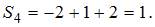

4. Для мультипликативной модели временного ряда Y = T · S · E сумма скорректированных сезонных компонент равна …

лагу

половине лага

Решение:

Для мультипликативной модели временного ряда Y = T · S · E сумма скорректированных сезонных компонент равна лагу.

Тема 20: Модели стационарных и нестационарных временных рядов и их идентификация

1. Известно, что дисперсия временного ряда Y увеличивается с течением времени. Значит, ряд Y …

нестационарным

стационарным

автокорреляционным

сбалансированным

Решение:

Временной ряд называется стационарным, если он является конкретной реализацией стационарного стохастического процесса. Под стационарным в слабом смысле понимается стохастический процесс, для которого среднее и дисперсия независимо от рассматриваемого периода времени имеют постоянное значение. Автоковариация зависит только от длины лага между рассматриваемыми переменными. Если дисперсия ряда увеличивается, то есть она не постоянна, то ряд будет нестационарным.
Правильный ответ: временной ряд Y – нестационарный.

2. Известно, что временной ряд Y порожден случайным процессом, который по своим характеристикам является «белым шумом». Значит, ряд Y …

стационарный

нестационарный

автокорреляционный

сбалансированный

Решение:

По своим характеристикам временной ряд, образованный случайным процессом «белый шум», является стационарным. Математическое ожидание временного ряда, образованного случайным процессом «белый шум» постоянно, дисперсия постоянна, автоковариация зависит только от длины лага. Правильный ответ: временной ряд Y – стационарный.

3. Известно, что временной ряд Y характеризуется устойчивой тенденцией, то есть его среднее значение меняется. Значит, ряд Y, скорее всего,является …

нестационарным

стационарным

автокорреляционным

сбалансированным

Решение:

Временной ряд называется стационарным, если он является конкретной реализацией стационарного стохастического процесса. Под стационарным в слабом смысле понимается стохастический процесс, для которого среднее и дисперсия независимо от рассматриваемого периода времени имеют постоянное значение. Автоковариация зависит только от длины лага между рассматриваемыми переменными. Если среднее значения ряда меняется, то ряд будет нестационарным. Правильный ответ: временной ряд Y – нестационарный.

4. Для временного ряда известны характеристики: 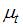– среднее и 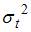– дисперсия. Если временной ряд является стационарным, то …

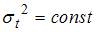
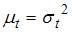
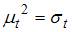
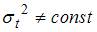
Решение:

При моделировании временных рядов рассматривается отдельный класс – стационарные временные ряды. Основные характеристики стационарного временного ряда состоят в том, что среднее 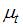и дисперсия стохастического процесса, сгенерировавшего конкретный временной, не зависят от времени t, то есть ; .

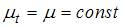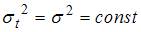Тема 21: Общие понятия о системах уравнений, используемых в эконометрике

Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных.

зависимых

эндогенных

экзогенных

независимых

Решение:

Система эконометрических уравнений включает множество переменных, среди которых выделяют экзогенные и эндогенные переменные. В левой части системы эконометрических уравнений находятся только эндогенные (зависимые) переменные.

2. Модель равенства спроса и предложения, где предложение 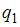и спрос 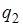являются линейными функциями цены p, состоит из уравнений …

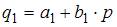
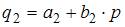
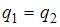
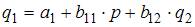
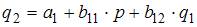
Решение:

В модели предложение 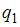и спрос 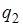являются линейными функциями цены p. Значит, уравнение для предложения 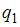будет иметь вид 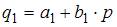, а уравнение для спроса – 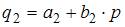. Так как рассматривается модель равенства спроса и предложения, значит, первые два уравнения должны быть дополнены третьим: .

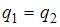Модель будет иметь вид

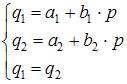
Системой эконометрических уравнений не является система линейных _____ уравнений.

нормальных

стандартизованных

рекурсивных

одновременных

Решение:

Система линейных одновременных уравнений является одним из видов систем эконометрических уравнений.

Система рекурсивных уравнений также является видом системы эконометрических уравнений.

Система нормальных уравнений используется при расчете оценок параметров линейных моделей с помощью МНК и не является системой эконометрических уравнений (правильный вариант ответа).

Стандартизованное уравнение регрессии используется при моделировании линейных уравнений множественной регрессии для расчета стандартизованных коэффициентов регрессии и ранжировании факторов по силе связи с зависимой переменной и не является системой эконометрических уравнений (правильный вариант ответа).

Тема 22: Классификация систем уравнений

1. При построении систем эконометрических уравнений различают три класса моделей:

(1) система независимых уравнений;

(2) система рекурсивных уравнений;

(3) система одновременных уравнений.

Отнесите предложенные модели к соответствующему классу.

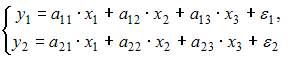
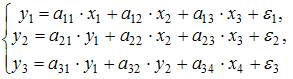
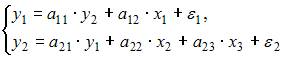
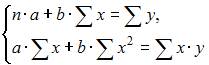
Решение:

Модель, в которой 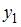– продуктивность коров, можно назвать моделью экономической эффективности сельскохозяйственного производства. Эта модель содержит в правой части только независимые переменные, поэтому она может быть отнесена к классу «система независимых уравнений».

Модель, в которой 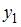– производительность труда, может быть названа моделью производительности труда и фондоотдачи. Это модель содержит в первом уравнении только независимые переменные, а во втором уравнении в правой части встречается и зависимая переменная 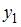; это значит, что модель можно отнести к классу «система рекурсивных уравнений».

Модель, в которой 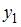– темп изменения месячной заработной платы, может служить моделью динамики цены и заработной платы. В правых частях обоих уравнений содержатся зависимые переменные, поэтому данная модель может быть отнесена к классу «система одновременных уравнений».
Система, в которой y – объем производства, вообще не является какой бы то ни было системой эконометрических уравнений – это система нормальных уравнений для определения параметров парной линейной регрессии.