Расчет, на прочность при изгибе

Рассчитать на прочность — это значит определить напряжение и сравнить его с допустимым.

Условие прочности при изгибе:

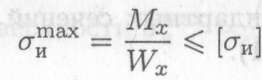
где [σ_иJ — допускаемое напряжение.

По этому неравенству проводят проверочные расчеты после окончания конструирования балки.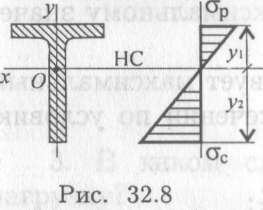

Для балок из хрупких материалов расчеты ведут по растянутой и сжатой зоне одновременно (рис. 32.8).

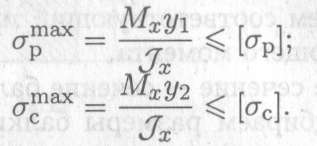
При проектировочном расчете определя­ют потребные размеры поперечных сечений балки или подбирают материал.

Схема нагружения и действующие нагрузки известны.

По условию прочности можно определить нагрузочную способ­ность балки[М_и] = W_x [сг].

Расчет на прочность при изгибе

Распределение нормальных и касательных напряжений при изгибе

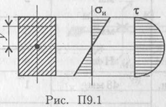
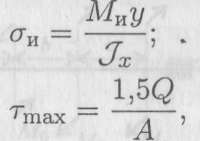
где М_и — изгибающий момент в сечении; Q — поперечная сила в сечении; у — расстояние до нейтрального слоя; J_x — осевой момент инерции сечения (рис. П9.1);

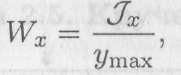
Wx — осевой момент сопротивления сечения; А — площадь сечения.

Условие прочности при изгибе

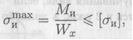
где [σ_и] — допускаемое напряжение.

Знаки изгибающих моментов и поперечных сил (рис. П9.2)

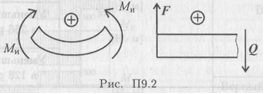
Задание:

1. Построить эпюры поперечных сил и изгибающих моментов.

2. Определить прогиб балки, нагруженной распределенной нагрузкой q = 100 H∙м и силой P = 40 Н, m = 200Н∙ м и произвести расчет на жесткость, если

[σ] =100 Н/мм²,

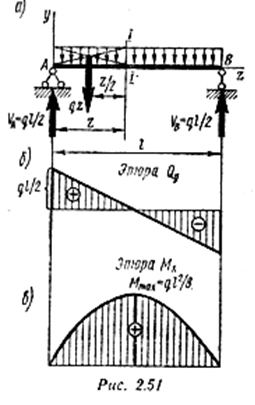
Пример 1:Определить прогиб посередине пролета балки, нагруженной равномерно распределенной нагруз­кой (см. рис. 2.51, а).

Решение

Поместим начало координат на левой опоре балки и составим обобщенные уравнения упругой линии и углов поворота:

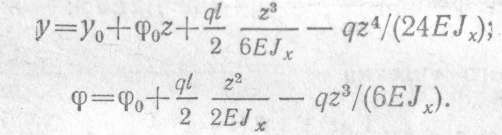
Определяем начальные параметры y₀ и φ₀ исходя из условия опорных закреплений:

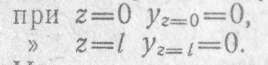
Из первого условия находим у₀ = 0.

Из второго условия определяем φ₀:

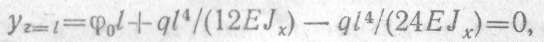
Откуда

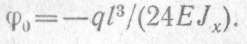
Подставляя у₀ и φ₀в уравнение прогибов, получаем

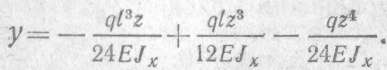
В середине пролета при z = 0,5l прогиб принимает максимальное значение

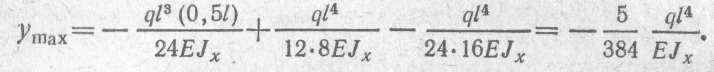
Знак минус перед значением прогиба показывает, что он направлен вниз, т. е, в сторону, противоположную по­ложительному направлению оси у.

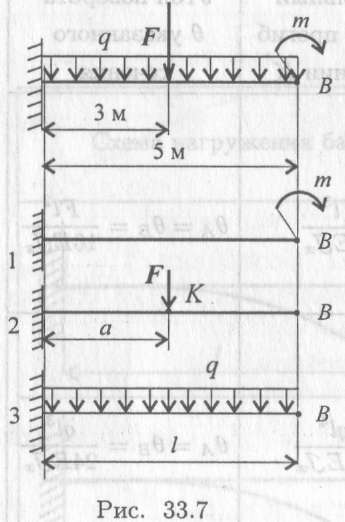
Пример 2:Проверить жесткость двутавровой балки (рис. 33.7). Принять

Сечение балки — двутавр № 45.

Решение

Используем принцип независимости действия сил. По приведен­ным в таблице формулам рассчитываем прогиб балки в точке от каждого вида нагружения отдельно (рис. 33.7 (1, 2, 3)).

Поскольку все действующие нагрузки прогибают балку вниз, результаты дей­ствия нагрузок можно сложить. Получен­ный суммарный прогиб сравним с допус­каемым прогибом.

Допускаемый прогиб

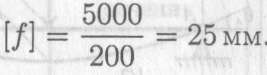
Суммарный прогиб

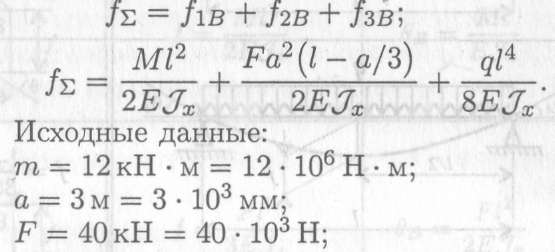
q = 4кН/ м = 4Н/мм; l = 5м = 5-10³мм.

Для двутавра № 45 ГОСТ 8239-89

J_x = 27696 см⁴ = 27,7 • 10⁷мм⁴.

Тогда

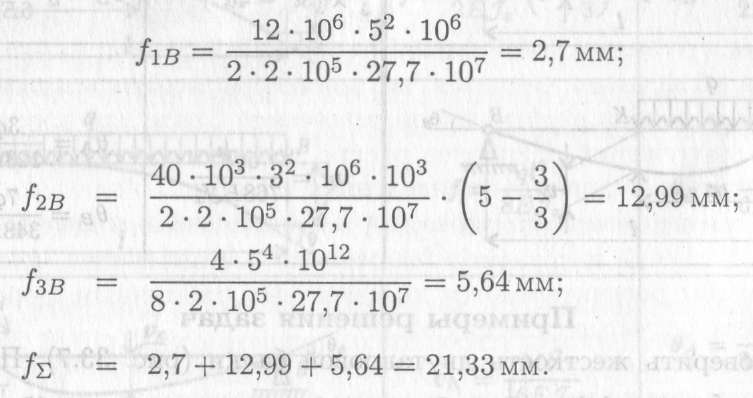
21,33 < 25 — условие жесткости выполняется. Максимальный прогиб не превышает допускаемого значения.

1	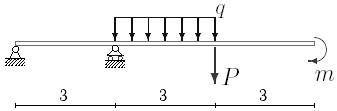2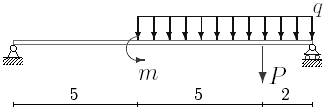
3	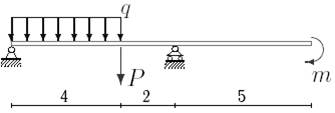4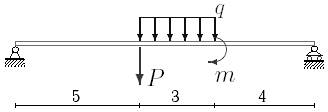
5	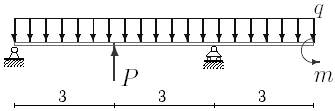6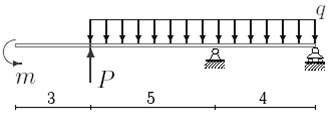
7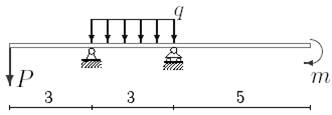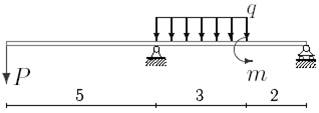
9	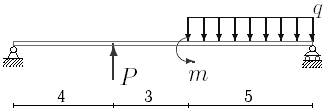10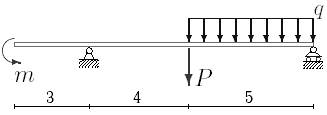
11	12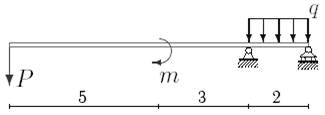
13	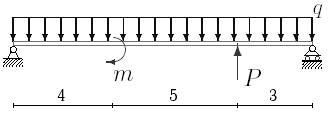14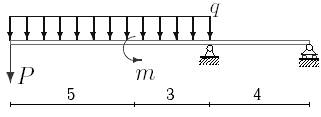
15	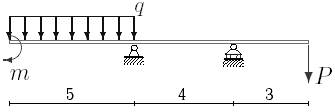16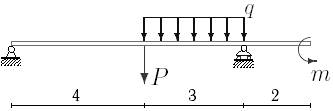
17	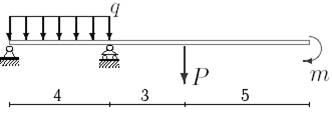18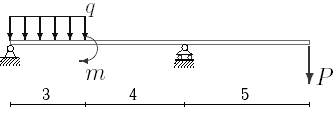
19	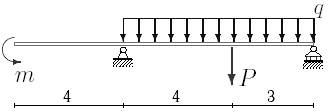20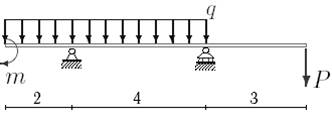
21	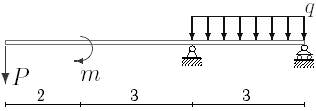22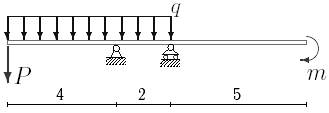
23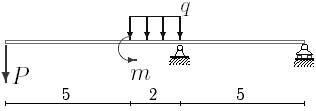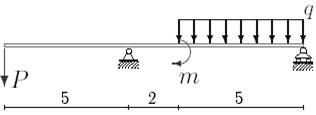
25	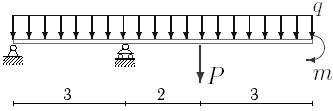26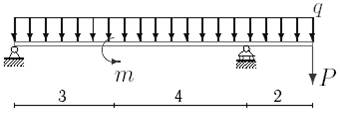

Контрольные вопросы:

1. Какие внутренние силовые факторы возникают в сечении бал­ки при чистом и поперечном изгибах?

2. Почему при поперечном изгибе в продольных сечениях балки возникают касательные напряжения?

3. Каким опытом можно подтвердить возникновение касатель­ных напряжений в продольных сечениях балки?

4. Напишите формулы для определения момента инерции и мо­мента сопротивления для прямоугольника. Что характеризуют эти величины? Укажите единицы измерения этих величин.

5. Напишите условие прочности при изгибе.

Содержание отчета:

18. Схема балки в масштабе

19. Решение

20. Ответы на контрольные вопросы

21. Вывод.

Приложение А

(справочное)

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Омский государственный университет путей сообщения»

структурное подразделение среднего профессионального образования

«Омский техникум железнодорожного транспорта»

(СП СПО ОТЖТ)

Специальность 23.02.06 «Техническая эксплуатация подвижного состава железных дорог»

Практическая работа №4

Расчеты на прочность при изгибе

ДисциплинаТехническая механика

Студент гр.ЭТХ – 143 - 2

(номер группы, курс)

__________________ Мишин И.В.

(подпись студента) (И., О., Фамилия студента)

________________

(дата)

Преподаватель

_____________________ Попова Е. А.

(подпись преподавателя)(И., О., Фамилия преподавателя)

______________

(дата)

__________________________________

(оценка)

Омск 2015

Цель работы–научиться строить эпюры поперечных сил и изгибающих моментов.

Задание: На балку действуют сосредоточенные силыF₁ и F₂. Построить эпюры поперечных сил и изгибающих моментов.

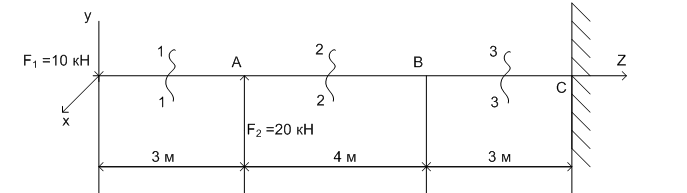
Решение:

1) рассмотрим участок до точки А с сечением 1-1.

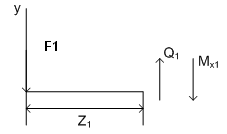
у = 0;

- F1 + Q1 = 0;

Q1+ F1;

Q1 = - 10 кН

Сила 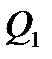- отрицательная.

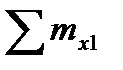= 0;

- F1z1 + Mx1=0;

Mx1 = F1z1

Mx – отрицательный

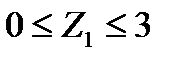
При Z1 = 0; Mx0=0

При 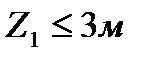; Мха = - 30 кН

Изгибающий момент меняется по линейному закону, график – прямая линия.

2) рассмотрим участок до точки В с сечением 2-2.

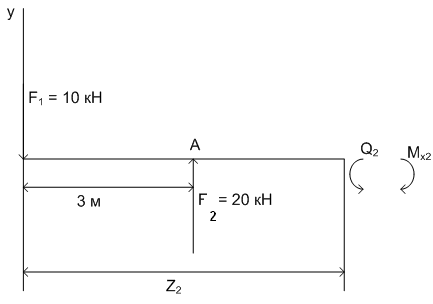
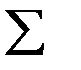Fy = 0;

- F1 + F2 - Q2 = 0

Q2 = - F1 + F2

Q2 = -10 +20 = 10 кН

Сила 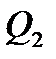положительна.

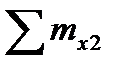= 0

- F1z2 + F2 (Z2 - 3) + Mx2 = 0

- Mx2 = F1z2 - F2 (Z2 - 3)

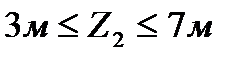
При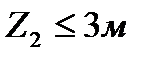

Мха = 10 * 3 = 30 кНм

Мх - отрицательный

При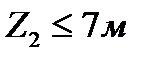

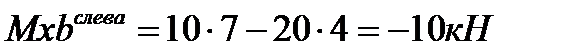
Знак меняется 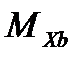слева от сечения В – положительный

Поперечную силу и изгибающий моментом определить сразу из зависимостей 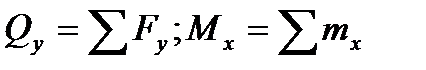, не составляя уравнения равновесия участка.

3) рассмотрим участок до точки С с сечением 3- 3.

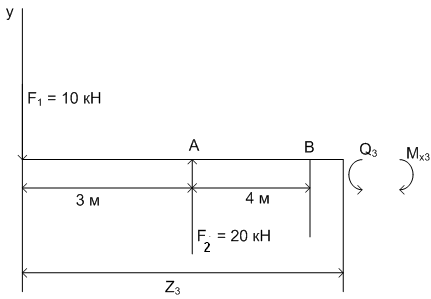
Q3 = - 10 + 20 = 10 кН – положительна

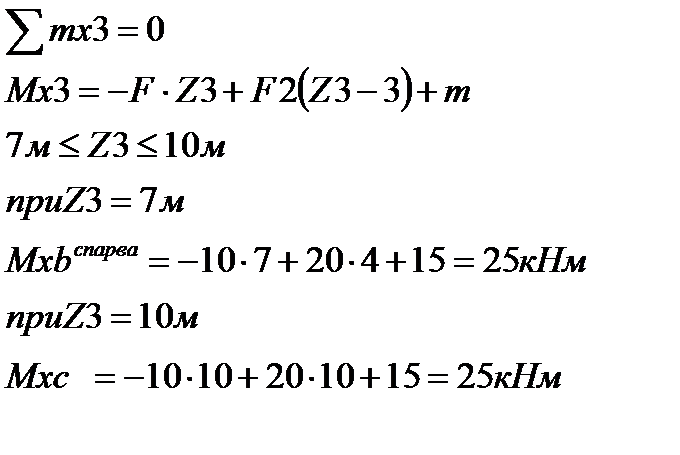
Для точки В получено два значения изгибающих моментов: из уравнения для участка 2 левее точки В и из уравнения для участка 3 правее точки В.

График поперечной силы участке 3 – прямая линия.

По полученным данным строим эпюры поперечных сил и изгибающих моментов.

Ответы на контрольные вопросы:

1 Изгибом называется вид нагружения, при котором в поперечном сечении бруса возникает силовой фактор - изгибающий момент.

2 Правило знаков поперечных сил и изгибающих моментов:

Поперечная сила в сечении считается положительной, если она стремиться развернуть сечение по часовой стрелке, если против,- отрицательной.

Если девствующие на участке внешние силы стремиться изогнуть балку выпуклостью вниз, то изгибающий момент считается положительным если наоборот - отрицательным.

3Внутренние силовые факторы при изгибе:

При чистом изгибе в поперечном сечении балки возникает только изгибающий момент, постоянный по величине.

При поперечном изгибе в сечение возникает изгиб, момент и поперечная сила.

Изгибающий момент в произвольном сечении балки численно равен алгебраической суме моментов всех внешних сил, приложенных к отсеченной части, относительно рассматриваемого сечения.

Поперечная сила в произвольном сечении балки численно равна алгебраической суме проекций всех внешних сил, действующих на отсеченной части на соответствующую ось.