Критерий дифференцируемости функции

Для того чтобы функция f являлась дифференцируемой в данной точке x₀, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

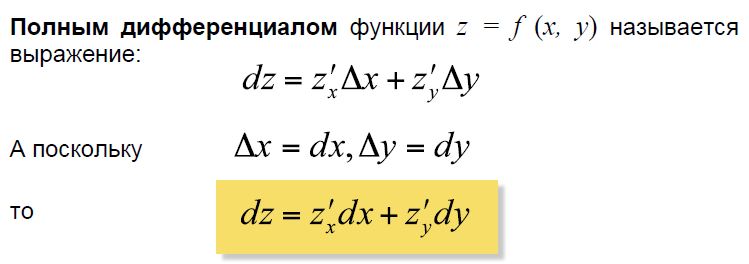
Его приложения.

Полным дифференциалом функции нескольких переменных можно пользоваться для приближённых вычислений.

Частное дифференцирование сложной функции.

В математическом анализе частная производная — одно из обобщений понятия производной на случай функции нескольких переменных.

Инвариантность формы 1-го дифференциала ФНП.

Дифференцирование неявно заданных функций.

Производная функции, заданной неявно - (для справки)

Или короче – производная неявной функции. Что такое неявная функция? Поскольку мои уроки носят практическую направленность, я стараюсь избегать определений, формулировок теорем, но здесь это будет уместно сделать. А что такое вообще функция?

Функция одной переменной 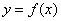–это правило, по которому каждому значению независимой переменной 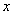соответствует одно и только одно значение функции .

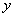Переменная 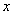называется независимой переменной или аргументом.
Переменная 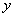называется зависимой переменной или функцией.

Грубо говоря, буковка «игрек» в данном случае – и есть функция.

До сих пор мы рассматривали функции, заданные в явном виде. Что это значит? Устроим разбор полётов на конкретных примерах.

Рассмотрим функцию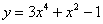

Мы видим, что слева у нас одинокий «игрек» (функция), а справа – только «иксы». То есть, функция 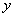в явном виде выражена через независимую переменную .

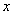Рассмотрим другую функцию: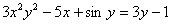

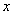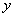Здесь переменные и расположены «вперемешку». Причем никакими способами невозможно выразить «игрек» только через «икс». Что это за способы? Перенос слагаемых из части в часть со сменой знака, вынесение за скобки, перекидывание множителей по правилу пропорции и др. Перепишите равенство 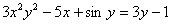и попробуйте выразить «игрек» в явном виде: 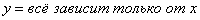. Можно крутить-вертеть уравнение часами, но у вас этого не получится.

Разрешите познакомить: 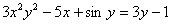– пример неявной функции.

В курсе математического анализа доказано, что неявная функция существует (однако не всегда), у неё есть график (точно так же, как и у «нормальной» функции). У неявной функции точно так же существует первая производная, вторая производная и т.д. Как говорится, все права секс-меньшинств соблюдены.

И на этом уроке мы научимся находить производную от функции, заданной неявно. Это не так сложно! Все правила дифференцирования, таблица производных элементарных функций остаются в силе. Разница в одном своеобразном моменте, который мы рассмотрим прямо сейчас.

Да, и сообщу хорошую новость – рассмотренные ниже задания выполняются по довольно жесткому и чёткому алгоритму без камня перед тремя дорожками.

Пример 1

Найти производную от функции, заданной неявно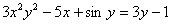

1) На первом этапе навешиваем штрихи на обе части:

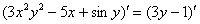
2) Используем правила линейности производной :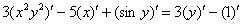

3) Непосредственное дифференцирование.
Как дифференцировать 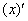и 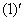совершенно понятно. Что делать там, где под штрихами есть «игреки»?

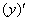– просто до безобразия, производная от функции равна её производной: .

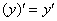Как дифференцировать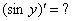
Здесь у нас сложная функция. Почему? Вроде бы под синусом всего одна буква «игрек». Но, дело в том, что всего одна буква «игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ ФУНКЦИЕЙ.Таким образом, синус – внешняя функция, 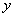– внутренняя функция. Используем правило дифференцирования сложной функции :

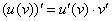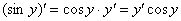
Произведение дифференцируем по обычному правилу :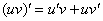

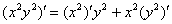
Обратите внимание, что 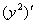– тоже сложная функция, любой «игрек с наворотами» – сложная функция:

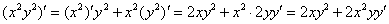
Само оформление решения должно выглядеть примерно так:


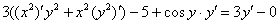
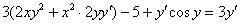
Если есть скобки, то раскрываем их:

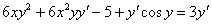
4) В левой части собираем слагаемые, в которых есть «игрек» со штрихом. В правую часть – переносим всё остальное:

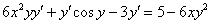
5) В левой части выносим производную 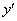за скобки:

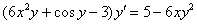
6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:

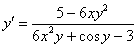
Производная найдена. Готово.

Интересно отметить, что в неявном виде можно переписать любую функцию. Например, функцию 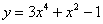можно переписать так: 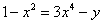. И дифференцировать её по только что рассмотренному алгоритму. На самом деле фразы «функция, заданная в неявном виде» и «неявная функция» отличаются одним смысловым нюансом. Фраза «функция, заданная в неявном виде» более общая и корректная, 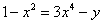– эта функция задана в неявном виде, но здесь можно выразить «игрек» и представить функцию в явном виде. Под фразой «неявная функция» понимают «классическую» неявную функцию, когда «игрек» выразить нельзя.

Второй способ решения

Внимание! Со вторым способом можно ознакомиться только в том случае, если Вы умеете уверенно находить частные производные. Начинающие изучать математический анализ и чайники, пожалуйста, не читайте и пропустите этот пункт, иначе в голове будет полная каша.

Найдем производную неявной функции 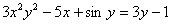вторым способом.

Переносим все слагаемые в левую часть:

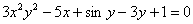
И рассматриваем функцию двух переменных:

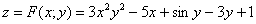
Тогда нашу производную можно найти по формуле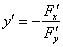
Найдем частные производные:

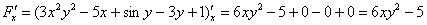
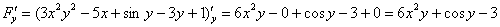
Таким образом:

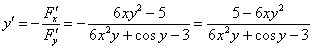
Производные и дифференциалы высших порядков.

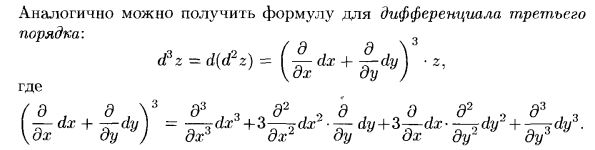
Теорема о равенстве смешанных производных.

Формула Тейлора.

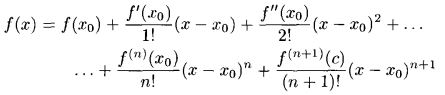26.3

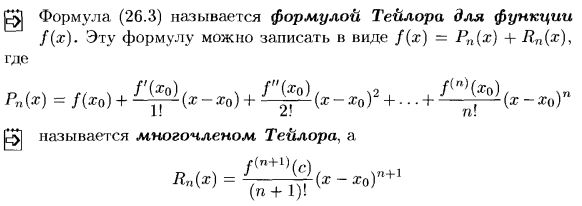
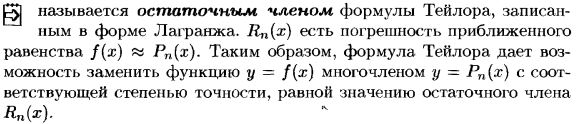
Балет №3

Производная по направлению.

В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.

Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.

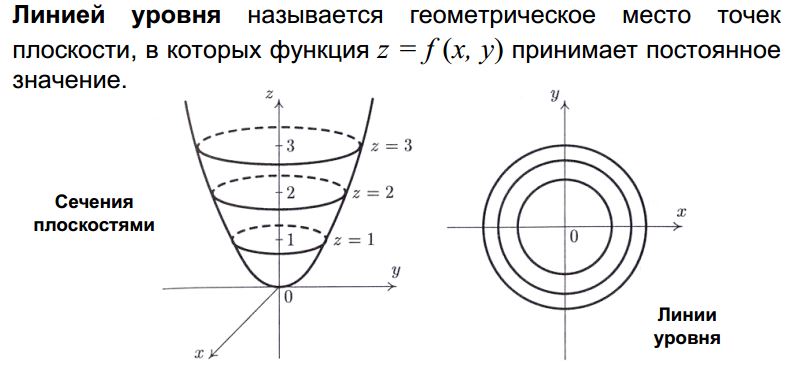
Градиент и линии уровня

Или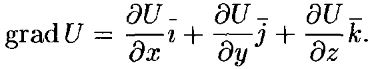

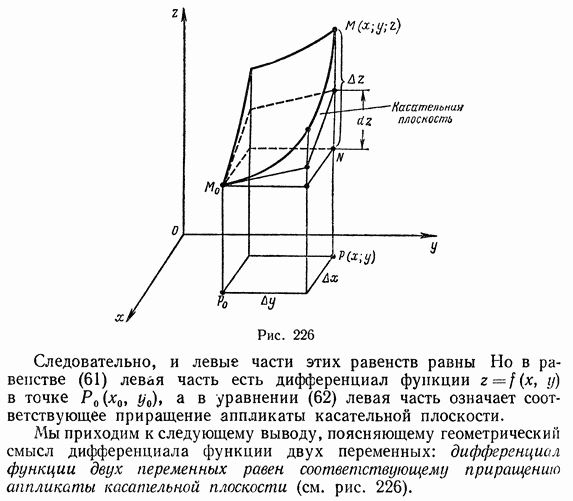
Касательная плоскость и нормаль к поверхности.

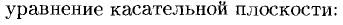
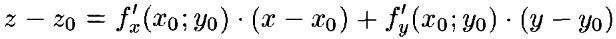
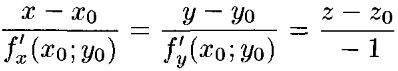
Балет №4

Локальный экстремум ФДП.

Необходимое условие локального экстремума.

Классификация кривых 2-го порядка и достаточные условия локального экстремума.

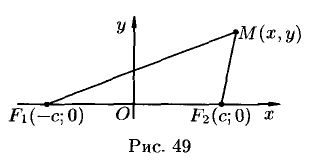
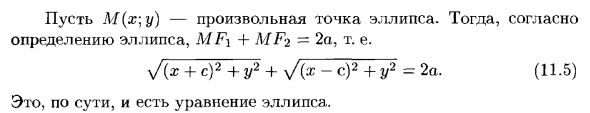
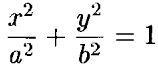Каноническое уравнение эллипса

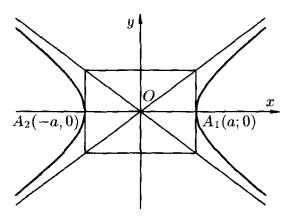
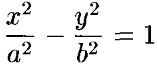Каноническое уравнение гиперболы

где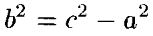

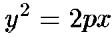Каноническое уравнение параболы

Обобщение на случай нескольких переменных, матрицы Гессе.

Матрица Гессе

Матрица этой квадратичной формы образована вторыми частными производными функции. Если все производные существуют, то

Балет №5

Условный экстремум ФДП и геометрический смысл его необходимого условия.

Условным экстремумом функции z=f(x,y) в точке M0(x0;y0) называется экстремум этой функции, достигнутый при условии, что переменные x и y в окрестности данной точки удовлетворяют уравнению связи φ(x,y)=0. Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие φ(x,y)=0.