Условие коллинеарности векторов в координатной форме

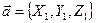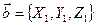Пусть и - коллинеарные векторы. Тогда .

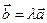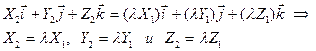(5.6)

Т.е. векторному равенству соответствует три равенства (5.6) для координат. Если векторы пропорциональны, то из (5.6) следует пропорциональность их координат:

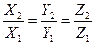
Пример 6.1.Будут ли коллинеарны векторы , ?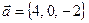

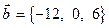Решение.Координаты векторов пропорциональны, следовательно, векторы коллинеарны, причем .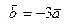

Пример 6.2. Даны векторы

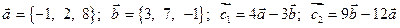. Коллинеарны ли векторы 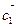и ?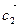

Решение.Найдем координаты векторов

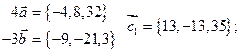
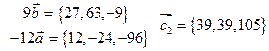
Координаты векторов не пропорциональны

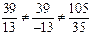
Следовательно, векторы не коллинеарны.

Деление отрезка в данном отношении.

Даны две точк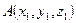и: и 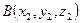. На отрезке АВ найти точку 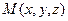, которая делит отрезок в отношении λ: 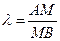. 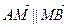, т.е. .

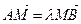Но 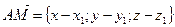и .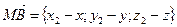

По условию коллинеарности:

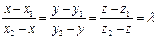. Отсюда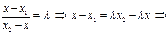

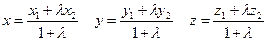(6.7)

Если λ=1, то получаем формулы деления отрезка пополам; координаты середины отрезка равны среднему арифметическому координат его концов.

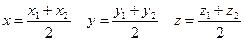(6.8)

Соответствующие формулы на плоскости получаются при 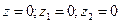из формул (6.7) и (6.8).

Пример 6.3. Даны точки А (-3, 1) и В (2, 4). В каком отношении ось Оy делит отрезок АВ?

Решение.Пусть ось Оy пересекает отрезок АВ в точке С.

Ее координаты ( 0, у). Координаты концов отрезка

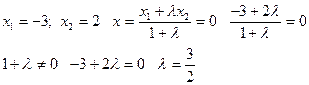
Пример 6.4Найти координаты центра масс треугольника АВС, если известны координаты его вершин: А (-4, -2); В (2, 0); С (1, 3).

Решение. Искомая точка лежит на пересечении его медиан. Найдем координаты точки D - середины стороны АВ:

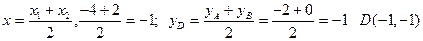
Известно, что медианы треугольника пересекаются в точке М, которая делит медиану AD в отношении1/2

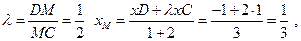
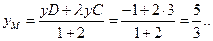
Следовательно,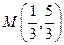

Разложение вектора по базису

Три линейно независимых вектора 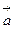, , 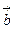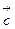образуют в пространстве базис, если любой вектор 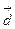может быть представлен в виде некоторой линейной комбинации векторов 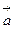, , 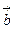, 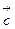т.е. для любого 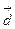найдутся такие вещественные числа 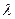, , 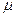, 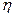что справедливо равенство:

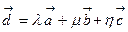(6.9)

– разложение вектора 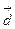по базису 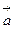, , 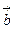, 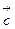где 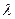, , 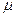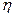- координаты 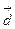относительно базиса , , .

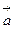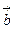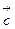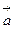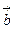Два линейно независимых вектора и образуют на плоскости базис, если любойвектор 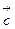может быть представлен в виде некоторой линейной комбинации векторов 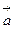и 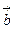, т.е. для любоговектора 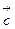найдутся такие вещественные числа 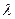, , 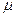что справедливо равенство:

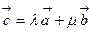(6.10)

Справедливы следующие утверждения:

1. Любая тройка некомпланарных векторов 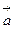, 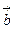и 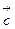образует базис в пространстве.

2. Любая пара лежащих на плоскости неколлинеарных векторов 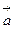и 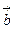образуют базис на этой плоскости.

3. Каждый вектор 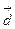может быть единственным способом разложен по базису 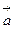, , 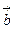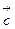или, координаты каждого вектора 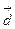относительно базиса 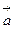, , 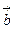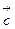определяются однозначно.

Пример 6.5. Даны векторы

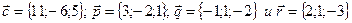
Найти разложение вектора 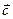по базису , , .

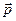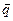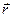Решение.Запишем разложение вектора 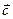по базису 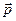, 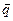и :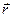

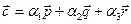. Это векторное равенство эквивалентно трем скалярным

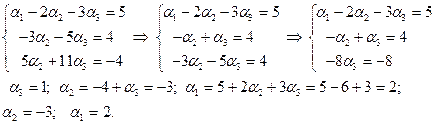Разложение вектора 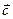по базису имеет вид: .

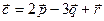Вопросы для самопроверки

1. Что называется вектором и модулем вектора?

2 .Какие векторы называют коллинеарными, компланарными, равными?

3. Могут ли два вектора, имеющие равные модули, быть неравными? Если да, то чем они отличаются друг от друга?

4. Какие операции над векторами называются линейными и каковы свойства этих операций?

5. Что называется базисом на плоскости, в пространстве?

6. Как определяется декартова система координат?

7. Как выражаются координаты вектора через координаты его начальной и конечной точек?

8. Приведите формулы деления отрезка в данном отношении