Метод эквивалентного генератора

В некоторых случаях при расчете электрической цепи нас интересуют ток, напряжение, мощность только в какой-либо одной ветви схемы. Тогда, чтобы упростить задачу и не рассчитывать всю цепь, применяют метод эквивалентного генератора.

Прежде чем перейти к методу эквивалентного генератора, докажем теорему о компенсации.

Теорема о компенсации. Любой пассивный элемент электрической цепи можно заменить активным элементом, величина ЭДС которого равна падению напряжения на пассивном элементе, а направление противоположно направлению тока в нем.

Докажем эквивалентность такой замены. Рассмотрим для пимера схемы (рис. 3.9, а,б).

Заменим пассивный элемент R₁ источником ЭДС Е₁.

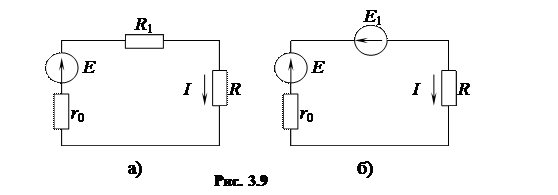Для схемы а запишем уравнение по второму закону Кирхгофа

.

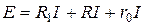Отсюда выразим ток в виде

.

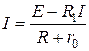Для схемы б второй закон Кирхгофа запишется в следующей форме:

.

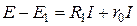Ток выразим в виде

.

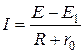При эквивалентной замене ток в сопротивлении R должен остаться неизменным, а он не изменится только в том случае, если 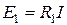, что и требовалось доказать.

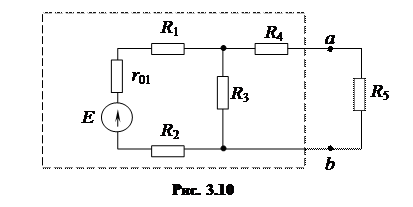
В любой электрической схеме всегда можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от ее структуры, условно изобразить прямоугольником (рис. 3.10).

Например, выделим ветвь с сопротивлением R₅, а всю остальную часть заключим в прямоугольник.

Заключенную в прямоугольник часть схемы, которая двумя выводами подключается к выделенной ветви, называют двухполюсником.

Чаще всего нас не интересует часть схемы, заключенная в двухполюснике, и его обозначают прямоугольником с двумя выводами, к которым присоединяется интересующая нас ветвь (рис. 3.11).

Если внутренняя схема двухполюсника содержит только пассивные элементы, то такой двухполюсник называется пассивным и в прямоугольнике ставится буква П, если внутренняя схема двухполюсника содержит активные элементы, то есть источники ЭДС или тока, то такой двухполюсник называется активным и в прямоугольнике ставится буква А.

Внутреннюю схему двухполюсника всегда можно разбить на участки, и эти участки, пользуясь теоремой о компенсации, заменить эквивалентными источниками. Тогда двухполюсник по отношению к выделенной ветви будет представлять собой некоторый эквивалентный генератор (рис. 3.12).

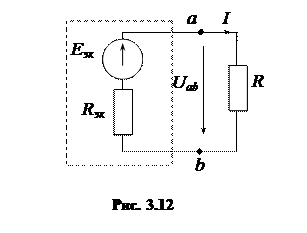Тогда ток, протекающий в выделенной ветви, можно определить, используя формулу

.

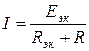Таким образом, всякий активный двухполюсник может быть заменен эквивалентным генератором с ЭДС Е_эк и внутренним сопротивлением R_эк. Для того чтобы токораспределение во внешней цепи не изменилось, должны соблюдаться следующие требования:

1) ЭДС эквивалентного генератора Е_эк равна напряжению на зажимах ab двухполюсника при холостом ходе Е_эк= U_abxx;

2) внутреннее сопротивление эквивалентного генератора R_эк равно эквивалентному сопротивлению двухполюсника относительно зажимов ab.

Таким образом, расчет цепи методом эквивалентного генератора сводится к определению параметров эквивалентного генератора Е_эк и R_эк.

Параметры эквивалентного генератора можно определить двумя способами: экспериментальным и расчетным.

Экспериментальный способ – это единственный путь определения параметров эквивалентного генератора, если неизвестна схема соединений двухполюсника. Суть его сводится к следующему.

1. При разомкнутых зажимах ab, то есть в режиме холостого хода (R = ∞ и I = 0), измеряют напряжение на зажимах ab U_аbхх. Согласно требованию 1 U_аbхх = Е_эк.

2. При замкнутых зажимах ab, то есть в режиме короткого замыкания (R = 0), измеряют ток в выделенной ветви I_кз (это можно сделать, отсоединив сопротивление R и подключив к зажимам ab амперметр, сопротивление которого мало, поэтому его можно считать замыкающим проводником).

Ток короткого замыкания связан с ЭДС источника соотношением

,

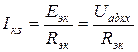отсюда

.

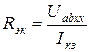Расчетный способ применяется тогда, когда известна схема внутренних соединений двухполюсника и параметры входящих в нее сопротивлений и ЭДС. Рассмотрим этот способ на конкретном примере (рис. 3.13).

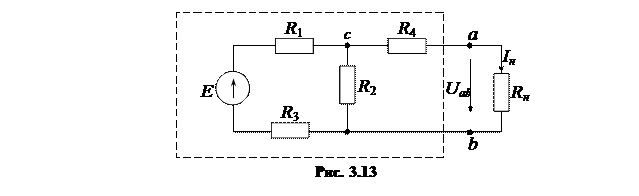Выделяем нагрузочную ветвь с сопротивлением R_н, заключая остальную часть схемы в прямоугольник. Эта часть схемы представляет собой двухполюсник с зажимами ab.

Мысленно закоротив источник ЭДС, находим эквивалентное сопротивление двухполюсника по отношению к зажимам ab, которое согласно требованию 2 равно внутреннему сопротивлению эквивалентного генератора:

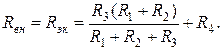
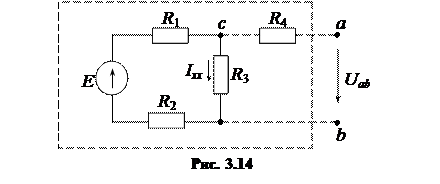3. Определим ЭДС эквивалентного генератора Е_эк, равную напряжению на зажимах ab при холостом ходе. Для этого отсоединим сопротивление нагрузки, схема примет вид (рис. 3.14).

Так как ветвь с сопротивлением R₄ разомкнута, ток будет протекать только по контуру R₁→ R₃ → R₂, то есть

.

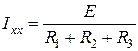Напряжение на зажимах ab будет равно напряжению на зажимах cb:

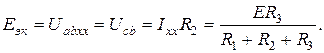
Зная R_эк и Е_эк, находим ток в нагрузке

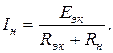
Нагрузка эквивалентного генератора согласно закону Джоуля – Ленца потребляет мощность, определяемую выражением

.

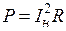В режиме холостого хода ток равен нулю, следовательно, потребляемая мощность равна нулю. В режиме короткого замыкания нулю равно сопротивление нагрузки, следовательно, мощность так же не потребляется Р = 0. Таким образом, следует предположить, что в нагрузочном режиме с ростом сопротивления нагрузки мощность сначала увеличивается до некоторого максимального значения, а потом спадает до нуля (рис. 3.15).

Найдем условие, при котором нагрузка эквивалентного генератора потребляет максимальную мощность.

Мощность в нагрузке согласно закону Джоуля – Ленца определяется выражением

.

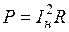Ток в нагрузке

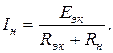
Подставим выражение для тока в формулу мощности:

.

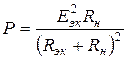Исследуем это выражение на экстремум. Функция имеет экстремум при условии равенства нулю ее первой производной.

.

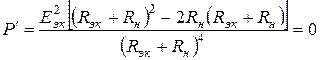Дробь равна нулю, если равен нулю числитель:

.

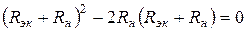Преобразуем это выражение следующим образом:

.

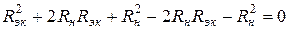Отсюда получаем .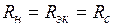

Взяв вторую производную, можно доказать, что она отрицательна, следовательно, мощность максимальна при сопротивлении нагрузки, равном сопротивлению эквивалентного генератора. Такое сопротивление нагрузки R_c называется согласованным.

Максимальную мощность можно определить по формуле

.

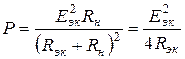На рис. 3.15 показано изменение мощности, потребляемой нагрузкой при изменении сопротивления нагрузки от нуля до бесконечности.

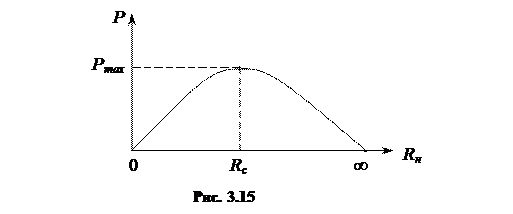Контрольные вопросы и задания

1. Дайте определение простых и сложных цепей.

2. Опишите порядок расчета простых цепей методом эквивалентных преобразований.

3. Опишите порядок расчета простых цепей методом пропорциональных величин.

4. В чем состоит метод расчета сложных электрических цепей, основанный на прямом использовании законов Киргофа?

5. Назовите достоинства и недостатки этого метода.

6. В чем состоит метод контурных токов?

7. Как определить собственные и взаимные сопротивления?

8. Поясните правило знаков при определении истинных токов по известным контурным токам.

9. Назовите достоинства и недостатки метода контурных токов.

10. В чем состоит метод узловых потенциалов?

11. Назовите достоинства и недостатки этого метода.

12. В каком случае применим метод двух узлов?

13. Что позволяет определить этот метод?

14. В чем состоит метод наложения?

15. Как при расчетах электрической цепи методом наложения определить истинные токи в ветвях?

16. Сформулируйте теорему о компенсации.

17. Что называют двухполюсником?

18. Какие существуют способы определения параметров эквивалентного генератора?

19. Поясните, при каком условии в двухполюснике выделится максимальная мощность?

20. Какую нагрузку называют согласованной?