Кері матрица

Кері матрица ұғымы тек квадрат, әрі ерекше емес матрицаға тән ұғым, яғни басқа матрица үшін кері матрица ұғымы жоқ.

Анықтама. Егер 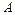матрицасы ерекше емес квадрат матрица болса, онда оған кері матрицаны 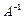түрінде белгілеп, 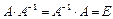теңдіктерін қанағаттандыратын матрицаны (мұндағы 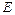матрицасы 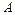матрицасымен реттес бірлік матрица) айтады.

Егер 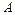матрицасы 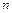-ші ретті ерекше емес матрица болса, яғни

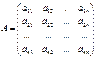
және 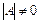, онда оған кері 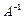матрицасы да 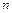-ші ретті квадрат матрица болады да, оны мына

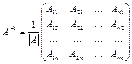
формула бойынша есептеп табады. Бұл формуладағы

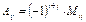
– берілген матрицасының элементінің алгебралық толықтырмасы.

МЫСАЛ.

Екі матрица берілген 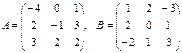. Табу керек: а) 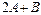; б)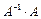

□ Матрицаны санға көбейту үшін оның әрбір элементін осы санға көбейту керек, ал матрицаларды қосу үшін (немесе азайту үшін) осы матрицалардың сәйкес элементтерін қосу керек (немесе азайту керек). Сонымен

а) .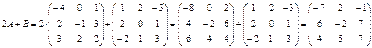

б) 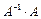көбейтіндісін табу үшін алдымен 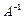кері матрицасын есептеу керек.

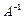кері матрицасын 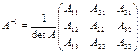формуласымен есептейміз, мұнда

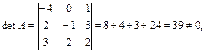
яғни 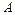– ерекшеленбеген матрица, демек оның 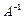кері матрицасы табылады.

Алгебралық толықтауыштарын іздестірейік:

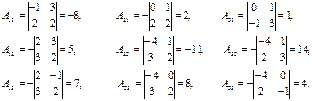
Сонда

.

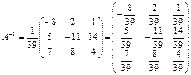Осыдан

■

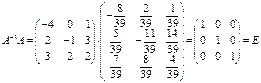Бақылау сұрақтары:

1. Симметриялы матрица деп қандай матрицаны айтады?

2. Матрицаларға қандай амалдар қолдануға болады?

3. Кері матрицаны қалай есептейді?