Уравнения Максвелла в дифференциальной форме
Интегральная форма уравнений Максвелла более наглядна, поскольку первое и второе уравнения Максвелла являются обобщениями закона полного тока и закона электромагнитной индукции. Однако для расчетов электромагнитного поля и исследования электромагнитных волн интегральная форма записи уравнений Максвелла мало пригодна. Дальнейшее обобщение приводит к необходимости описания поля в заданной точке пространства. Этого можно достичь, стягивая контур в точку, бесконечно уменьшая его размеры. При этом происходит математический переход к, так называемой, дифференциальной форме записи уравнений Максвелла.
Уравнения Максвелла могут быть представлены в дифференциальной форме:
1. 
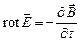; (5.9)
2. 
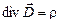; (5.10)
3. 
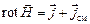; (5.11)
4. 
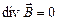. (5.12)
В данных уравнениях используются дифференциальные операторы:
Дивергенции
,
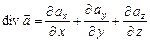и ротора
.
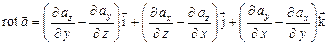Уравнения Максвелла в дифференциальной форме получаются из интегральных уравнений с помощью теорем Стокса и Гаусса, доказываемых в курсе «Высшей математики»,
,
.
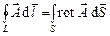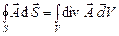Таким образом, уравнения Максвелла (5.9 – 5.12) представляют собой дифференциальные уравнения в частных производных. Их значение заключается в том, что путем их решения (интегрирования) могут быть найдены сами поля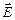 
и 
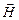в любой точке пространства.
Для полного определения уравнений Максвелла в дифференциальной форме их необходимо дополнить граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Эти условия можно сформулировать в краткой форме
; 
; 
; 
.
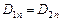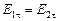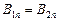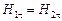Для доказательства этих соотношений рассмотрим границу раздела двух однородных магнетиков и очень малой высоты цилиндр, расположенный на границе раздела магнетиков, как показано на рис. 5.3.
Поток вектора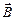 
наружу этого цилиндра можно записать в виде:
.
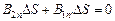Взяв обе проекции вектора 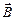на общую нормаль 
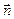, получим 
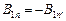, и предыдущее уравнение после сокращения на 
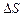примет следующий вид:
,
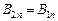т. е. нормальная составляющая вектора 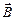оказывается одинаковой по обе стороны границы раздела. Эта величина скачка не испытывает.
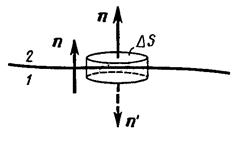
Рис. 5.3
Теперь рассмотрим ситуацию, при которой вдоль поверхности раздела течет поверхностный ток проводимости с линейной плотностью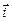 
. Применим теорему о циркуляции вектора 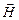к очень малому прямоугольному контуру, высота которого пренебрежимо мала по сравнению с его длиной 
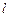, расположив этот контур так, как показано на рисунке (5.4). Пренебрегая вкладом в циркуляцию на боковых сторонах контура, запишем для всего контура:
,
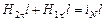где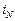 
‑ проекция вектора 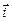на нормаль N к контуру. Взяв обе проекции вектора 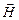на общий орт касательной 
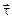(в среде 2), получим 
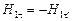, и после сокращения на 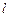предыдущее уравнение примет вид
,
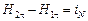т. е. тангенциальная составляющая вектора 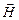при переходе границы раздела магнетиков претерпевает скачок, связанный с наличием поверхностных токов проводимости.
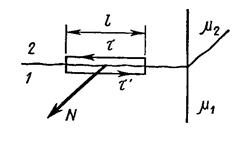
Рис. 5.4
Если на границе раздела магнетиков проводимости нет ( 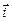=0), то тангенциальная составляющая вектора 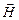оказывается одинаковой по обе стороны границы раздела:
.
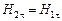Таким образом, если на границе раздела нет токов проводимости, то при переходе через границу составляющие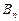 
и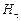 
изменяются непрерывно, без скачка. Составляющие же 
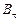и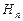 
при этом претерпевают скачок.
Аналогично можно получить условия для вектора электрической напряженности и индукции на границе двух диэлектриков
Также фундаментальные уравнения Максвелла в дифференциальной форме должны быть дополнены соотношениями, в которые входили бы величины, характеризующие индивидуальные свойства среды. Эти соотношения называются материальными уравнениями. В общем случае они могут быть крайне сложными, поэтому приведем материальные уравнения для случая изотропных сред, не содержащих сегнетоэлектриков и ферромагнетиков:
; 
; 
,
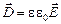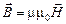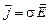где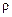 
– объемная плотность заряда; 
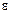– диэлектрическая проницаемость среды; 
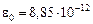Ф/м – электрическая постоянная; 
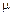– магнитная проницаемость среды; 
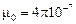Гн/м – магнитная постоянная; 
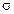– удельная электрическая проводимость среды.