Классы интегрируемых функций

1.Непрерывные функции.

Теорема 1. Всякая непрерывная на отрезке [a,b] функция интегрируема на этом отрезке.

2.Монотонные ограниченные функции и некоторые другие классы интегрируемых функций.

Теорема 2. Любая монотонная ограниченная функция является интегрируемой функцией.

Теорема 3. Любая ограниченная функция, имеющая конечное число разрывов интегрируема.

Билет 37.Замена переменной и интегрирование по частям в определенном интеграле.

Формула замены переменной. Пусть х = φ(t) непрерывна и диф. на T = {α; β}. Функция f(x) непрерывна на отрезке [a; b] = [x(α); x(β)]. Тогда ∫f(x)dx (a; b) = ∫f(φ(t))*φ’(t)dt (α; β)

Интегрирование по частям.Пусть U(x) и V(x) непрерывны и диф. на отрезке [a; b]. Тогда имеет место формула: ∫UdV = UV|_a^b - ∫VdU

Доказательство: такое же как в неопр. интеграле

Билет 38.Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.

Интеграл с переменным верхним пределом. Если функция f(x) непрерывна на [a; b], то для всех х (- [a; b] определена функция Ф(х) = ∫f(t)dt (a; x), которая называется интегралом с переменным верхним пределом. На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла.

Теорема.Если f(x) непрерывна на [a; b], то Ф’(x) = (∫f(t)dt)’ (a; x) = f(x), для всех х (- [a; b]

Формула Ньютона-Лейбница.Пусть f(x) непрерывна на [a; b], F(x) – какая либо первообразная для неё, тогда:

∫f(x)dx = F(x)|_a^b = F(b) – F(a)

Билет 39.Несобственные интегралы 1-го и 2-го рода. Сходящиеся и расходящиеся интегралы. Геометрический смысл.

Определение. При введении понятия определённого интеграла предполагали следующие условия: а) отрезок интегрирования [a; b] является конечным; б) подынтегральная функция f(x) – ограничена на отрезке интегрирования. В этом случае интеграл называется собственным. Если хотя бы одно из указанных условий нарушается, то интеграл называется несобственным, т.е. ∫f(x)dx называется несобственным, если а=-∞ или b=+∞ (или невзаимоискл.)

Сходимость / расходимость. Пусть f(x) определена и непрерывна на [a; b] (b>a). Обозначим I(b) = ∫f(x)dx, фиксируя нижний предел а. Функцию I(b) рассмотрим как интеграл с переменным верхним пределом.

1) ∫f(x)dx (a; +∞) = lim ∫f(x)dx (a;b) (bà+∞) – несобственный интеграл 1 рода на [a; +∞). Если предел в правой части существует и конечен, тогда несобственный интеграл сходится. В противном случае расходится.

2) ∫f(x)dx (-∞; b) = lim ∫f(x)dx (a;b) (aà-∞)

3) ∫f(x)dx (-∞; ∞) = ∫f(x)dx (-∞; c) + ∫f(x)dx (c; +∞) = пределы

Геометрический смысл.Пусть f(x)>0. Несобственный интеграл определяет площадь под кривой в соотв. пред., в данном случае [a; + ∞)

Несобственный интеграл 2го рода.Пусть функция f(x) задана на [a; b), не ограничена при

xàb и для любого ε>0 найдётся ∫f(x)dx (a; b-ε). Несобственным интегралом 2го рода от функции

f(x) называется lim ∫f(x)dx (a; b-ε) (εà0+) = ∫f(x)dx (a; b)

Геометрический смысл: также только площадь под графиком.

Билет 40.Свойства несобственных интегралов. Признаки сходимости. Эталонные ряды.

Свойства.1) Если сходится несобственный интеграл ∫f(x)dx (a; ∞), то найдётся такая b>a, что несобственный интеграл будет сходится и ∫f(x)dx (a; ∞) = ∫f(x)dx (b; a) + ∫f(x)dx (b; ∞)

2)Если сходятся интегралы ∫f(x)dx (a; ∞) и ∫g(x)dx (a; ∞), то сходятся и интегралы ∫(αf(x)+-βg(x))dx (a; ∞), где α и β=const и <M.

Признаки сходимости.

1) Признак сравнения. Пусть даны два несобственных интеграла ∫f(x)dx (a; ∞) и ∫g(x)dx (a; ∞), подынтегральные функции которых удовлетворяют неравенству: 0 <= f(x) <=g(x), для всех a <= x <∞. Тогда из сходимости второго интеграла следует сходимость первого, а из расходимости первого – расходимость второго.

Доказательство:

Для всех b (- (a; +∞) интеграл ∫f(x)dx (a; b) <= ∫g(x)dx (a; b). а) Перейдём к пределу при bà∞. По теореме о предельных переходах в неравенстве существует предел: lim ∫f(x)dx (a; b) (bà∞). Существование этого предела эквивалентно существованию интеграла. б) Аналогично из расходимости 1го интеграла вытекает несуществование пределов ∫f(x)dx (a; b) (bà∞) и ∫g(x)dx (a; b) (bà∞)

2) Предельный признак сравнения (эквивалентности?). Пусть существует lim f(x)/g(x) (xà+∞) = A < +∞. Тогда интегралы f(x) и g(x) сходятся или расходятся одновременно.

3) Признак Дирихле (условной сходимости). Если 1) Функции f(x) и g(x) определены в a <= x <= ∞; 2) f(x) – интегрируема в [a; A] и F(A) – ограниченная функция; 3) g(x) не возрастает и её предел при хà∞ равен нулю, то ∫f(x)g(x)dx (a; ∞) сходится

Эталонным называется интеграл, который сходится на одном промежутке, а расходится на другом.

Билет 41.Нахождение площади плоской фигуры.

1) В прямоугольных координатах.

Если непрерывная кривая задана в прямоугольных координатах уравнением y = f(x) (f(x) >= 0), то площадь криволинейной трапеции, ограниченной этой кривой двумя вертикальными прямым x=a, x=b, осью абцисс, определяется формулой S = ∫f(x)dx

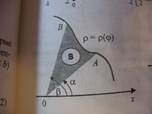
2) В полярных координатах

Если непрерывная кривая задана в полярных координатах уравнением ρ=ρ(φ), то площадь сектора AOB, ограниченная дугой кривой и двумя полярными радиусами OA и OB, выразится интегралом S = ½ ∫(ρ(φ))²dφ

3) В параметрической форме.

S = ∫ψ(t)*φ’(t)dt, где x = φ(t), y = ψ(t)

Билет 42.Нахождение объема тела вращения.

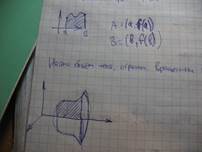a) Объём тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной кривой, заданной уравнением y = y(x), где y(x) - непрерывная однозначная функция на [a; b], осью Ох и прямыми x=a и x=b вычисляется по одной из формул: V_x = П∫f ²(x)dx (a; b) или

V_x = П ∫f ²(x)*x’(y)dy (c; d)

б) Объём тела, образованного вращением вокруг оси Оy криволинейной трапеции,

ограниченной кривой, заданной уравнением x = x(y), где x(y) - непрерывная

однозначная функция на [с; d], осью Оy и прямыми y=c и y=d вычисляется по

одной из формул: V_y = П∫f ²(y)dy (c; d) или V_y = П ∫x²*y’(x)dx

Билет 43.Длина дуги кривой.

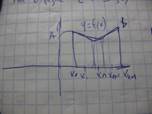
a)В прямоугольных координатах.

Пусть на [a; b] y=f(x) диффер. è непрерывна. Тогда существует предел: l = ∫корень из 1+(y’)²dx

б) В параметрической форме.

Пусть дуга задана параметрическими уравнениями x=x(t), y=y(t), x <= t <= β, то длина дуги кривой равна:

l = ∫кор. x’²(t)+y’²(t)dt, (t1; t2) – значения параметра, соответствующие концам дуги

в) В полярной системе

Если кривая задана в полярных координатах уравнением ρ=ρ(φ), φ (- [α; β], то длина дуги кривой

l = ∫корень из ρ²⁽φ)+ ρ’²(φ)dφ (α; β) – значения полярного угла в крайних точках дуги.

Билет 44.Определенный интеграл

Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где 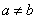) называется приращение какой-нибудь её первообразной на этом отрезке. При этом употребляется запись

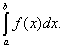
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.