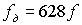Восстановление дискретизированного сигнала с помощью ряда Котельникова
Согласно теореме Котельникова непрерывный сигнал 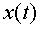 , в спектре которого не содержится частот выше
, в спектре которого не содержится частот выше 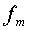 , полностью определяется последовательностью своих мгновенных значений, отсчитанных через интервал времени
, полностью определяется последовательностью своих мгновенных значений, отсчитанных через интервал времени 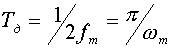 и может быть представлен рядом
и может быть представлен рядом
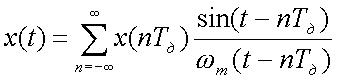 .
.
(2)
Ряд(2) называют рядом Котельникова. Если представить (2) в следующем виде:
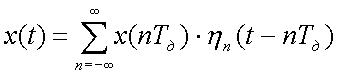 ,
,
(3)
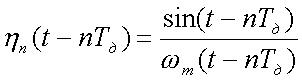 ,
,
(4)
то (в соответствии с выражением (1) 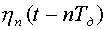 - система базисных функций, а
- система базисных функций, а 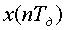 - коэффициенты ряда.
- коэффициенты ряда.
Система базисных функций ортогональна на интервале времени 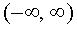 , т.е.
, т.е.
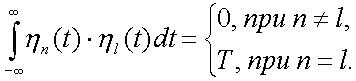
(5)
Выражение(5) – это выражение для энергии базисной функции. При 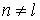 выражение (5) соответствует взаимной энергии. Т.к. взаимная энергия равна нулю, то система базисных функций ортогональна.
выражение (5) соответствует взаимной энергии. Т.к. взаимная энергия равна нулю, то система базисных функций ортогональна.
Каждая из базисных функций 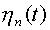 сдвинута относительно ближайшей функции
сдвинута относительно ближайшей функции 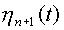 и
и 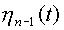 на время
на время
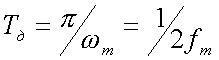 ,
,
(6)
соответствующее временному интервалу дискретизации между двумя отсчетными точками, которые иногда называют интервалом Найквиста.
Функция 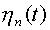 , изображенная на рис. 1. обладает свойством
, изображенная на рис. 1. обладает свойством
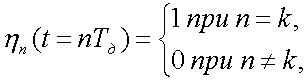
(7)
где 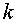 - любое целое положительное или отрицательное число.
- любое целое положительное или отрицательное число.
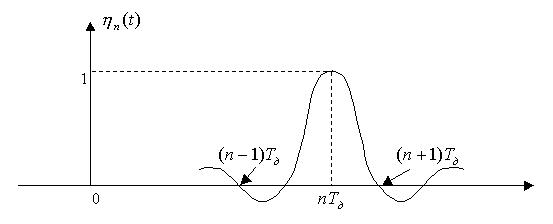
Рис. 1. График базисной функции
Рис. 2 поясняет аппроксимацию непрерывного сигнала 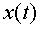 рядом Котельникова. На графике построены три члена ряда (2), соответствующие отсчетам функции
рядом Котельникова. На графике построены три члена ряда (2), соответствующие отсчетам функции 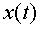 в моменты времени
в моменты времени 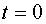 ,
, 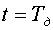 ,
, 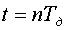 . При суммировании этих членов ряда в точках отсчетов (
. При суммировании этих членов ряда в точках отсчетов ( 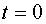 ,
, 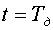 ,
, 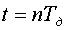 ) получаем точные значения сигнала
) получаем точные значения сигнала 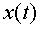 . Следовательно, в отсчетные моменты времени
. Следовательно, в отсчетные моменты времени 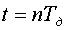 непрерывный сигнал аппроксимируется точно независимо от числа взятых отсчетов, т.е. от числа членов ряда Котельникова. Между отсчетами (
непрерывный сигнал аппроксимируется точно независимо от числа взятых отсчетов, т.е. от числа членов ряда Котельникова. Между отсчетами ( 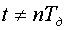 ) сигнал
) сигнал 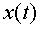 аппроксимируется точно только в том случае, когда суммируются все члены ряда (2) и соблюдается условие сформулированное в теореме Котельникова.
аппроксимируется точно только в том случае, когда суммируются все члены ряда (2) и соблюдается условие сформулированное в теореме Котельникова.
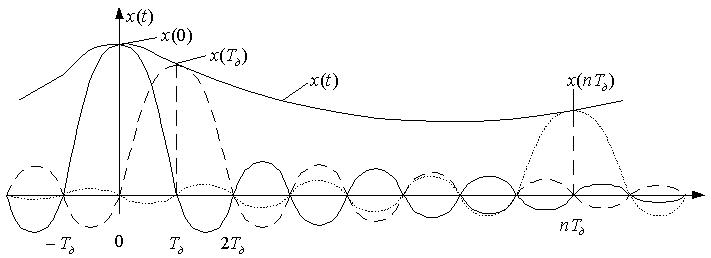
Рис. 2. Аппроксимация непрерывного сигнала рядом Котельникова
Согласно формуле (2) ряд Котельникова может использоваться для восстановления непрерывного сигнала без погрешностей. Однако в реальной ситуации погрешности возникают. Рассмотрим их источники.
На практике ряд Котельникова ограничен. Сигнал, ограниченный во времени приближенно описывается рядом (8), состоящим из конечного числа членов:
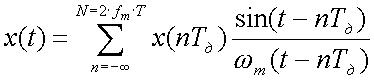 .
.
(8)
При суммировании членов ряда (8) сигнал 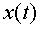 воспроизводится точно только в точках отсчетов
воспроизводится точно только в точках отсчетов 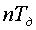 . В промежутках между отсчетами возникает погрешность аппроксимации, которая возникает у краев интервала
. В промежутках между отсчетами возникает погрешность аппроксимации, которая возникает у краев интервала 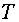 , где отброшенные члены ряда имеют наибольшее значение.
, где отброшенные члены ряда имеют наибольшее значение.
Вторым источником погрешности является то, что реальные сигналы ограничены во времени и обладают, следовательно, неограниченным по частоте спектром. Однако вне некоторой полосы частот 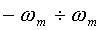 составляющие реальных сигналов обладают малой энергией по сравнению с энергией сигнала
составляющие реальных сигналов обладают малой энергией по сравнению с энергией сигнала 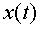 . Такие сигналы можно приближенно считать ограниченными по времени и по частоте и представлять рядом Котельникова. Это приближение является источником погрешности.
. Такие сигналы можно приближенно считать ограниченными по времени и по частоте и представлять рядом Котельникова. Это приближение является источником погрешности.
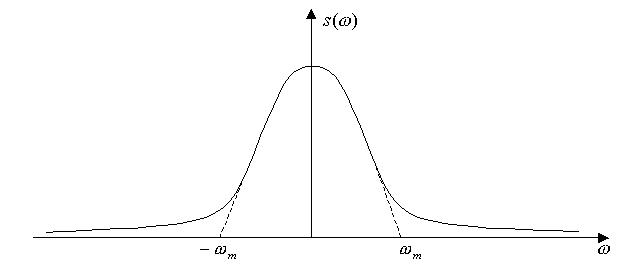
Рис. 3. Приближенное представление сигнала, ограниченного по времени и частоте
Третьим источником погрешности является неидеальность дискретизации, заключающаяся в том, что значения 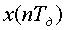 соответствует не моменту времени (функция дискретизации – последовательность дельта-функций), а небольшому интервалу с длительностью
соответствует не моменту времени (функция дискретизации – последовательность дельта-функций), а небольшому интервалу с длительностью 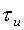 (функция дискретизации – последовательность прямоугольных импульсов).
(функция дискретизации – последовательность прямоугольных импульсов).
Восстановление дискретизированного сигнала с помощью степенных полиномов, погрешности аппроксимации, определение частоты дискретизации. Виды аппроксимации, погрешность аппроксимации
При аппроксимации сигнал 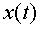 на каждом участке между его известными значениями заменяется кривой, изменяющейся по определенному закону:
на каждом участке между его известными значениями заменяется кривой, изменяющейся по определенному закону:
· горизонтальной прямой при ступенчатой аппроксимации;
·отрезком наклонной прямой при кусочно-линейной аппроксимации;
· участком параболы при параболической аппроксимации.
Разность между аппроксимированным, т.е. восстановленными и действительными промежуточными значениями функции 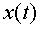 называют погрешностью аппроксимации.
называют погрешностью аппроксимации.
Таким образом погрешность аппроксимации определяется выражением
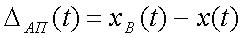
(9)
Погрешность от аппроксимации зависит от:
· скорости изменения 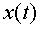 ;
;
· способа аппроксимации;
· интервала дискретизации.
Погрешность аппроксимации увеличивается с увеличением скорости изменения сигнала, уменьшается с усложнением вида аппроксимации, увеличивается с увеличением интервала дискретизации. Примеры аппроксимации приведены на рис. 4.
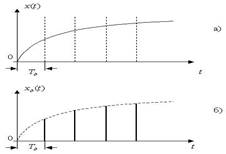
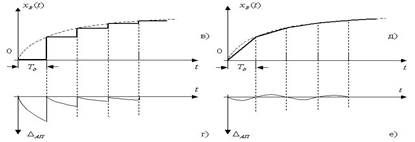
Рис. 4. Примеры аппроксимации: а) исходный сигнал; б) дискретизированный сигнал; в) сигнал, восстановленный с помощью ступенчатой аппроксимации; д) сигнал, восстановленный с помощью кусочно-линейной аппроксимации; г), е) – графики погрешностей аппроксимации.
Ступенчатая аппроксимация
При ступенчатой аппроксимации используется степенной полином нулевого порядка, т.е. аппроксимация производится отрезком горизонтальной прямой, начинающимся с момента измерения, предшествующему интервалу восстановления.
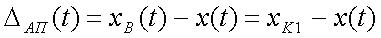 .
.
(10)
Максимальное значение погрешности от аппроксимации 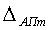 в этом случае будет на наиболее крутом участке функции, где первая производная достигает наибольшего значения.
в этом случае будет на наиболее крутом участке функции, где первая производная достигает наибольшего значения.
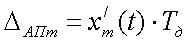 .
.
(11)
Выражение (11) может быть использовано для расчета необходимой частоты дискретизации 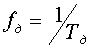 при заданной модели сигнала.
при заданной модели сигнала.
 Пример 1
Пример 1
Если принять для расчета 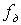 модель Берштейна, которая справедлива для стационарных случайных функций с равномерным спектром в полосе частот сигнала от
модель Берштейна, которая справедлива для стационарных случайных функций с равномерным спектром в полосе частот сигнала от 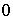 до
до 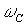 , то
, то 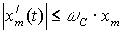 , где
, где 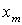 - максимальное значение амплитуды сигнала.
- максимальное значение амплитуды сигнала.
Тогда 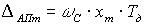 , а приведенная погрешность аппроксимации равна
, а приведенная погрешность аппроксимации равна
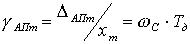 .
.
Тогда при заданной погрешности аппроксимации 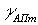 частота дискретизации равна
частота дискретизации равна
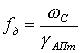 .
.
Т.е., при 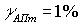
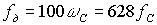 .
.
Таким образом при использовании модели Бернштейна при погрешности аппроксимации 1% частота дискретизации должна быть в 628 раз больше частоты сигнала.
 Пример 2
Пример 2
Считают, что использование модели Бернштейна приводит к завышенным требованиям к частоте дискретизации. Если принять более реальную модель, когда амплитуды гармонических составляющих с номером 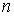 имеют амплитуду, обратно пропорциональную их номеру, то выражение для частоты дискретизации имеет вид:
имеют амплитуду, обратно пропорциональную их номеру, то выражение для частоты дискретизации имеет вид:
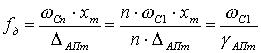 ,
,
где 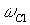 - частота первой гармоники сигнала.
- частота первой гармоники сигнала.
Для сравнения разных видов аппроксимации будем находить необходимую частоту дискретизации для одной модели сигнала – синусоидальной.
При синусоидальной модели сигнала 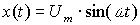
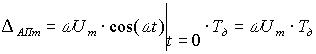 .
.
(12)
Тогда частота дискретизации 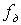 равна
равна
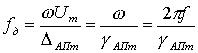 .
.
(13)
При погрешности аппроксимации 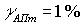 и синусоидальной модели сигнала требования к необходимой частоте дискретизации выглядит следующим образом
и синусоидальной модели сигнала требования к необходимой частоте дискретизации выглядит следующим образом