Динамика вращательного движения материальной точки и твердого тела

Краткая теория

Эффективность воздействия силы 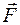на тело, которое может вращаться вокруг неподвижной оси, определяется векторным произведением:

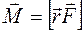, (4.1)

где 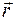- радиус-вектор точки приложения силы, 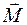- момент силы относительно оси вращения (рис. 4.1). На рис. 4.1. ось вращения проходит через точку О перпендикулярно плоскости рисунка. Модуль момента силы можно представить в виде:

,

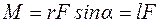где 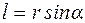- плечо силыотносительно точки О (т. е. длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила). Рисунок 4.1 выполнен в предположении, что точка О, относительно которой берется момент силы 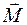, и вектор 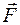лежат в плоскости рисунка. Вектор 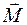перпендикулярен к плоскости рисунка и направлен от нас.

Для отдельно взятой частицы момент импульсаотносительно точки О (рис. 4.2) определяется векторным произведением:

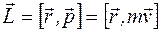, (4.2)

где 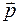- импульс частицы.Модуль вектора момента импульса можно представить в виде:

O

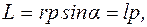
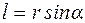где - длина перпендикуляра, опущенного из точки О на прямую, вдоль которой направлен импульс частицы. Эта длина называется плечом импульса относительно точки О.

l

Рис.4.2. Наглядное изображение момента импульса частицы массой m относительно точки О

2.1

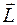Рисунок 4.2. выполнен в предположении, что точка О, относительно которой берется момент импульса , и вектор 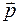лежат в плоскости рисунка. Вектор 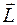перпендикулярен к плоскости рисунка и направлен от нас.

Момент инерции J материальной точки относительно оси вращения равен произведению m массы точки на квадрат расстояния r от этой точки до оси вращения:

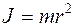. (4.3)

Момент инерции твердого тела относительно неподвижной оси называется физическая величина, характеризующая способность данного тела запасать количество вращательного движения (т. е. момента импульса ):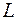

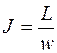, (4.4)

где w- угловая скорость. Момент инерции твердого тела относительно оси вращения зависит от распределения массы данного тела вокруг выбранной оси и может быть рассчитан по формуле:

,

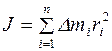где r_i – расстояние элемента массы 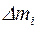от оси вращения. То же в интегральной форме:

.

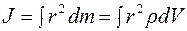Если тело однородно, т. е. его плотность 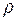одинакова по всему объему V, то:

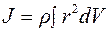. (4.5)

Моменты инерции некоторых тел правильной геометрической формы:

Тело	Ось, относительно которой определяется момент инерции	Формула момента инерции
Однородный тонкий стержень массой m и длиной l	Проходит через центр тяжести стержня перпендикулярно стержню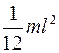
Проходит через конец стержня перпендикулярно стержню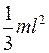
Тонкие кольцо, обруч, труба радиусом R и массой m	Проходит через центр перпендикулярно плоскости основания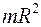
Круглый однородный диск (цилиндр) радиусом R и массой m	Проходит через центр диска перпендикулярно плоскости основания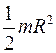
Однородный шар массой m и радиуса R	Проходит через центр шара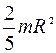

Теорема Штейнера.Момент инерции J тела относительно произвольной оси:

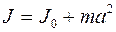, (4.6)

где J₀ – момент инерции этого тела относительно оси, проходящей через центр масс тела параллельно заданной оси; 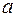- расстояние между осями; m – масса тела.

При вращении вокруг закрепленной оси выполняются законы, аналогичные первому и второму законам Ньютона для прямолинейного движения.

Первый закон Ньютона для вращательного движения:всякое тело находится в состоянии покоя или равномерного вращения c постоянной угловой скоростью 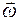, если результирующий момент сил, действующих на тело, равен нулю:

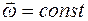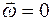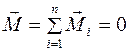( ): . (4.7)

Второй закон Ньютона для вращательного движения: под действием момента внешних сил тело приобретает угловое ускорение

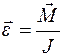, (4.8)

Основное уравнение динамики вращательного движениядля изолированной материальной точки:

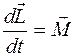, (4.9)

где 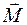- результирующий момент внешних сил, действующих на материальную точку, 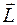- момент импульса материальной точки.

Разбив тело на элементарные массы m_i, можно представить его как систему материальных точек, взаимное расположение которых остается неизменным. Любая из этих элементарных масс может находиться под воздействием как внутренних сил, обусловленных ее взаимодействием с другими элементарными массами рассматриваемого тела, так и внешних сил. Тогда основное уравнение динамики вращательного движения для материальной точки, входящей в систему точек имеет вид:

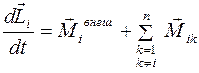, (4.10)

где 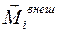- результирующий момент внешних сил, действующих на 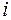-ю точку системы; 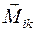- момент внутренних сил, действующих со стороны 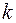-ой точки на 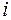-ю; n - число точек в системе; 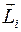-момент импульса i-ой точки, входящей в состав системы.

Основное уравнение динамики вращательного движениясистемы материальных точек:

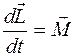, (4.11)

где 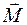= 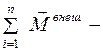главный момент внешних сил, действующих на систему материальных точек, 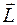= 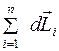-момент импульса системы точек.

Частный случай системы материальных точек – твердое тело. Для твердого тела расстояние между точками не изменяется. Поэтому уравнение (4.11) справедливо и для твердого тела. В последнем случае 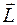есть момент импульса тела, 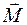- сумма моментов внешних сил, действующих на тело.

ТАБЛИЦА АНАЛОГИЙ

ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ	ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

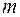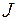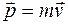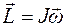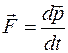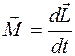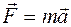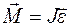Вопросы для самоподготовки

1. Назовите и запишите основные динамические характеристики вращательного движения.

2. Дайте определение момента силы относительно произвольной точки О и наглядно изобразите тройку векторов: 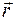- радиус-вектора точки приложения силы, 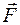- силы и 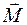- момента силы.

3. Физический маятник совершает колебания вокруг оси, проходящей через точку О перпендикулярно плоскости рисунка

4. Дайте определение момента импульса частицы относительно произвольной точки О и наглядно изобразите тройку векторов: 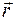- радиус-вектора частицы, 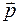- импульса частицы и 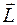- момента импульса частицы.

5. Сформулируйте определение момента инерции твердого тела относительно неподвижной оси. Что характеризует эта физическая величина?

6. Используя формулу (4.5) получите выражения для моментов инерции некоторых однородных тел правильной геометрической формы:

а) однородного тонкого стержня относительно оси, проходящей через центр тяжести стержня перпендикулярно ему;

б) однородного тонкого стержня относительно оси, проходящей через конец стержня перпендикулярно ему;

в) кольца относительно оси, проходящей через его центр перпендикулярно плоскости основания;

г) диска относительно оси, проходящей через его центр перпендикулярно плоскости основания;

д) шара относительно оси, проходящей через его центр.

7. Расскажите, как, используя теорему Штейнера, найти момент инерции тела относительно произвольной оси.

8. Сформулируйте законы Ньютона для вращательного движения.

9. Приведите примеры выполнения законов Ньютона для вращательного движения.

10. Запишите основной закон динамики вращательного движения для изолированной материальной точки, точки в системе, системы материальных точек и твердого тела.

11. Момент импульса тела относительно неподвижной оси изменяется по закону 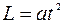. Постройте график, правильно отражающий зависимость величины М момента сил, действующих на тело, от времени.

12. Покажите аналогию между основными динамическими характеристиками поступательного и вращательного движения.

Примеры решения задач

4.1. Найти момент инерции тонкой однородной прямоугольной пластинки относительно оси, проходящей перпендикулярно к плоскости пластинки через одну из ее вершин, если стороны пластинки а и b, а ее масса m.

Дано: Найти:

a, J.

b,

m.

Решение:

Пластинка однородна, то есть ее плотность ρ одинакова по всему объему V. Тогда масса пластинки m=ρV=ρab (пластинка тонкая, поэтому ее толщину приняли за единицу).

Направим координатную ось x вдольстороны b так, как показано на рис. 4.3. Нарежем пластинку на полоски шириной dx так, чтобы центр полоски имел координату x (рис. 4.3). Масса такой полоски:

dm=ρdV=ρadx, (1)

где dV- объем полоски. Расстояние от полоски до оси перпендикулярной поверхности пластинки и проходящей через точку О равно x. Для разных полосок расстояние x меняется от 0 до b.

Момент инерции dJ полоски относительно оси перпендикулярной поверхности пластинки и проходящей через точку О может быть найден как момент инерции стержня относительно оси, проходящей через центр тяжести стержня (точку С) перпендикулярно ему, с учетом теоремы Штейнера:

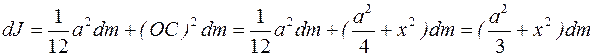. (2)

C учетом (1) выражение (2) для момента инерции полоски примет вид:

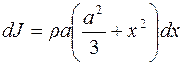. (3)

Момент инерции всей пластинки найдем интегрированием:

.

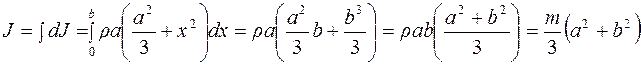Ответ: .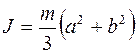

4.2.Найти момент инерции однородного сплошного конуса относительно его оси симметрии, если масса конуса m и радиус его основания R.

Дано: Найти:

R, J.

m.

Решение:

Конус однородный и сплошной, то есть его плотность ρ одинакова по всему объему V конуса. Пусть h - высота конуса (рис. 4.4), тогда с учетом формулы для объема конуса 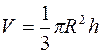его масса равна:

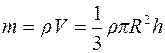. (1)

Направим координатную ось y вдоль оси симметрии конуса так, чтобы начало координат совпадало с вершиной конуса O (рис. 2.4). Нарежем конус на диски радиусом r и толщиной dy так, чтобы центр диска О^/ имел координату y. Радиус r диска может быть выражен из подобия треугольников OO^/A и OO^//B:

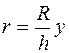. (2)

Масса dm диска радиусом r и толщиной dy с учетом выражения (2):

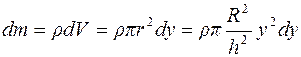. (3)

Момент инерции диска dJ относительно оси, проходящей через центр диска перпендикулярно плоскости основания, с учетом выражений (2) и (3):

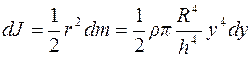. (4)

Момент инерции всего конуса найдем интегрированием:

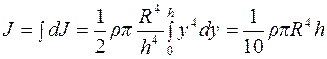. (5)

C учетом выражения (1) для массы конуса формулу (5) приведем к виду:

.

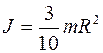Ответ: .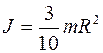

4.3.В установке (рис. 4.5) известны масса однородного сплошного цилиндра m, его радиус R и массы тел m₁ и m₂. Скольжения нити и трения в оси цилиндра нет. Найти угловое ускорение цилиндра и отношение натяжений T₁/T₂ вертикальных участков нити в процессе движения.

Дано: Найти:

m, 1. ,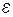

m₁, 2. T₁/T₂.

m₂,

R.

Решение:

Заданная система состоит из трех тел - грузов m₁ и m₂ и блока m. Груз m₁ находится под действием двух сил: силы тяжести 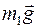и силы натяжения 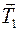нити. Второй закон Ньютона для этого груза:

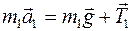. (1)

Аналогично, рассматривая силы, действующие на груз 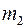, получим:

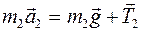. (2)

Направив ось y вертикально вниз, запишем для каждого груза уравнение движения (1) и (2) в проекциях на эту ось:

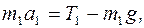(3)

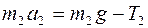, (4)

где Т₁ и Т₂ - силы натяжения нитей. 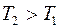: за счет этого обеспечивается вращающий момент, действующий на блок.

Ускорения обоих грузов считаем равными по модулю на основании нерастяжимости нити. Если нить не проскальзывает относительно блока, то касательное ускорение 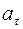его точек, соприкасающихся с нитью, равно ускорению нити в любой ее точке, а, следовательно, и ускорению грузов:

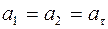
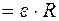, (5)

где ε - угловое ускорение цилиндра, R – радиус цилиндра. Согласно второму закону Ньютона для вращательного движения, модуль результирующего вращающего момента, приложенного к цилиндру равен:

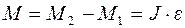, (6)

где M₁=R 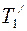, M₂=R 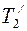(согласно уравнению (4.1.)); 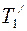и 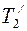- силы, приложенные к ободу цилиндра; R - плечо силы, равное радиусу цилиндра. По третьему закону Ньютона, с учетом невесомости нит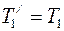и и 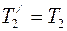. Учитывая вышесказанное, перепишем уравнение (6) в виде:

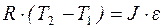. (7)

Выражая 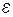=a_τ/R из соотношения (5) и учитывая, что момент инерции однородного диска 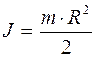, выражение (7) можно привести к виду:

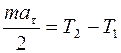. (8)

Совместное решение уравнений (3), (4), (5) и (8) относительно a_τ приводит к выражению:

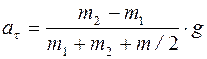. (9)

Тогда угловое ускорение цилиндра равно:

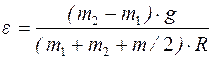. (10)

Совместное решение уравнений (3), (4), (9) дает отношение натяжений вертикальных участков нити в процессе движения:

.

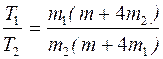Ответ: 1) 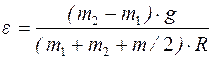, 2) .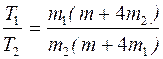

4.4.Маховик, масса которого m=5 кг можно считать распределенным по ободу радиуса r=20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр, с частотой n=720 мин^-1 (рис. 4.6). При торможении маховик останавливается через промежуток времени 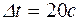. Найти тормозящий момент и число оборотов, которое сделает маховик до полной остановки.

Дано: Найти:

m=5 кг, 1. М,

r=20 см=0,2 м, 2. N.

n=720 мин^-1=12 с^-1,

.

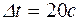Решение:

Рис. 4.6. к примеру решения задач №4.4.

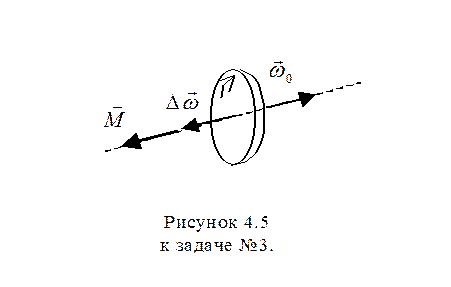
Движение маховика равнозамедленное, поэтому тормозящий момент 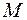постоянен и согласно второму закону Ньютона для вращательного движения равен:

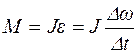, (1)

где 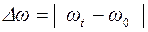- изменение угловой скорости за интервал 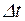. Так как в конечный момент времени угловая скорость 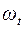=0, то изменение угловой скорости за интервал времени 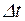равно угловой скорости 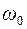в начальный момент торможения:

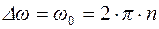. (2)

Поскольку масса маховика распределена по ободу, то его момент инерции можно найти как момент инерции кольца:

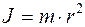. (3)

Подставив выражения (2) и (3) в (1), получим:

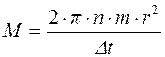=0,75 Н/м. (4)

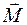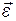Очевидно, что векторы и направлены в сторону, противоположную вектору 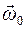. Угловое перемещение, пройденное маховиком до остановки, можно найти из уравнения равнопеременного вращательного движения:

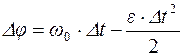. (5)

Формула зависимости угловой скорости от времени для равнозамедленного вращательного движения имеет вид:

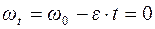. (6)

Выражая 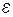из формулы (6) и подставляя в (5), получим:

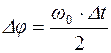. (7)

Учитывая, что 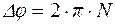и подставляя (2) в (7), можно выразить искомое число оборотов N, которое маховик сделает до полной остановки:

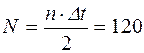об.

Ответ: 1) M=0,75 Н/м, 2) N=120 об.