Пункт 4. Правила вычисления пределов
МОДУЛЬ 2. МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
Тема 2.1. Теория пределов.
Основные понятия теории пределов.
Свойства пределов функций.
Замечательные пределы.
Правила вычисления пределов функций.
Пункт 1. Основные понятия теории пределов.
Число b называется пределом функции у = f(x) в точке а (или при х, стремящемся к а), если для всех значений х, достаточно близких к а и отличных от а, значения функции f(x) сколь угодно мало отличаются от числа b, т.е. выполняется условие |f(x) - b| < 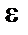 , где
, где 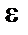 - сколь угодно малое положительное число окрестности точки а, то есть
- сколь угодно малое положительное число окрестности точки а, то есть 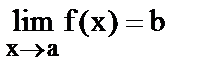 .
.
Читают: Предел функции f(x) в точке а – число b, к которому стремятся значения функции f(x), когда х стремится к а или f(x) ® b при х ® а.
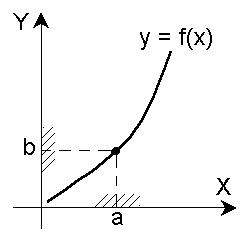
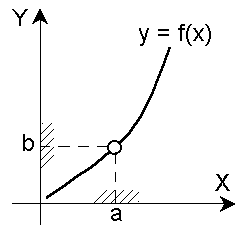
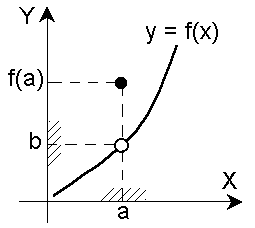
 Окрестностью точки а называется любой интервал, содержащий точку внутри себя.
Окрестностью точки а называется любой интервал, содержащий точку внутри себя.
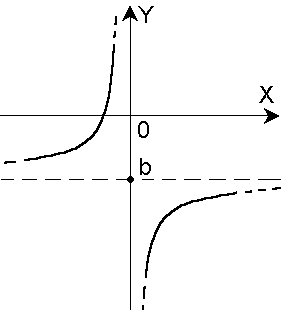
Число b называется пределом функции у = f(x) на бесконечности(или при х, стремящемся к бесконечности), если при всех достаточно больших по модулю значений аргумента х соответствующие значения функции f(x) сколь угодно мало отличаются от числа b.
Теорема о единственности предела. Если функция имеет предел при x→a, то этот предел единственный.
Пределом функции f(x) в точке хо слева (справа) называется предел, вычисляемый в предположении, что х стремится к хо, оставаясь все время меньше (больше) хо.
Пределы слева и справа называются односторонними пределами и соответственно обозначаются: 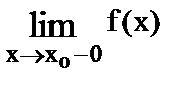 и
и 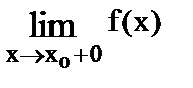 .
.
Величина f(x) называется бесконечно малой, если ее предел равен 0, то есть 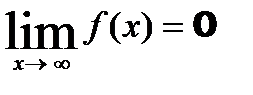 .
.
Величина называется бесконечно большой, если ее предел равен ¥, то есть 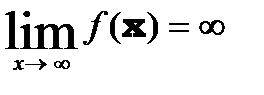 .
.
Следует отметить, что обратная бесконечно малой величины является бесконечно большой величиной и наоборот.
Пункт 2. Свойства пределов функции.
Если существуют 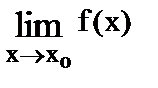 и
и 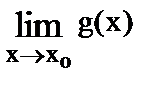 , то
, то
1. 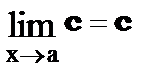 где с = const
где с = const
2. 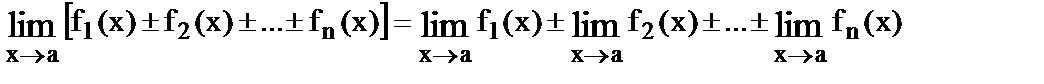
3. 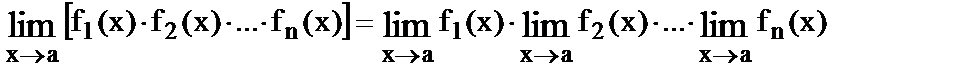
4. 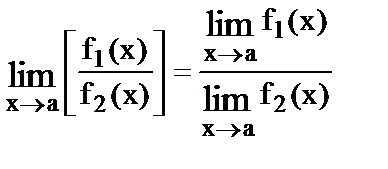 где
где 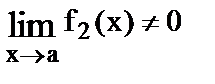
5. 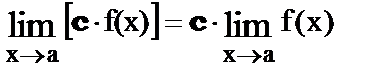 где с = const
где с = const
6.Если f1(x) £ f(x) £ f2(x) и 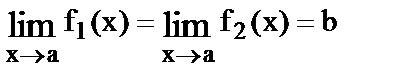 , то
, то 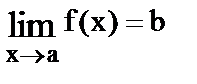
7. 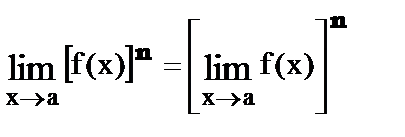
8. 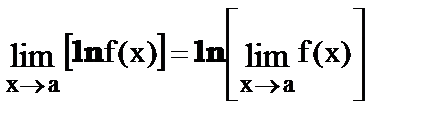
9. 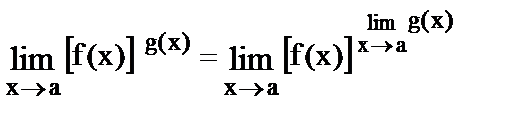 .
.
Пункт 3. Замечательные пределы.
Существует два замечательных предела, которые облегчают процесс вычисления различных пределов функций – это первый и второй замечательные пределы функций.
Первый замечательный предел функции.
 или
или 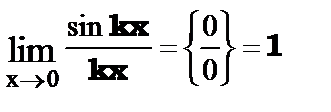 .
.
Следствия из первого замечательного предела:
Можно использовать следствия этого предела:
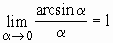 ;
; 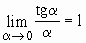 ;
; 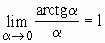 ;
; 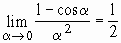
Примеры.
1. 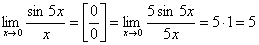 .
.
2. 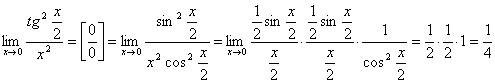 .
.
3. 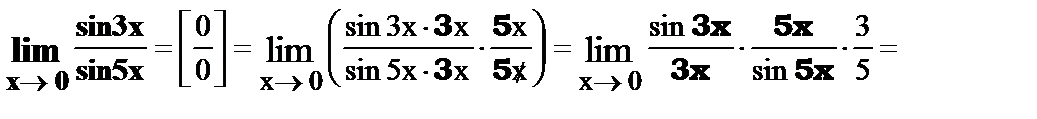
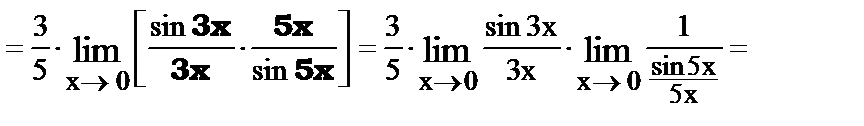
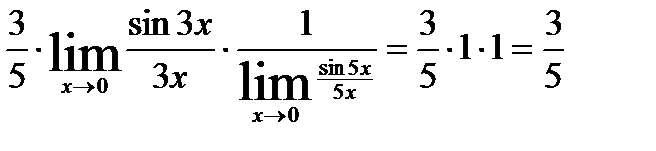
4. 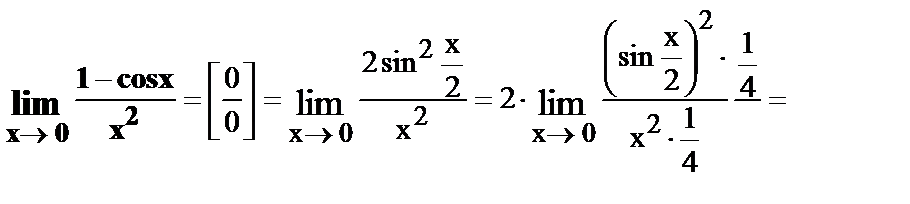
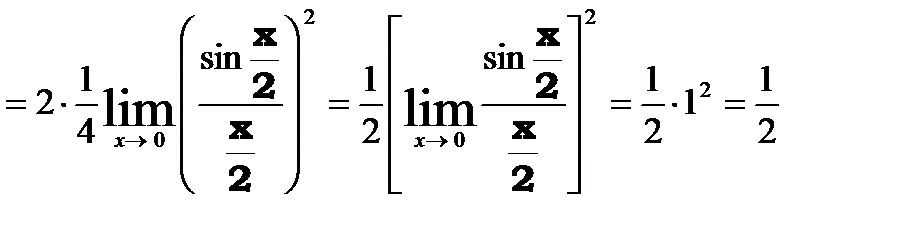 .
.
Второй замечательный предел функции.
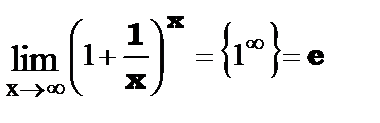 или
или 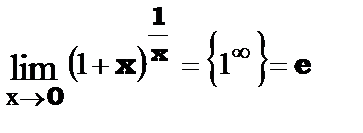 , где число е - число Эйлера и е » 2,718281…
, где число е - число Эйлера и е » 2,718281…
Примеры:
5. 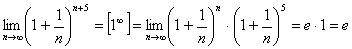 .
.
6. 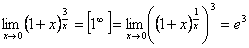 .
.
7. 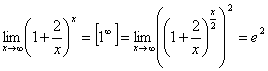 .
.
8. 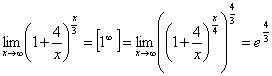
9. 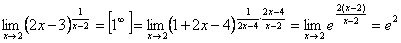 .
.
10. 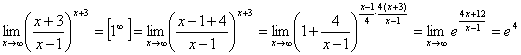
Пункт 4. Правила вычисления пределов.
При вычислении пределов различных функций могут появиться неопределенные выражения вида: 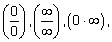
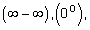
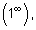
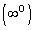 . Такие выражения называются неопределенностями. Поэтому наша задача сводится к раскрытию таких неопределенностей.
. Такие выражения называются неопределенностями. Поэтому наша задача сводится к раскрытию таких неопределенностей.
Неопределенность вида 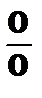 .
.
Для того, чтобы раскрыть неопределенность подобного вида, необходимы тождественные преобразования (разложение на множители, применение формул сокращенного умножения и т.д.)
Примеры.
11. 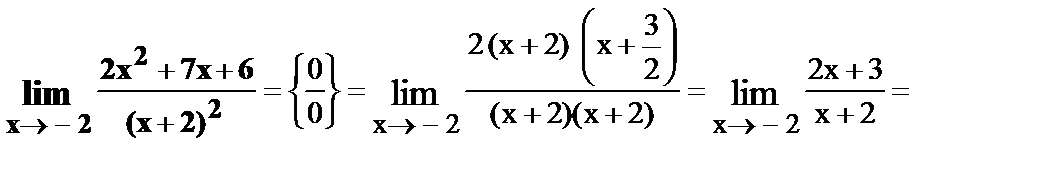
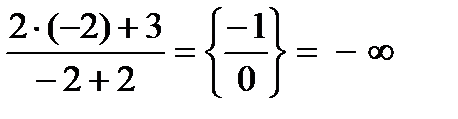
12. 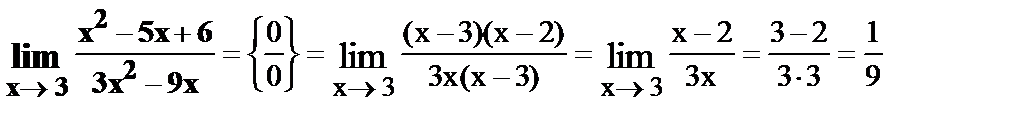
13. 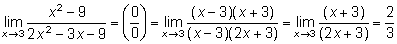
Иногда неопределенность такого вида появляется в пределах функций, содержащих знак радикала. В этом случае уничтожают иррациональность, для чего числитель и знаменатель умножают на выражение, сопряженное выражению, которое содержит иррациональность, при этом используют формулу (a – b) (a + b) = a2 – b2.
Примеры:
14. 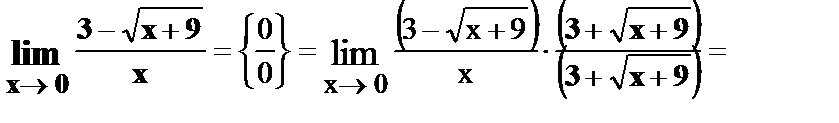
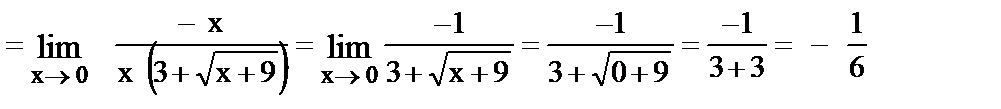
15. 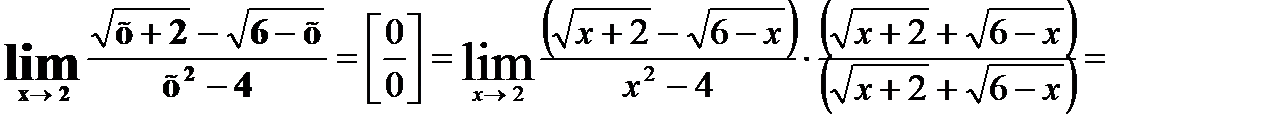
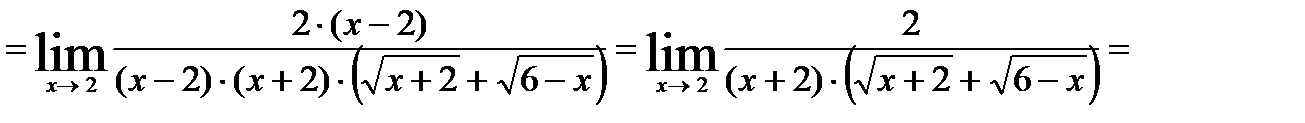
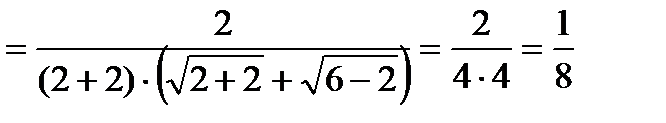
Неопределенность вида 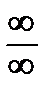 .
.
Для того, чтобы раскрыть неопределенность подобного вида, необходимо каждое слагаемой в числителе и знаменателе дроби разделить на наивысшую степень всей дроби.
Примеры:
16. 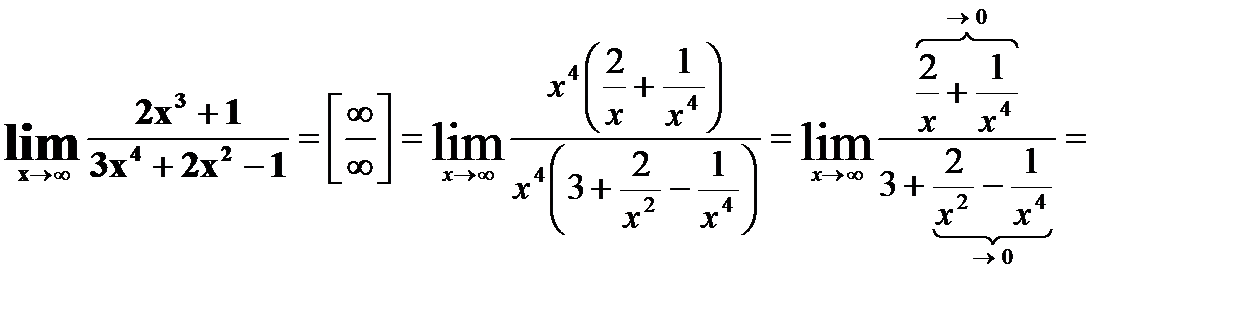
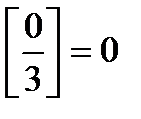
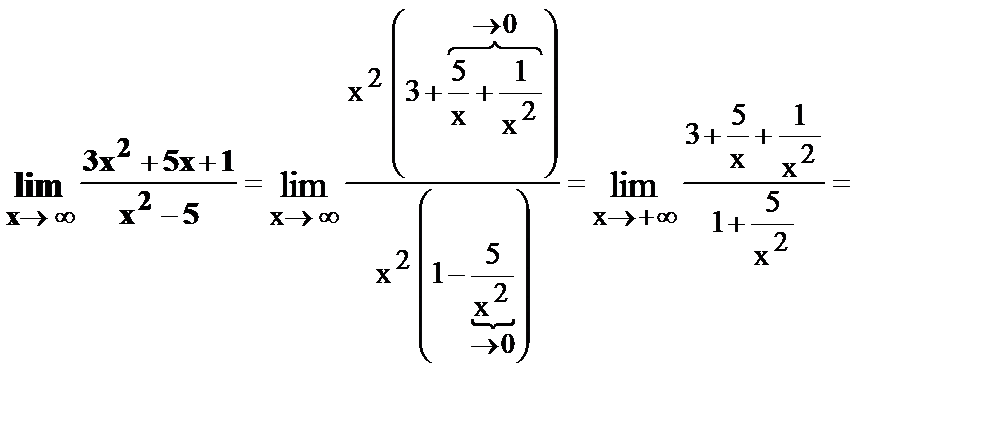
17. 
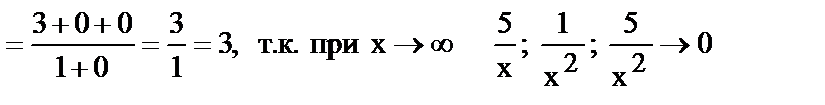
18. 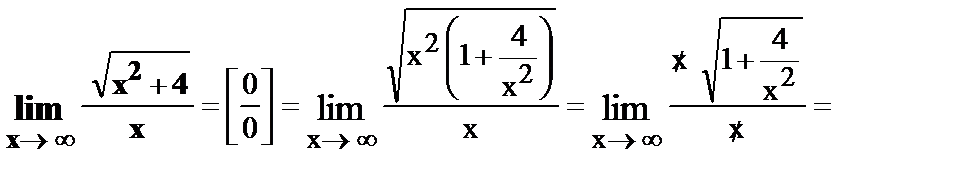
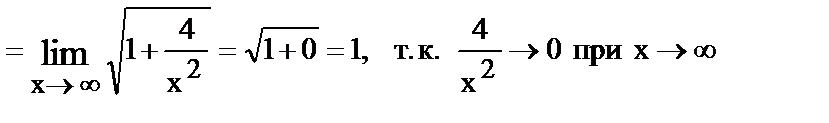
Неопределенность вида ¥ - ¥.
В этом случае нужно:
Ø выполнить вычитание дробей, сделать необходимые тождественные преобразования и свести к неопределенности вида 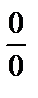 или
или 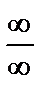
ИЛИ
Ø числитель и знаменатель одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида 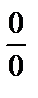 или
или 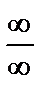
ИЛИ
Ø преобразовать соответствующую разность f1(x) – f2(x) в произведение:
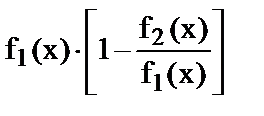 и раскрыть неопределенность
и раскрыть неопределенность 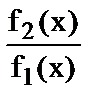 ;
; 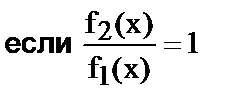 ,
, 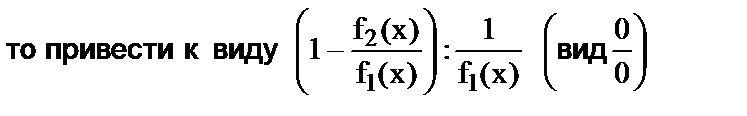 .
.
Примеры:
19. 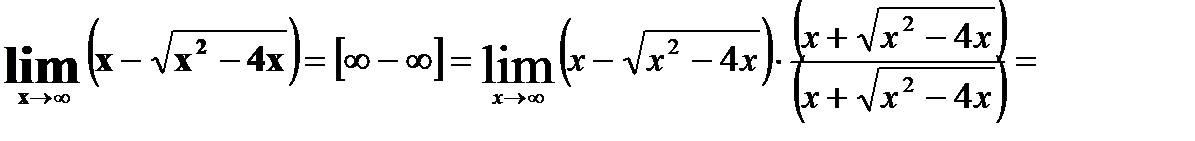
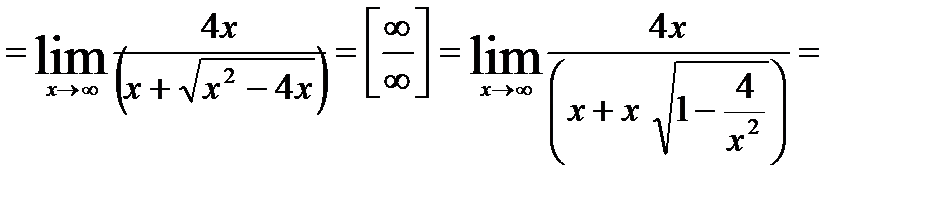
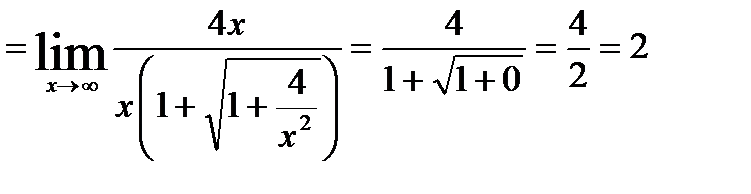
20. 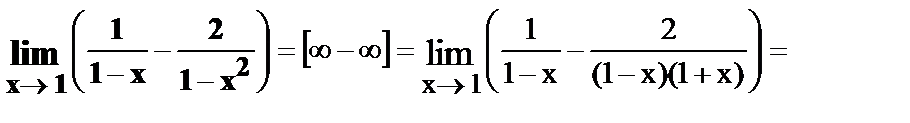
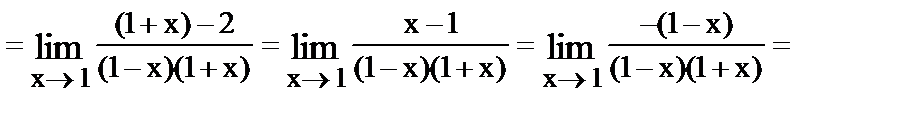
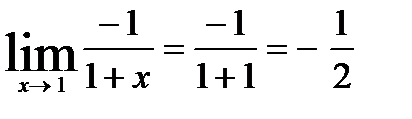
Неопределенность вида 0 × ¥ .
Для раскрытия этой неопределенности необходимо преобразовать соответствующее произведение f1(x) × f2(x), где 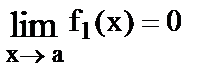 и
и 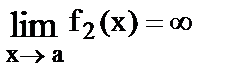 , в частное
, в частное 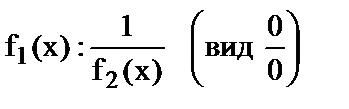 или
или 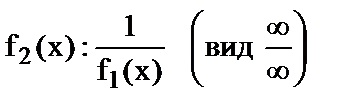 .
.
Примеры:
21. 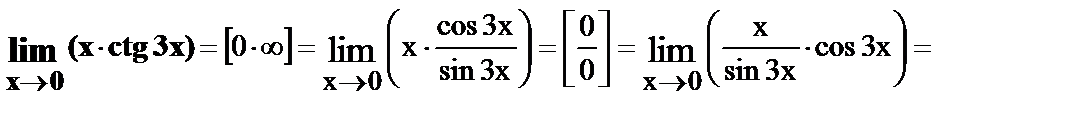
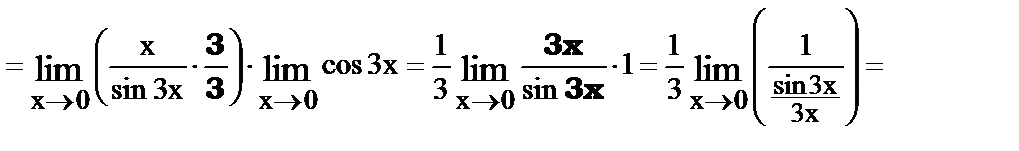
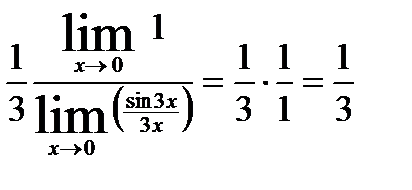 .
.
22. 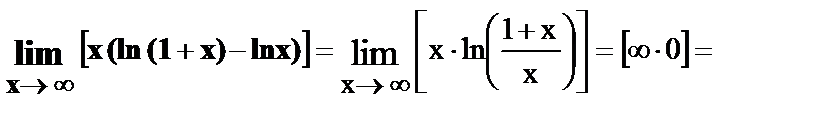
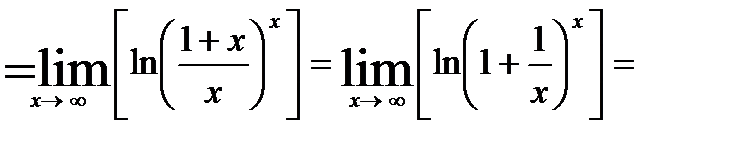
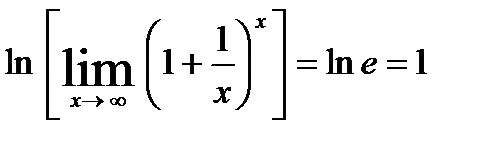 .
.
Часто для вычисления пределов любых функций используют производные функций. Это носит название правила Лопиталя.
Первое правило Лопиталя.
Если 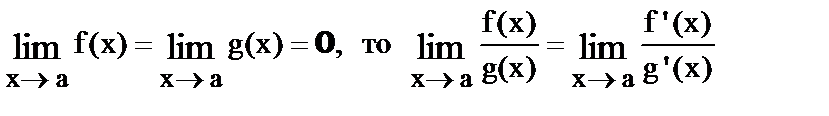 .
.
Второе правило Лопиталя.
Если 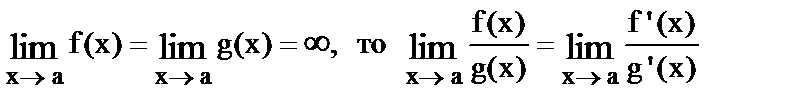 .
.
Примеры.
23. 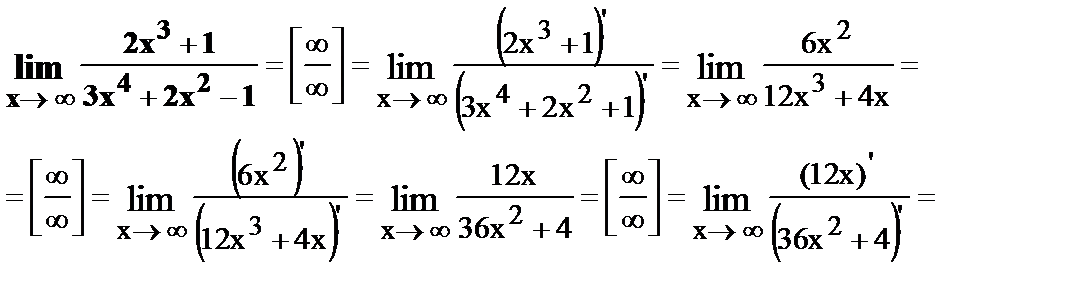
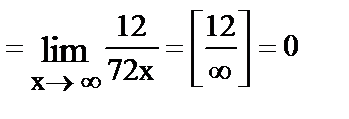
24. 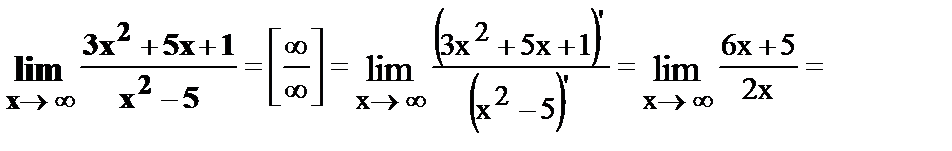
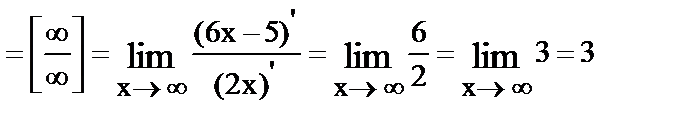
25. 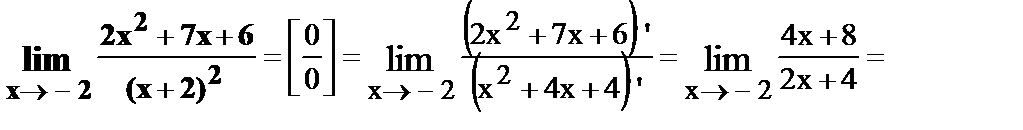
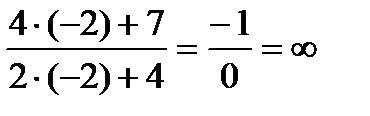 .
.
26. 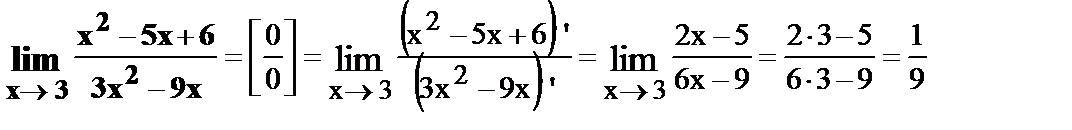 .
.
