Рнектің мәнін тап
1. Өрнектің мәнін мәнін табыңыз:
4х2 – 20х + 25, мұндағы х = 12,5
A) 625 B) 350 C) 600 D) 400 E) 80
2. –3у+5(2у–3) өрнегінің мәнін тап. у= –1,3
A) 15 B) 24,1 C) –15 D) –9,1 E) –24,1
3. 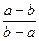 өрнегінің a = -5, b = -7 болғандағы сан мәнін табыңыз.
өрнегінің a = -5, b = -7 болғандағы сан мәнін табыңыз.
A) -6 B) 8 C) -1 D) 0 E) 17
4. 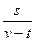 өрнегінің мәнін тап. Мұнда
өрнегінің мәнін тап. Мұнда 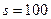 ,
, 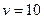 ,
, 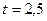 .
.
A) 12 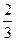 B) 10
B) 10 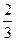 C) 13 D) 11
C) 13 D) 11 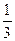 E) 13
E) 13 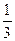
5. 4x6y3 - 3x6y3 + 2x2y2 - x6y3 - x2y2 көпмүшеліктің x = -3, y = -1 болғандағы сан мәнін табыңыз.
A) 27 B) 9 C) 19 D) 11 E) -14
6. Бөлшектін мәнін табыңыз: 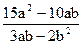 , мұндағы a =-2; b = –0,1
, мұндағы a =-2; b = –0,1
A) 100 B) 50 C) 10 D) 107 E) –43,75
7. 2(х+4)–3х өрнегінің мәнін тап, х=0,9
A) 7,9 B) 7,1 C) 12,5 D) 8,1 E) 8,9
8. (3а3x - 13x2) - (3a3x + 6x2) өрнегін ықшамдап,
а = -1 және x = 1 болғандағы сан мәнін табыңыз.
A) -19 B) 15 C) 19 D) -47 E) -21
9. 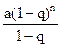 өрнегінің
өрнегінің 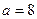 ,
, 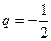 ,
, 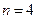 болғандағы сан мәнін табыңыз.
болғандағы сан мәнін табыңыз.
A) 0 B) -21 C) -19 D) 27 E) 17
10. Бөлшектің мәнін табыңыз: 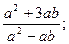 мұндағы
мұндағы 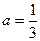 және
және 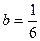 .
.
A) 5 B) 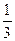 C)
C) 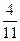 D) -5 E) 3
D) -5 E) 3
11. 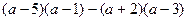 өрнегінің
өрнегінің 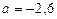 болғандағы сан мәнін табыңыз.
болғандағы сан мәнін табыңыз.
A) 24 B) -18 C) -24 D) 42 E) 53
12. Өрнектің мәнін табыңыз: 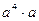 мүнда
мүнда 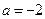
A) −8 B) −32 C) 16 D) −16 E) 32
13. Бөлшектің мәнін табыңыз: 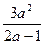 , мұнда
, мұнда  .
.
A) 3 B) -3 C) 6 D) 4 E) 2,4
14. 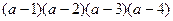 өрнегінің
өрнегінің 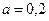 болғандағы сан мәнің табыңыз.
болғандағы сан мәнің табыңыз.
A) -120,8 B) -12,08 C) 0 D) 1,208 E) 12,08
15. Бөлшектін мәнін табыңыз: 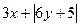 , мұндағы
, мұндағы 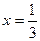 және
және 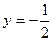
A) 1 B) -1 C) -2 D) 2 E) 3
16. Бөлшекті қысқартыңыз және сандық ьәнін табыңыз: 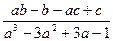 , мұндағы
, мұндағы 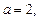
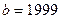 ,
, 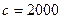 .
.
A) -2 B) -1 C) 1 D) 3 E) 2
17. Бөлшектін мәнін табыңыз: 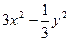
 мұндағы
мұндағы 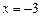 және
және 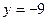
А) -54 В) -27 С) 0 D) 27 E) 54
18. Бөлшектін мәнін табыңыз: 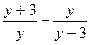 , мұндағы
, мұндағы 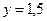 .
.
A) 6.75 B) 2 C) -4 D) 4 E) -12
19. 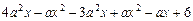 көпмүшеліктің
көпмүшеліктің 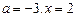 болғандағы сан мәнін табыңыз.
болғандағы сан мәнін табыңыз.
A) 30 B) 35 C)-43 D) 62 E) 39
20. 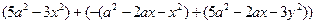
өрнегін ықшамдап 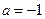 ,
, 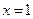 және
және  болғандағы сан мәнін табыңыз.
болғандағы сан мәнін табыңыз.
A) -11 B) 8 C) -3 D) 4 E) 32
Прогрессия 1
1. 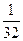 саны 4; 2; 1; ... геометриялық прогрессияның мүшесі бола ма? Болса, оның номерін көрсетіңіз.
саны 4; 2; 1; ... геометриялық прогрессияның мүшесі бола ма? Болса, оның номерін көрсетіңіз.
A) Болады, номер 8 B) Болмайды
C) Болады, номер 7 D) Болады, номер 6
E) Болады, номер 5
2. Геометриялық прогрессияның 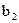 -
- 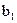 = - 4,
= - 4,
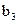 -
- 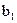 = 8 екендігі белгілі. Осы прогрессияның алғашқы бес мүшесінің қосындысын табыңыз.
= 8 екендігі белгілі. Осы прогрессияның алғашқы бес мүшесінің қосындысын табыңыз.
A) 0 B) 2 C) -20 D) 30 E) 61
3. Арифметикалық прогрессияның екінші мүшесі 18, ал оның бесінші мүшесі 9-ға тең. Прогрессияның бірінші мен алтыншы мүшесінің қосындысын табыңыз.
A) 25 B) 26 C) 27 D) 29 E) 28
4. Арифметикалық прогрессияның үшінші мен бесінші мүшелерінің қосындысы 30-ға, ал алтыншы мен бірінші мүшелерінің айырмасы 20-ға тең. Прогрессияның алғашқы сегіз мүшесінің қосындысын табыңыз.
A) 136 B) 119 C) 160 D) 153 E) 102
5. Егер a1 = 16,5; d = 1,5 болса, онда арифметикалық прогрессия құрайтын тізбектің алғашқы он екі мүшесінің қосындысын табыңыз.
A) 107,25 B) 307,25 C) 207 D) 297 E) 421
6. Геометриялық прогрессияда еселігі 3-ке, алғашқы алты мүшесінің қосындысы 1820-ға тең екендігі белгілі болса, онда бірінші және бесінші мүшелерін табыңыз.
A) b1 = 5, b5 = 405 B) b1 = 5, b5 = 80
C) b1 = 7, b5 = 567 D) b1 = 3, b5 = 768
E) b1 = 3, b5 = 48
7. Арифметикалық прогрессияның a4 = -4,
a17 = -17 екендігі белгілі. Осы прогрессияның алғашқы он жеті мүшесінің қосындысын табыңыз.
A) -154 B) -151 C) -152 D) -153 E) -150
8. Үш сан геометриялық прогрессия құрайды. Егер екінші санды 2-ге арттырса, прогрессия арифметикалық прогрессияға, ал содан кейін соңғы санды 9-ға арттырса, қайтадан геометриялық прогрессия құрайтын сандар шығады. Осы сандарды табыңыз.
A) 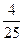 , -
, - 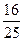 ,
, 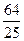 B) 1) 4, 8, 16 2)
B) 1) 4, 8, 16 2) 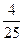 , -
, - 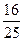 ,
, 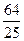
C) 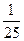 , -
, - 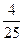 ,
, 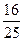 D) 1) 2, 8, 32; 2)
D) 1) 2, 8, 32; 2) 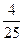 , -
, - 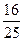 ,
, 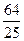
D) 4, 8, 16
9. Егер геометриялық прогрессияның еселігі 2-ге, ал алғашқы жеті мүшесінің қосындысы 635-ке тең болса, онда бірінші мүшесін табыңыз.
A) 5 B) 7 C) –6 D) 6 E) –5
10. Арифметикалық прогрессияның n = 25; аn = -12; Sn = 900 екендігі белгілі. Прогрессияның бірінші мүшесі мен айырмасын табыңыз.
A) а1=72, d= -4 B) а1=60, d= -4 C) а1=60, d= 4
D) а1=84, d= -4 E) а1=72, d= 4
11. Мүшелері оң болатын шектеусіз геометриялық прогрессияның (½q½<1) алғашқы үш мүшесінің қосындысы 10,5; ал прогрессияның қосындысы 12 тең. Прогрессияны жазыңыз.
A) 6, 2, 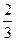 , ... B) 5, 1,
, ... B) 5, 1, 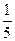 , ... C) 4, 2, 1, ...
, ... C) 4, 2, 1, ...
D) 6, 3,  , ... E) 4,
, ... E) 4, 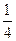 ,
, 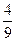 , ...
, ...
12. Егер геометриялық прогрессияның 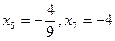 болса, онда оның еселігін табыңыз.
болса, онда оның еселігін табыңыз.
A) –3 B) 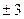 C) 3 D)
C) 3 D) 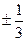 E)
E) 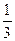
13. Екі арифметикалық прогрессия берілген. Бірінші прогрессияның бірінші және бесінші мүшелері сәйкесінше 7 және -5-ке тең. Ал екінші прогрессияның бірінші мүшесі 0, соңғы мүшесі 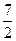 -ге тең. Екі прогрессияның да үшінші мүшелері тең болатыны белгілі болса, онда екінші прогрессияның мүшелерінің қосындысын табыңыз.
-ге тең. Екі прогрессияның да үшінші мүшелері тең болатыны белгілі болса, онда екінші прогрессияның мүшелерінің қосындысын табыңыз.
A) 18 B) 20 C) 28 D) 16 E) 14
14. Геометриялық прогрессияның алғашқы алты мүшесінің қосындысын табыңыз, оның b1 = 81;
q = 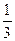 белгілі болса.
белгілі болса.
A) 30 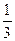 B) 364 C) 150
B) 364 C) 150 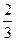 D) 121
D) 121 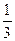 E) 60
E) 60 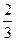
15. Барлық мүшелері оң геометриялық прогресиияның үшінші мен жетінші мүшелерінің көбейтіндісі 25-ке тең. 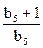 мәнін табыңыз, мұндағы b5 - прогрессияның бесінші мүшесі.
мәнін табыңыз, мұндағы b5 - прогрессияның бесінші мүшесі.
A) 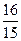 B)
B) 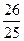 C)
C) 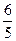 D)
D) 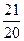 E)
E) 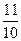
16. Егер a1 = 72; d = -6 болса, онда арифметикалық прогрессия құрайтын тізбектің алғашқы он сегіз мүшесінің қосындысын табыңыз.
A) 408 B) 378 C) 336 D) 418 E) 496
17. Геометриялық прогрессия құрайтын үш санның қосындысы 39-ға, ал олардың 3 негізіндегі логарифмдерінің қосындысы 6-ға тең. Прогрессия еселігін табыңыз.
A) q = 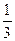 B) q = -3 немесе q = -
B) q = -3 немесе q = - 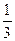 C) q = 3
C) q = 3
D) q = -3 немесе q = 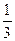 E) q = 3 немесе q =
E) q = 3 немесе q = 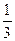
18. Бірінші мүшесі  -ге, үшінші мүшесі
-ге, үшінші мүшесі 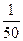 -ге, ал еселігі оң болатын геометриялық прогрессияның алғашқы бес мүшесінің қосындысын табыңыз.
-ге, ал еселігі оң болатын геометриялық прогрессияның алғашқы бес мүшесінің қосындысын табыңыз.
A) 2,5 B) 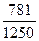 C)
C) 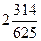 D)
D) 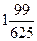 E) 3,5
E) 3,5
19. Егер геометриялық прогрессияның алғашқы алты мүшесінің қосындысы 1820-ға, ал еселігі 3-ке тең болса, бірінші мен бесінші мүшелердің қосындысын табыңыз.
A) 164 B) 246 C) 410 D) 492 E) 328
20. Мүшелері оң геометриялық прогрессияның екінші мүшесі 81, ал үшінші мен төртінші мүшелерінің қосындысы 36-ға тең. Прогрессияның бірінші мен бесінші мүшелерінің айырмасын табыңыз.
A) 216 B) 228 C) 240 D) 204 E) 252
Прогрессия 2
1. Геометриялық прогрессияның алғашқы сегіз мүшесінің қосындысын табыңыз, оның b1 = 512;
q = 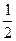 белгілі болса.
белгілі болса.
A) 976 B) 1438 C) 1020 D) 1012 E) 1110
2. Арифметикалық прогрессияның а5 = 8,7 және а8 =12,3 белгілі. d және а1 табыңыз.
A) d = 3,6; а1 = -5,7 B) d = 1,2; а1 = 3,9
C) d = 1,6; а1 = 2,3 D) d = 1,2; а1 = 3,1
E) d = 1,4; а1 = 3,1
3. Арифметикалық прогрессияның төртінші мен алтыншы мүшелерінің қосындысы 14-ке тең. Осы прогрессияның алғашқы тоғыз мүшесінің қосындысын табыңыз.
A) 14 B) 56 C) 64 D) 63 E) 126
4. Арифметикалық прогрессияның алғашқы сегіз мүшесінің қосындысы 120-ға, ал 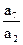 = 5 тең. Прогрессияның бірінші мүшесі және айырмасын табыңыз.
= 5 тең. Прогрессияның бірінші мүшесі және айырмасын табыңыз.
A) а1 = 2; d = 4 B) а1 = 1; d = 5 C) а1 = 1; d = 4
D) а1 = 1; d = 3 E) а1 = 2; d = 3
5. a1 = 10, d = 4, n = 11 болатын арифметикалық прогрессияның соңғы мүшесін есептеңіз.
A) 47 B) 104 C) 43 D) 50 E) 40
6. Егер а7 = 21; а9 = 29 болса, онда арифметикалық прогрессияның бірінші мүшесін және айырмасын табыңыз.
A) а1=13; d = 2 B) а1= -3; d = 4 C) а1=4; d = 3 D) а1=5; d = 3 E) а1=3; d = 4
7. Геометриялық прогрессияның алғашқы он екі мүшесінің көбейтіндісін осы прогрессияның бірінші мүшесінің он бірінші дәрежесіне бөлгенде шығатыны ...
A) Прогрессияның он бірінші мүшесі
B) Прогрессияның алпыс сегізінші мүшесі
C) Прогрессияның алпыс жетінші мүшесі
D) Прогрессияның алпыс алтыншы мүшесі
E) Прогрессияның он екінші мүшесі
8. Арифметикалық прогрессияның үшінші мен бесінші мүшелерінің қосындысы 22-ке тең. Осы прогрессияның алғашқы жеті мүшесінің қосындысын табыңыз.
A) 88 B) 66 C) 64 D) 77 E) 76
9. 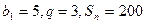 болатын шектеулі геометриялық прогрессияның мүшелерінің саның табыңыз.
болатын шектеулі геометриялық прогрессияның мүшелерінің саның табыңыз.
A) 5 B) 6 C) 3 D) 4 E) 2
10. Алғашқы жүз жұп натурал сандардың қосындысын табыңыз.
A) 2550 B) 10100 C) 10302 D) 9898 E) 9999
11. Арифметикалық прогрессияның екінші мүшесі 9-ға, ал үшінші мүшесі бірінші мүшесінен 12-ге артық. Алғашқы он мүшесінің қосындысын табыңыз.
A) 310 B) 290 C) 300 D) 320 E) 280
12. Арифметикалық прогрессияның 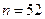 ;
; 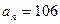 ;
; 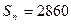 екендігі белгілі. Прогрессияның бірінші мүшксін мен айырмасын табыңыз.
екендігі белгілі. Прогрессияның бірінші мүшксін мен айырмасын табыңыз.
A) 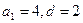 B)
B) 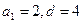 C)
C) 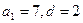
D) 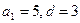 E)
E) 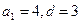
13. Геометриялық прогрессияда 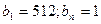 ;
; 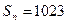 . Мүшелерінің саны мен еселігін табыңыз.
. Мүшелерінің саны мен еселігін табыңыз.
A) 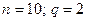 B)
B) 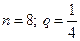 C)
C) 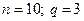
D) 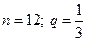 E)
E) 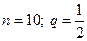
14. Геометриялық прогрессияның бірінші мүшесі 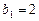 , ал оның еселігі
, ал оның еселігі 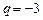 . Осы прогрессияның алғашқы бес мүшелерінің қосындысын табыңыз.
. Осы прогрессияның алғашқы бес мүшелерінің қосындысын табыңыз.
А) 324 В) 184 С) 160 D) 122 Е) 132
15. Арифметикалық прогрессияның 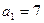 ,
, 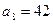 екендігі белгілі. Осы прогрессияның алғашқы алты мүшесінің қосындысын табыңыз.
екендігі белгілі. Осы прогрессияның алғашқы алты мүшесінің қосындысын табыңыз.
A) 102 B) 117 C) 125 D) 118 E) 116
16. Арифметикалық прогрессиянын алғашқы он бес мүшелерінін қосындысы 225-ке,ал екінші мүшесі 3-ке тен.Осы прогрессиянын үшінші мен бесінші мүшелерінін қосындысы н табыныз.
A) 20 B) 18 C) 12 D) 16 E) 14
17. Геометриялық прогрессияның төртінші мүшесінің оның бірінші мүшесіне бөлгендегі шыққан бөліндісі 64-ке тең, ал прогрессияның үшінші мүшесі 8-ге тең. Бірінші мүшесін табыңыз.
A) 1 B) 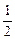 C) 4 D)
C) 4 D) 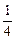 E) 2
E) 2
18. Мүшелері оң өспелі геометриялық прогрессияның бірінші және төртінші мүшелерінің көбейтіндісі 27, ал екінші мен үшінші мүшелерінің қосындысы 12 тең. Екінші мен бесінші мүшелерінің қосындысын табыңыз.
A) 85 B) 83 C) 82 D) 86 E) 84
19. 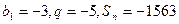 болатын шектеулі геометриялық прогрессияның мүшелерінің саның табыңыз.
болатын шектеулі геометриялық прогрессияның мүшелерінің саның табыңыз.
A) 5 B) 6 C) 3 D) 4 E) 2
20. Геометриялық прогрессияның еселігі 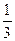 , төртінші мүшесі
, төртінші мүшесі 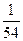 -ге, барлық мүшелерінің қосындысы
-ге, барлық мүшелерінің қосындысы 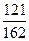 -ге тең болса, онда прогрессияның мүшелерінің саның табыңыз.
-ге тең болса, онда прогрессияның мүшелерінің саның табыңыз.
A) 2 B) 5 C) 7 D) 3 E) 4
