Погрешности квантования

В метрологической практике широкое распространение получили цифровые СИТ, т.е. такие измерительные приборы и ИП, в которых по принципу действия осуществляется квантование измеряемой величины по уровню. В процессе квантования происходит измерительное преобразование непрерывно изменяющейся величины 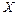в ступенчато изменяющуюся величину с заданными размерами ступеней (рис. 4.8). При этом бесконечному множеству возможных значений величин 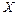ставится в соответствие конечное и счетное множество возможных показаний или выходных кодов цифрового устройства .

Квантованию, как измерительному преобразованию, присуща методическая погрешность, возникающая при отображении непрерывной по размеру величины 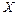ограниченным по числу разрядов числом . Погрешность квантования равна разности между результатами измерения и истинным значением величины 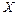(рис. 4.8)

, (4.29)

если погрешность меры и компаратора равны нулю. Таким образом, как следует из (4.29), зависимость погрешности квантования 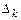от измеряемой величины 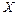линейна в пределах шага квантования .

В цифровых СИТ измеряемая величина 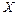, находящаяся между двумя уровнями квантования и , как правило, отражена нижним числовым значением . В этом случае погрешность квантования 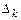всегда отрицательна, а ее максимальное (по модулю) значение равно шагу квантования (рис.4.8).

Погрешность квантования 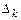по характеру изменения может быть систематической постоянной по значению (при ) и случайной (при по случайному закону). В последнем случае закон изменения 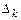аналогичен закону изменения измеряемой величины 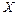. При равномерном законе изменения величины 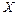погрешность квантования распределена по равномерному закону с математическим ожиданием ; СКО . Характер изменения погрешности 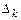предполагает и способы ее уменьшения.

Если измеряемая величина постоянна по размеру, то погрешность 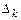также является постоянной величиной и может быть определена с помощью более высокочувствительного прибора или (при отсутствии такового) наложением случайного сигнала с последующей статистической обработкой ряда измерений. Для реализации второго способа на вход цифрового измерительного прибора (ЦИП) необходимо подать дополнительный случайный центрированный сигнал с известным законом распределения . На входе ЦИП образуется суммарный случайный сигнал (рис. 4.9).

При ЦИП при повторных измерениях выдает неизменный результат , содержащий погрешность . Когда , ЦИП выдает различные результаты измерения и т.д. Для определения эти результаты подвергаются статистической обработке.

Обработка может заключаться в определении среднего значения ряда 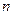измерений , которое будет приближаться к значению 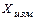с СКО . В этом случае погрешность квантования определяют по формуле

. (4.30)

Однако среднее значение ряда показаний ЦИП становится несмещенной оценкой математического ожидания измеряемой величины только при больших по сравнению со ступенью квантования изменениях измеряемой величины (или СКО дополнительного сигнала).

При известном распределении дополнительного случайного сигнала с известным определяют вероятность , соответствующую факту , где 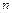- общее число измерений ; - число измерений, при которых было меньше (рис.4.9).

Эта вероятность, очевидно, будет равна

, (4.31)

где - значение интегральной функции распределения дополнительного сигнала в точке .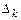

Таким образом, имея аналитическое выражение для интегральной функции распределения дополнительного сигнала , можно для определить значение .

Так для равномерного закона с предельным отклонением , аналитическое выражение для определения погрешности квантования будет иметь вид

. (4.32)

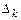В случае нормального закона распределения с известным среднеквадратическим отклонением погрешность определяется по формуле

, (4.33)

где - аргумент нормированного нормального распределения при .

На практике удобно формировать дополнительный входной сигнал в виде синусоидально - изменяющегося воздействия с известным значением среднеквадратического отклонения . В этом случае погрешность 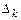можно определить по формуле

. (4.34)

Погрешность определения 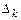статистическим способом, зависит от количества измерений и отношения к шагу квантования . Определив значение погрешности квантования 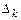, можно уточнить результат измерения, введя в него поправку, по формуле

, (4.35)

вытекающей из выражения (4.29).