Лекция №5. Кирхгоф заңдары. Кирхгофтың заңдарын қолдану. Суперпозиция әдісі. Түйіндік кернеу әдісі. Контурлы токтар әдісі

3.1. Кирхгофтың заңдарын қолдану

Кирхгофтың заңдары көмегімен электрлік тізбекті есептеу үшін

1) тізбекте тоқ бағытын еркімізше таңдау керек;

2) Кирхгофтың І – заңына сәйкес тізбектегі түйін санынан бірге кем болатын теңдеулер құру қажет;

3) Кирхгофтың ІІ – заңы бойынша есепті шешуге қажетті теңдеулерді жазу керек. Контурды таңдаған кезде алдында қарастырылмаған тармағын таңдау қажет;

4) Тоқтарды анықтағаннан кейін осы тоқтардың нақты бағытын дәлірек анықтау керек.

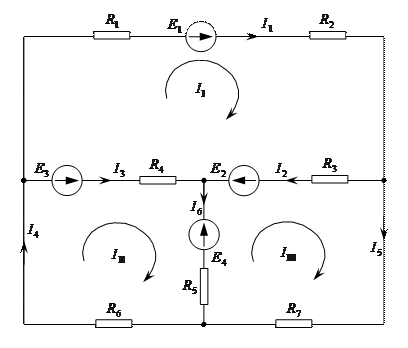
Мысалы. 2.5 –суреттегі электр тізбегін есептеу үшін мынадай теңдеулер құруға болады:

;

;

;

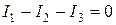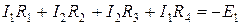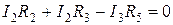3.2. Суперпозиция әдісі

Егер тізбекте бірнеше қоректендіру көзі бар болса, онда мұндай тізбекті есептеу үшін суперпозиция әдісін қолдануға болады. Бұл әдіс ЭҚК әсерлерінің тәуелсіздік принципін пайдаланады. Бірнеше ЭҚК тудыратын тоқтар жеке әрбір тоқ көзі тудырған тоқтардың алгебралық қосындысы болып табылады. Суперпозиция әдісі күрделі тізбектерді есептеуді әрқайсысында бір тоқ көзі бар элементар тізбектерді есептеумен алмастыруға мүмкіндік береді.

Бірнеше қоректендіру көзі бар күрделі тізбектерді есептеуді суперпозиция әдісі бойынша төмендегідей жасауға болады:

1) күрделі тізбекті әрбір элементар тізбекте бір тоқ көзі болатындай бірнеше тізбекпен ауыстырады, басқалары тоқ көзінің ішкі кедергілеріне тең кедергілермен ауыстырылады;

2) әрбір тармақтағы тоқтардың шамалары мен бағыттарын анықтай отырып, элементар тізбектерді есептейді;

3) әрбір тармақтағы сәйкес тоқтардың алгебралық қосындысы ретінде нақты тоқтарды табады, яғни нақты тоқтардың қосындылары элементар тізбектердегі осы тармақтың тоқтары болып табылады.

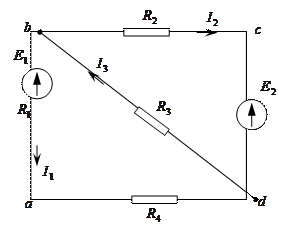Мысалға 3.1 – суретте көрсетілген тізбекті есептейік. Бірінші жағдайда тізбекті 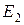ЭҚК-сіз есептейік. Бұл ЭҚК – тің ішкі кедергісі нөлге тең. Барлық тоқтарды штрихпен белгілейік, яғни

;

;

.

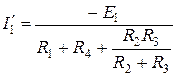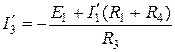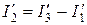3.1 – сурет

Әрі қарай тізбекті 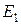тоқ көзісіз қарастыруға болады, бірақ оның 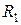ішкі кедергісін ескеру қажет. Тоқтарды екі штрихпен белгілейміз:

;

;

.

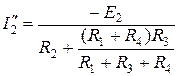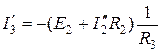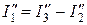Нақты тоқтар элементар тізбектердегі сәйкес тоқтардың қосындысы болып табылады, яғни:

,

,

.

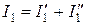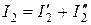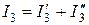3.3. Түйіндік кернеу әдісі

Егер электр тізбегі тек екі түйіннен тұратын болса, онда оны түйіндік кернеу әдісімен есептеген ыңғайлы. 3.2 – суретте 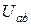кернеуі 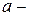дан 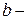ға бағытталған. Әрбір 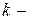шы контурға Кирхгофтың ІІ – заңы бойынша теңдеу мына түрде болады

.

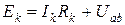Бұл жағдайдағы тізбектің әрбір тармағындағы тоқ

,

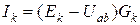мұндағы .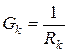

Егер Кирхгофтың І – заңы бойынша теңдеу құрсақ,

,

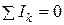яғни ,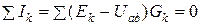

онда түйіндік кернеуді анықтауға болады

.

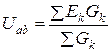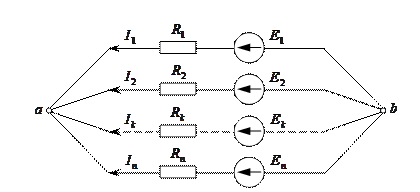
3.2 – сурет

Түйіндік кернеу әдісімен тізбекті есептеу үшін

1) тізбектегі тоқ бағытын еркімізше таңдау қажет;

2) 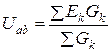түйіндік кернеуді анықтау керек; алымындағы көбейтінді ЭҚК бағыты түйіндік кернеу бағытымен сәйкес келмесе «+» таңбамен алынады;

3) Түйіндік кернеуді анықтағаннан кейін электр тізбегінің барлық тармақтарындағы тоқтарды 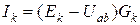бойынша табуға болады.

Егер тоқ теріс мәнге ие болса, онда нақты бағыты схемада белгіленгенге қарама-қарсы болады.

3.4. Контурлы токтар әдісі

Кирхгоф заңдарының көмегімен кез келген электрлік тізбекті есептеуге мүмкіндік бар. Бірақ күрделі тармақталған тізбектер жағдайында өте қолайсыз үлкен теңдеулер жүйесін есептеу қажет. Есептеулерді контурлы тоқтар әдісі жеңілдетеді.

Әдістің мәнісі мынада:

Жалған, шартты (есептейтін) контурлы тоқтар туралы түсінік енгізіледі және ол тек өзінің көршілес контурлық тоқтарымен тұйықталған;

Контурлы тоқтар тармақтағы нақты тоқпен байланысады (аналитикалық түрде);

Контурлы тоқтар үшін Кирхгофтың ІІ – заңы бойынша теңдеулер жүйесі құрылады; нақты тоқтардан контурлы тоқтардың саны едәуір аз, сондай-ақ жүйедегі теңдеулер саны да азаяды;

Теңдеулер жүйесі шешіліп, контурлы тоқтар анықталады;

Аналитикалық тәуелділіктер көмегімен нақты тоқтар анықталады.

Мысалы: 3.3 – сурет

а) көршілес контурлар бойынша схеманы бөлеміз және контурлы тоқтардың ( 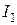, , 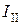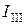) бағыттарын анықтаймыз;

б) контурлы және нақты тоқтардың арасындағы байланысты табамыз

, , ,

, , ;

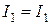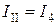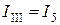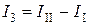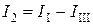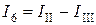в) әрбір контур үшін Кирхгофтың ІІ – заңы бойынша теңдеулер жүйесі құрыламыз:

(1-ші контур) ,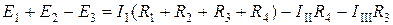

(2-ші контур) ,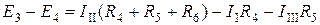

(3-ші контур) ;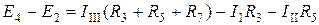

г) жүйені шешіп, контурлы тоқтарды табамыз және тармақтардағы нақты тоқтарды анықтаймыз.