Определение матрицы перехода и её свойства
Определение матрицы перехода
Пусть в линейном пространстве 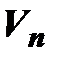 заданы два базиса:
заданы два базиса:
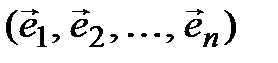 (3.41)
(3.41)
и
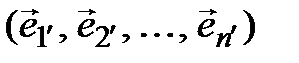 . (3.42)
. (3.42)
Принадлежность вектора второму базису отмечается штрихом, причем удобно штрих ставить не на вектор, а на индекс, например, 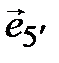 – пятый вектор второго базиса. Тогда каждый из векторов второго базиса можно разложить по первому. Все координаты будем обозначать одной и той же ключевой буквой t с двумя индексами: нижним индексом обозначим номер разлагаемого вектора, а верхним – номер координаты. Таким образом,
– пятый вектор второго базиса. Тогда каждый из векторов второго базиса можно разложить по первому. Все координаты будем обозначать одной и той же ключевой буквой t с двумя индексами: нижним индексом обозначим номер разлагаемого вектора, а верхним – номер координаты. Таким образом,
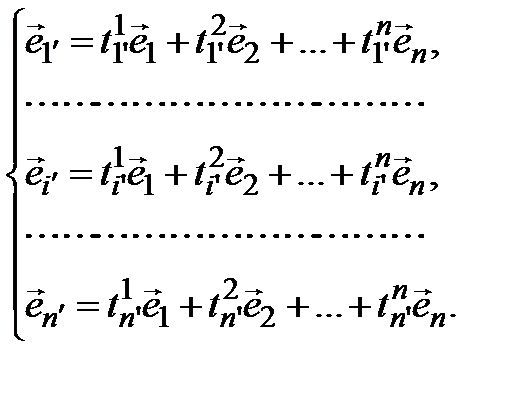 (3.43)
(3.43)
Учитывая нашу договоренность, систему равенств (3.43) можно сокращенно записать одним равенством:
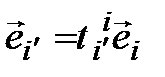 (3.44)
(3.44)
(оцените красоту записи!)
Введем следующие обозначения:
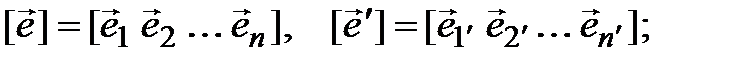
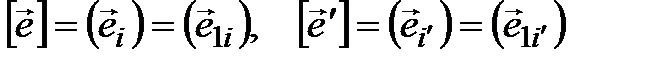
(подчеркиваем, что это матрицы-строки)
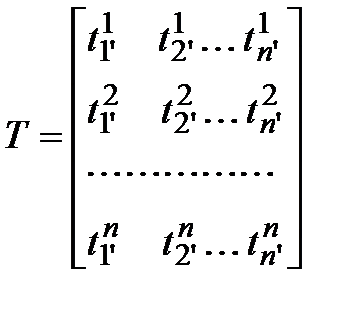 .
.
Тогда 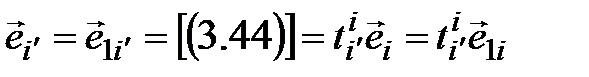 =[располагаем по правилу цепочки] =
=[располагаем по правилу цепочки] = 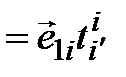 , откуда вытекает, что
, откуда вытекает, что
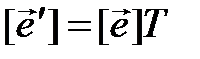 . (3.45)
. (3.45)
Матрицей перехода от базиса (3.41) к базису (3.42) называется матрица Т = 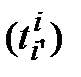 , столбцами которой являются координатные столбцы векторов второго базиса в первом базисе, т. е. матрица, удовлетворяющая системе равенств (3.43) или (3.44), либо одному матричному равенству (3.45).
, столбцами которой являются координатные столбцы векторов второго базиса в первом базисе, т. е. матрица, удовлетворяющая системе равенств (3.43) или (3.44), либо одному матричному равенству (3.45).
Свойства матрицы перехода:
1º. Матрица перехода от одного базиса к другому определяется однозначно.
►Вытекает из того, что она состоит из координатных столбцов векторов одного базиса в другом.◄
2º. Матрица перехода всегда невырождена.
►На основании матричного критерия линейной независимости.◄
3º. Если Т – невырожденная квадратная матрица n-го порядка и
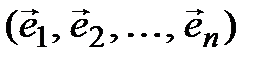 – (3.46)
– (3.46)
некоторый базис пространства 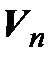 , то в
, то в 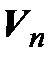 существует базис
существует базис
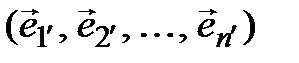 (3.47)
(3.47)
такой, что Т – матрица перехода от (3.46) к (3.47).
►Пусть 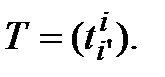 Положим
Положим 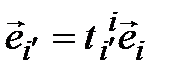 (т. е.
(т. е. 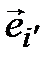 – вектор, чей координатный столбец в базисе (3.46) совпадает с i-м столбцом матрицы Т). Тогда (3.47) – линейно независимая система на основании матричного критерия, а значит, в
– вектор, чей координатный столбец в базисе (3.46) совпадает с i-м столбцом матрицы Т). Тогда (3.47) – линейно независимая система на основании матричного критерия, а значит, в 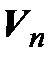 является базисом. Из определения матрицы перехода вытекает, что Т – матрица перехода от (3.46) к (3.47).◄
является базисом. Из определения матрицы перехода вытекает, что Т – матрица перехода от (3.46) к (3.47).◄
4º. Матрица перехода от базиса 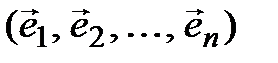 к нему самому является единичной.
к нему самому является единичной.
►Доказательство вытекает из равенства 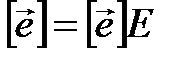 .◄
.◄
5º. Если Т – матрица перехода от базиса (3.46) к базису (3.47),а  - матрица перехода от (3.47) к базису
- матрица перехода от (3.47) к базису
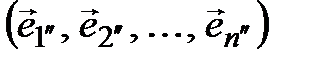 , (3.48)
, (3.48)
то матрицей перехода от (3.46) к (3.48) является матрица 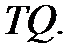
►Действительно, 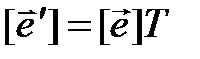 ,
, 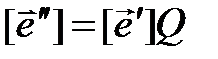 , и поэтому
, и поэтому 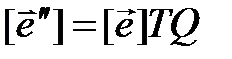 . Утверждение вытекает из определения матрицы перехода.◄
. Утверждение вытекает из определения матрицы перехода.◄
6º. Если Т – матрица перехода от (3.46) к (3.47), то матрицей перехода от (3.47) к (3.46) является 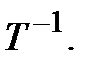
►(3.45) 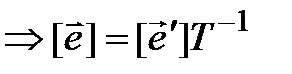 , и утверждение опять вытекает из определения матрицы перехода.◄
, и утверждение опять вытекает из определения матрицы перехода.◄
Замечание. По аналогии с равенством (3.44) естественно записать равенство 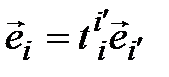 , и поэтому элементы матрицы перехода от (3.47) к (3.46) естественно обозначать
, и поэтому элементы матрицы перехода от (3.47) к (3.46) естественно обозначать 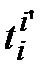 . Учитывая, что эта матрица есть не что иное, как
. Учитывая, что эта матрица есть не что иное, как 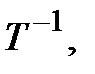 получаем:
получаем: 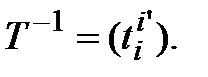 Так как
Так как 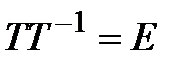 и
и 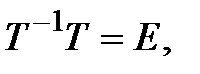 то
то 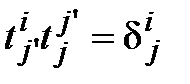 и
и 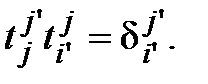
Вопрос 14
