Модель и идентификация объекта управления
А.Ю. ПОПОВСКИЙ
СИНТЕЗ РЕГУЛЯТОРОВ
ЛИНЕЙНЫХ СИСТЕМ
Учебное пособие
Одесса – 2006
ББК 39.42-05
П58
УДК 662-551
Поповский А.Ю.
П58 Синтез регуляторов линейных систем [Текст]: учебное пособие; под общ. ред. С.И. Горба. – Одесса: ОНМА, 2006. – 51 с.
Рецензенты: профессор кафедры высшей математики ОНМА А.Ф. Бурденко, к ф.-м. н.; доцент кафедры "Компьютеризованные системы управления" ОНПУ Бобриков С.А., к.т.н.
Рассмотрены вопросы идентификации объекта управления по его разгонной характеристике, параметрического синтеза регулятора и анализа характеристик замкнутой системы автоматического регулирования.
Приведены расчеты регуляторов с использованием современных программных средств (пакетов MathCAD и MATLAB – SIMULINK).
Пособие предназначено для подготовки курсантов и студентов по направлению 0925 «Автоматизация и компьютерно-интегрированные системы», а также может быть использовано курсантами и студентами других направлений при изучении дисциплин и выполнении курсовых работ и проектов и дипломных проектов, тематика которых включает вопросы моделирования процессов и систем.
| Утверждено ученым советом ОНМА в качестве учебного пособия по направлению 0925 «Автоматизация и компьютерно-интегриро-ванные системы» 31 августа 2006 г., протокол № 1 |
© А.Ю Поповский, 2006.
ВВЕДЕНИЕ
Современные системы управления сложными технологическими объектами строятся по иерархическому принципу, т.е. система управления расчленяется на ряд систем, стоящих на разных уровнях подчинения. Система более высокого ранга, ориентируясь на общий (глобальный) критерий, выдает команды на включение или отключение отдельных локальных объектов и осуществляет выбор частных критериев управления. Локальные системы управления поддерживают заданные оптимальные режимы, как в пусковых, так и в нормальных эксплуатационных условиях.
Являясь нижним иерархическим уровнем автоматических систем управления технологическими объектами, локальные системы осуществляют функции измерения, контроля и регулирования основных технологических параметров, являясь обязательной частью системы управления любым технологическим агрегатом (объектом управления – ОУ).
ОУ обычно является неизменной частью, а регулятор – варьируемой частью системы. Это означает, что структуру и настроечные параметры регулятора можно изменять для создания системы автоматического регулирования (САР) с показателями качества, удовлетворяющими технологическим условиям. Расчет настроечных параметров регулятора и, при необходимости, дополнительных корректирующих звеньев, изменяющих его структуру, является важнейшей составной частью процесса создания (синтеза) систем автоматического управления.
Практика построения систем управления технологическими объектами свидетельствует о широком использовании в промышленных САР типовых линейных алгоритмов регулирования – пропорционального (П), пропорционально-интегрального (ПИ), пропорционально-интегро-дифференциального (ПИД). Промышленные автоматические регуляторы реализуют типовые алгоритмы приближенно, но обычно настройки регулятора рассчитываются без учета отклонения алгоритма от идеального типового, поскольку предполагается, что эти отклонения не оказывают существенного влияния на динамику системы.
Основной задачей корректной настройки системы автоматического регулирования является параметрический синтез регулятора, т.е. определение его оптимальных настроечных параметров.
В настоящем учебном пособии рассмотрены вопросы качества работы линейных систем автоматики с запаздыванием, приводится анализ чувствительности систем и параметрический синтез их регуляторов.
В пособии рассмотрены вопросы по разделам программы учебной дисциплины «Теория автоматического управления»: «Качество систем регулирования»; «Анализ и синтез САУ»; «Коррекция САУ».
МОДЕЛЬ И ИДЕНТИФИКАЦИЯ ОБЪЕКТА УПРАВЛЕНИЯ
Системы управления работой технологических объектов в общем случае относятся к классу инерционных, нелинейных и нестационарных систем, обладающих распределенным характером емкостей. Поэтому динамика их должна описываться нелинейными уравнениями в частных производных с переменными коэффициентами.
Большинство систем регулирования относится к классу однорежимных систем (систем автоматической стабилизации работы объекта относительно его номинального режима). Поэтому, справедливо предположение, что отклонения значений переменных величин (относительно рабочей точки) в процессе работы будут малы. Это, свою очередь, позволяет использовать для описания линейные модели объекта управления. Допустимое, во многих случаях, пренебрежение распределенным характером емкостей позволяет использовать для описания обыкновенные дифференциальные уравнения. Учитывая, что характерное время переходных процессов обычно существенно меньше времени изменения характеристик объекта, обусловленного его нестационарностью, коэффициенты используемых дифференциальных уравнений можно считать постоянными. Математическим выражением такой модели является передаточная функция, записанная в дробно-рациональной форме
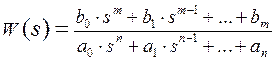 , , | (1) |
где значения коэффициентов 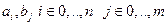 определяются характером процессов в принятой модели описания объекта.
определяются характером процессов в принятой модели описания объекта.
Эти коэффициенты однозначно определяют временные и частотные свойства объекта. В случае нейтрального объекта передаточная функция имеет нулевые полюса (нулевые корни характеристического уравнения), которые отсутствуют в случае устойчивого объекта (объекта с положительным самовыравниванием).
Физическая реальность процессов, протекающих в объекте управления, обуславливает необходимость учета транспортного запаздывания, поскольку часто после нанесения возмущения до начала изменения показателей процесса проходит некоторое время[1]. Это учитывается введением в модель последовательно соединенного звена идеального транспортного запаздывания, поэтому выражение (1) в общем случае должно быть заменено соотношением
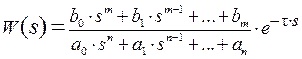 . . | (2) |
На первом этапе задачи синтеза регулятора необходимо провести идентификацию объекта управления , что означает установить конкретный вид передаточной функции (2) и найти численные значения ее коэффициентов.
Одному и тому же объекту можно сопоставить множество различных по сложности моделей, каждая из которых будет нести достаточную информацию о свойствах объекта с позиций конкретно поставленной задачи. Обычно предварительные соображения о предполагаемой структуре и алгоритмах функционирования САР позволяют упростить форму модели, и, не отображая скрупулезно все особенности, выделить более важные стороны динамики объекта, пренебрегая несущественными.
Существуют аналитические и экспериментальные методы получения математического описания объектов управления. Аналитические методы базируются на использовании уравнений, описывающих физико-химические и энергетические процессы, протекающие в исследуемом объекте управления. Это, например, законы сохранения вещества и энергии (уравнения материального баланса). В настоящее время для многих классов объектов управления – теплоэнергетические объекты (ядерные реакторы, паровые турбины, генераторы, двигатели), технологические объекты (химические реакторы), аэрокосмические объекты (ракеты, самолеты, вертолеты) – получены их математические модели.
Хотя знание закономерностей процессов, протекающих внутри объекта управления, и позволяет определить вид дифференциального уравнения, описывающего его динамику, однако нахождение коэффициентов уравнения по конструктивным данным объекта обычно достаточно сложно. Значительно проще представляется провести серию экспериментов на реальном объекте управления и обработать, соответствующим образом, их результаты.
Под обработкой понимают замену ввода в память компьютера непосредственно полученных данных оценкой параметров динамической модели на основе предварительного задания ее структуры, т.е. нахождение аналитической аппроксимации экспериментальных результатов функцией, основанной на конкретном выражении (2).
Экспериментальные методы определения динамических характеристик объектов управления делятся на активные и пассивные.
Активные методы предполагает подачу на вход объекта пробных тестирующих сигналов, с последующей обработкой реакции на них. Эти сигналы могут быть регулярными функциями времени (ступенчатый или прямоугольный импульсы, гармонический сигнал, периодический двоичный сигнал); или же входные сигналы могут носить случайный характер (белый шум, псевдослучайный двоичный сигнал). Хотя активные методы обеспечивают высокую точность получения математического описания и относительно малую длительность эксперимента, но одновременно они, в той или иной степени, приводят к нарушению нормального хода технологического процесса. Поэтому проведение активных экспериментов следует тщательно планировать. В пассивных методах на вход объекта не подаются никакие пробные сигналы, а лишь фиксируется естественное движение объекта в процессе его нормального функционирования. Полученные реализации массивов данных входных и выходных сигналов обрабатываются статистическими методами, что позволяет получить параметры передаточной функции объекта. Недостатками этих методов являются малая точность получаемого математического описания (т.к. отклонения от нормального режима работы малы) и необходимость накопления больших массивов данных с целью повышения точности (тысячи точек) а также, если эксперимент проводится на объекте, охваченном системой регулирования, то учет эффекта корреляции входного и выходного сигнала.
В соответствии с характером воздействия на объект управления экспериментальные методы делятся на частотные и методы переходных процессов.
Для определения частотных характеристик исследуется установившийся режим вынужденных колебаний объекта. При этом предполагается, что эти колебания вызваны подачей на вход объекта периодического сигнала[2] с известной частотой и амплитудой. Далее производится последующий сравнительный анализ графиков входного и выходного сигналов либо их синхронное детектирование. Наличие нелинейности статической характеристики объекта можно установить анализируя степень ангармоничности выходного сигнала. Предварительно (обычно, методом двухпозиционного регулирования неполным притоком) находят критическую частоту колебаний объекта ωπ, т.е. частоту, на которой входная и выходная гармоники колеблются в противофазе. Она в соотношении 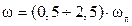 задает рабочий диапазон частот эксперимента (обычно 6¸7 точек). Определяемая амплитудно-фазовая характеристика объекта несет большую информации, чем кривая разгона, и позволяет получить более точную динамическую модель, работающую в широком диапазоне частот. Далее выбирают нужный вид передаточной функции и определяют такие значения ее параметров, чтобы АФХ модели как можно точнее соответствовала АФХ реального объекта. Недостатками частотных методов является их большая трудоемкость и необходимость использования специальной аппаратуры (низкочастотные генераторы периодических сигналов и регистрирующая аппаратура, пригодная для работы на больших объектах).
задает рабочий диапазон частот эксперимента (обычно 6¸7 точек). Определяемая амплитудно-фазовая характеристика объекта несет большую информации, чем кривая разгона, и позволяет получить более точную динамическую модель, работающую в широком диапазоне частот. Далее выбирают нужный вид передаточной функции и определяют такие значения ее параметров, чтобы АФХ модели как можно точнее соответствовала АФХ реального объекта. Недостатками частотных методов является их большая трудоемкость и необходимость использования специальной аппаратуры (низкочастотные генераторы периодических сигналов и регистрирующая аппаратура, пригодная для работы на больших объектах).
Для определения временных характеристик анализируются характер релаксационных процессов в объекте управления, вызванных изменением входного воздействия. Одним из основных используемых на практике методов идентификации объекта является метод исследования реакции объекта на входное воздействие в виде ступенчатого сигнала. В этом случае выходной сигнал представляет собой разгонную характеристику. Если же на вход подается прямоугольный импульс, то фиксируется кривая отклика, которая должна быть достроена до соответствующей кривой разгона. Кривую разгона желательно снимать:
- в окрестности рабочей точки процесса;
- как при положительных, так и отрицательных скачках управляющего сигнала, что позволяет судить об асимметрии, наиболее часто проявляющейся в тепловых ОУ);
- несколько раз, с последующим наложением, с целью исключения эффекта зашумленности выхода;
- на наиболее стабильных режимах процесса, когда действие внешних случайных возмущений маловероятно;
- так, чтобы амплитуда тестирующего входного сигнала была, с одной стороны, достаточно большой, чтобы кривая разгона четко выделялась на фоне шумов, и, с другой стороны, достаточно малой, чтобы не нарушать нормального хода технологического процесса.
Предварительное определение вида передаточной функции, соответствующей выбираемой модели объекта, может быть сделано по внешнему виду разгонной характеристики. Чаще всего тестируемые объекты управления являются устойчивыми (обладают положительным самовыравниванием) и в переходном процессе отсутствует колебательность, что означает отсутствие нулей передаточной функции и чисто вещественный характер ее полюсов.
Устойчивость объекта означает, что значение коэффициента усиления может быть найдено по асимптотическому поведению разгонной характеристики. Если доминирующее воздействие на динамику объекта оказывает только одна емкость и эффектом запаздывания можно пренебречь, то переходная характеристика описывается экспоненциальной зависимостью и объект можно представить апериодическим звеном первого порядка с передаточной функцией
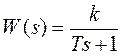 , , | (3) |
где параметры k (коэффициент усиления) и Т (время разгона) легко могут быть найдены графически (рис. 1, а). С другой стороны время разгона объекта можно определить, если провести процедуру интерполяции заданной в узлах функции разгонной характеристики и определить – в какой момент времени выходная величина достигает значения 63 % от установившегося уровня.
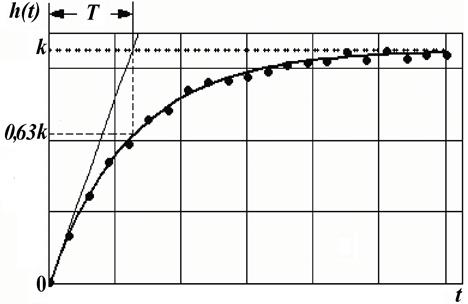 а а |
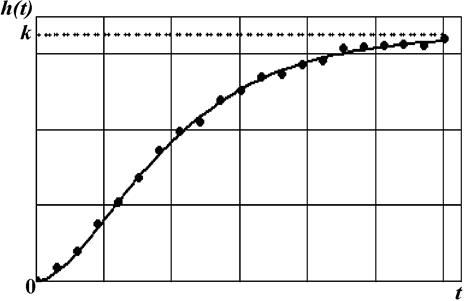 б б |
| Рис. 1. Аппроксимация экспериментально определенных значений разгонной характеристики устойчивого объекта на основании выбранной модели: а - одноемкостный объект, б – многоемкостный объект с малым транспортным запаздыванием |
Если устойчивый объект содержит в своем составе несколько емкостей, а эффектом транспортного запаздывания можно, по-прежнему, пренебречь, то разгонная характеристика его имеет характерную S-образную форму, т.е. содержит точку перегиба (рис. 1, б). В этом случае объект описывается дифференциальным уравнением выше второго порядка, а передаточная функция, соответствующая выбираемой модели представляется, в простейшем случае, выражением вида
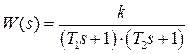 . . | (4) |
Процедура определения двух постоянных времени 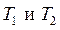 в формуле (4) включает в себя нахождение координаты точки перегиба графика и наклона функции в этой точке, с последующим решением системы нелинейных уравнений. Поэтому во многих практических задачах объект условно представляют последовательным соединением апериодического звена первого порядка и звена идеального транспортного запаздывания.
в формуле (4) включает в себя нахождение координаты точки перегиба графика и наклона функции в этой точке, с последующим решением системы нелинейных уравнений. Поэтому во многих практических задачах объект условно представляют последовательным соединением апериодического звена первого порядка и звена идеального транспортного запаздывания.
Такой модели соответствует передаточная функция
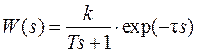 , , |
где τ – время транспорного запаздывания.
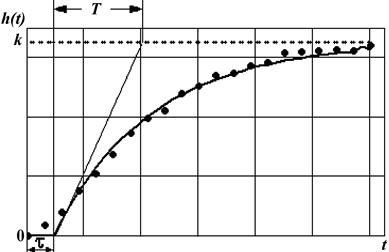 Рис. 2. Аппроксимация экспериментально определенных значений разгонной характеристики устойчивого многоемкостного объекта введением фиктивного звена транспортного запаздывания Рис. 2. Аппроксимация экспериментально определенных значений разгонной характеристики устойчивого многоемкостного объекта введением фиктивного звена транспортного запаздывания |
Выбранная модель соответствует замене реального динамического запаздывания в объекте, обусловленного его неодноемкостностью, условным транспортным запаздыванием, т.е. представлением разгонной характеристики в виде ломаной зависимости (рис. 2). Теперь по-прежнему легко рассчитать параметры модели графически. Однако легкость подобного подхода уравновешивается тем, что точность его трудно оценить. Он может давать значительную погрешность, особенно на начальном этапе переходного процесса, при этом погрешность возрастает для малого числа точек разгонной характеристики и для объектов с малым коэффициентом самовыравнивания. Кроме того, такой подход в принципе не позволяет идентифицировать объекты, обладающие колебательной разгонной характеристикой.
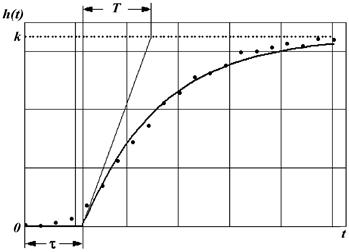
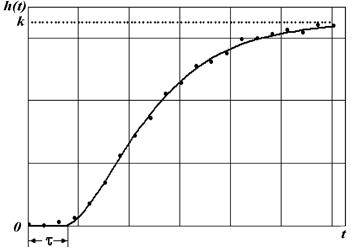
В реальных устойчивых объектах разгонная характеристика чаще всего имеет вид изображенный на рис. 3. Визуальный анализ графика позволяет предположить, что в объекте динамическое запаздывание, обусловленное наличием нескольких емкостей, комбинирует с реально существующим транспортным запаздыванием.
Для проектирования систем регулирования технологических объектов с типовыми регуляторами вполне приемлемым является следующая формула передаточной функции объекта
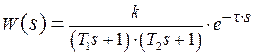 . . | (5) |
Более упрощенной является модель одноемкостного звена с транспортным запаздыванием, описываемая передаточной функцией (4). Это отвечает тому, что комбинация динамического и транспортных запаздываний заменяется одним эффективным транспортным. Такая, более грубая модель, частично отражает основные черты динамики объекта и именно ее параметры обычно используются для расчета настроек регулятора в приближенных инженерных методах расчета.. Результат аппроксимации в рамках моделей (4) и (5) представлен на рис 3. Очевидно, что случай, отвечающий модели с передаточной функцией вида (4), демонстрирует большее несовпадение (невязку) с экспериментом, сравнительно с моделью, отвечающей уравнению (5). Вместе с тем, подобный вид аппроксимации достаточно легко выполнить вручную графически с минимальной, относительно точной процедуры погрешностью.
Расчет параметров передаточной функции модели, т.е. идентификация по разгонной характеристике предполагает необходимость решения обратной задачи Коши – нахождения коэффициентов дифференциального уравнения по известному решению его. Для реализации процедуры поиска параметров модели эффективным представляется метод наименьших квадратов.
 а а |
 б б |
| Рис. 3. Аппроксимация экспериментально определенных значений разгонной характеристики устойчивого объекта: а – модель одноемкостного объекта с транспортным запаздыванием; б – модель многоемкостного объекта с транспортным запаздыванием |
Идея этого метода представляется в следующем:
Вначале выразим переходную функцию модели через ее передаточную функцию с помощью формулы
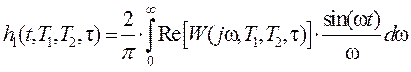 . . | (6) |
Очевидно, что характер переходной функции (форма графика) зависит от выбранных значений параметров модели и нашей задачей является подобрать их так, чтобы добиться наилучшего совпадения аппроксимирующей функции с экспериментальной разгонной характеристикой.
Чем ближе параметры 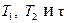 к истинным значениям, тем ближе будет проходить график аппроксимирующей зависимости к заданным значениям. Поэтому сумма расстояний от кривой (6) до точек графика заданной разгонной характеристики может служить оценкой корректности процедуры аппроксимации – чем эта сумма меньше, тем – точнее найдены параметры объекта. Примем эту сумму за целевую функцию задачи и выразим ее аналитически. Для этого аппроксимирующую функцию (6) будем вычислять только в те моменты времени t=ti, когда определена экспериментальная разгонная характеристика
к истинным значениям, тем ближе будет проходить график аппроксимирующей зависимости к заданным значениям. Поэтому сумма расстояний от кривой (6) до точек графика заданной разгонной характеристики может служить оценкой корректности процедуры аппроксимации – чем эта сумма меньше, тем – точнее найдены параметры объекта. Примем эту сумму за целевую функцию задачи и выразим ее аналитически. Для этого аппроксимирующую функцию (6) будем вычислять только в те моменты времени t=ti, когда определена экспериментальная разгонная характеристика 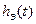 . Целевая функция задачи будет определяться формулой
. Целевая функция задачи будет определяться формулой
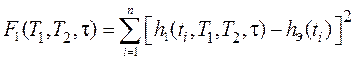 . . | (7) |
Для поиска минимума целевой функции удобно использовать возможности пакетов компьютерной математики. Так, в пакете MathCAD поиск экстремума функции нескольких переменных реализуется с помощью встроенной процедуры Minimize. Для запуска итерационной процедуры необходимо задать начальное приближение – исходные значения искомых параметров.
Заметим, что при вычислении каждого из значений целевой функции в итерационном процессе предусматривается n-кратное вычисление несобственного интеграла. Для ускорения вычислительной процедуры рекомендуется заменить верхний предел интеграла предельной частотой we, для которой подынтегральная функция практически обращается в нуль. Проблемой здесь является то, что это значение заранее неизвестно, т.е. проверить правильность его выбора можно только после проведения процедуры идентификации. Для предварительной оценки этого значения оценки этого значения достаточно оценить визуально эффективное время разгона Т, как это выполнено на рис. 3, а и принять 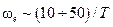 .
.
Для оценки точности идентификации следует:
- Вычислить среднеквадратичное отклонение аппроксимирующей функции от экспериментальной:
 | (8) |
где N – число пар значений заданной разгонной характеристики.
- построить графики экспериментальной и аппроксимирующей зависимости (первый в виде точек, а второй в виде непрерывной линии) и сравнить их поведение.
В заключение следует построить график ВЧХ объекта и оценить верно ли произведена замена верхнего предела интегрирования в несобственном интеграле (6).
Вопросы для самоконтроля
1. Как производится идентификация объекта управления по его временным и частотным характеристикам?
2. В чем заключаются активные и пассивные методы идентификации?
3. Какие Вам известны альтернативные варианты выбора формы передаточной функции устойчивого объекта управления?
4. Как составляется целевая функция метода идентификации и каков алгоритм поиска ее минимума в пакете Mathcad?
5. Как производится проверка точности процедуры идентификации?
