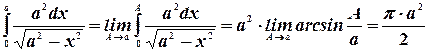Основные свойства определенных интегралов
Определенный интеграл
Оглавление.
1. Понятие определенного интеграла.
2. Основные свойства определенных интегралов.
3. Формула Ньютона-Лейбница.
4. Интегрирование подстановкой.
5. Интегрирование по частям в определенном интеграле.
6. Несобственные интегралы.
7. Вычисление площадей плоских фигур.
8. Вычисление длины дуги плоской кривой.
9. Вычисление объём тела по площади поперечного сечения.
10. Вычисление объем тела вращения.
|
|
|
|
Понятие определенного интеграла
 |
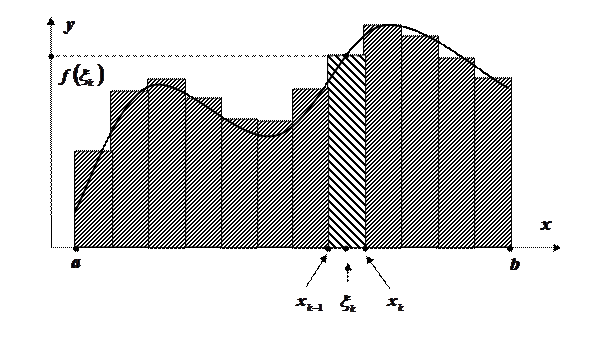Пусть дана функция
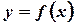, определенная на отрезке 
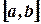. Этот отрезок разобьем на 
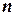элементарных отрезков, шириной 
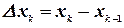, где 
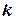- номер отрезка. В каждом из этих элементарных отрезков выберем произвольную точку 
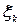. Значение функции в этой точке 
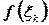умножим на длину отрезка 
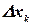, получим произведение 
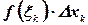. Составим сумму всех таких произведений
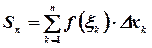
Эта сумма называется интегральной суммой для функции 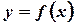на отрезке .
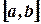Определенным интегралом от функции 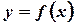на отрезке 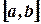называется конечный предел ее интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина их стремится к нулю. Определенный интеграл обозначается символом 
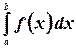(читается: определенный интеграл от 
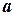до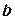 
); 
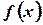называется подынтегральной функцией, 
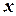- переменной интегрирования, 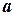- нижним, 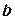- верхним пределом интегрирования.
Следовательно, по определению
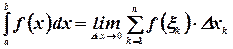
Определенный интеграл численно равен площади криволинейной трапеции, ограниченной кривой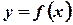 
, прямыми 
, 
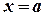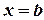и осью 
.
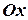Теорема (существования определенного интеграла).
Если функция 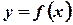непрерывна на 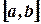, то для нее существует определенный интеграл, т.е. существует предел интегральной суммы, составленный для функции 
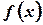на 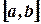, и этот предел не зависит от способа разбиения 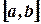на элементарные части и от выбора в них точек 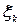, при условии, что 
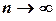и наибольший 
.
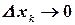Отметим, что определенный интеграл - это число, в то время как неопределенный интеграл - это функция.
Основные свойства определенных интегралов
1. 
.
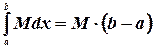2. 
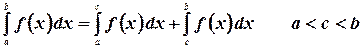- интеграл от конечного числа алгебраической суммы равен алгебраической сумме интегралов.
3. 
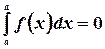- определенный интеграл равен нулю при равенстве верхнего и нижнего пределов.
Замечание. До сих пор мы предполагали, что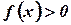 
и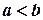 
. Понятие определенного интеграла распространяется и на случай, когда 
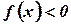и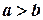 
.
4. 
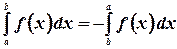- при перемене верхнего и нижнего пределов интеграл меняет знак.
5. 
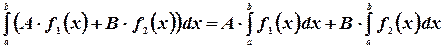-постоянный множитель можно выносить за знак интеграла.
6. 
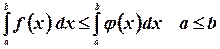если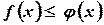 
- неравенство можно почленно интегрировать.
7. 
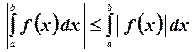- модуль от интеграла меньше или равен интегралу от модуля. Этот пункт отражает известную теорему: Модуль суммы меньше или равен суммы модулей.
Теорема о среднем. Если функция 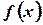интегрируема на отрезке 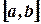и для всех 
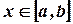выполняется неравенство 
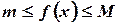, то
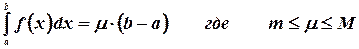
Формула Ньютона-Лейбница
Вычисление определенного интеграла как предела интегральной суммы очень сложно.
Ньютон и Лейбниц доказали теорему, связывающую два важных понятия математического анализа - интеграла и производной. Эта теорема выражается соотношением (формула Ньютона-Лейбница)
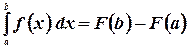
Таким образом, для того чтобы вычислить определенный интеграл от непрерывной функции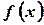 
на отрезке 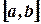, надо узнать ее первообразную функцию 
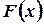и взять разность 
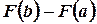значений этой первообразной на концах отрезка .
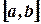Еще раз отметим, что определенный интеграл это число, в то время как неопределенный - это функция. Поэтому совершенно все равно, по какой переменной (букве) ведется интегрирование
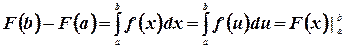
Пример. Вычислить интеграл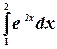 
.
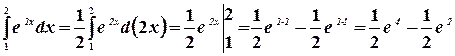
Пример. Вычислить интеграл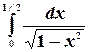 
.
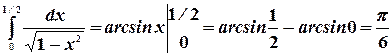
4. Интегрирование подстановкой.
Теорема: Имеет место равенство
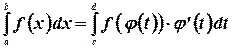
где функция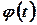 
непрерывно дифференцируема на 
, 
, 
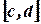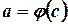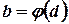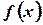и непрерывна на 
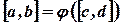- образе отрезка 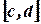при помощи функции 
.
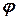Доказательство. Пусть 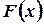и 
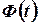- первообразные функции соответственно 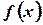и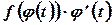 
. Тогда справедливо тождество
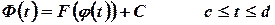
где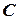 
- некоторая постоянная. Поэтому
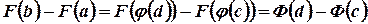
На основании формулы Ньютона-Лейбница, левая часть этого равенства равна левой части равенства теоремы, соответственно и правые части, что доказывает теорему.
Пример. Найти интеграл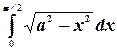 
.
Сделаем замену переменных: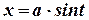 
. Найдем дифференциал : 
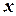. В результате наш интеграл примет вид:
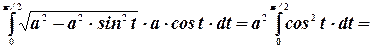
Преобразуем подынтегральное выражение:
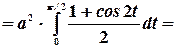
Взяв этот интеграл, получим:
.
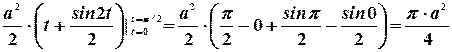5. Интегрирование по частям в определенном интеграле.
Теорема. Справедлива формула интегрирования по частям для определенного интеграла
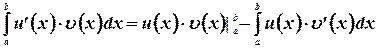
где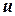 
и 
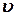- непрерывно дифференцируемые на 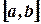функции.
Доказательство. Произведение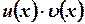 
имеет на 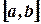непрерывную производную
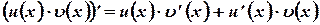
Поэтому по теореме Ньютона-Лейбница
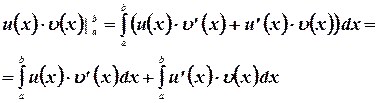
Этим теорема доказана.
Пример.Найти интеграл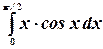 
.
Обозначим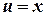 
и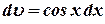 
. Тогда 
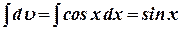. Поэтому
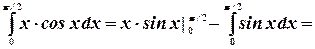
Или, окончательно
.
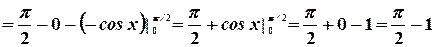Если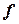 
- четная функция 
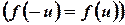, то
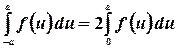
Пример.Найти интеграл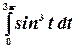 
.
Преобразуем этот интеграл к виду
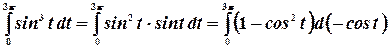
Сделаем замену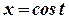 
. В результате пределы интегрирования изменятся: 
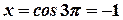и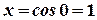 
. В результате получим:
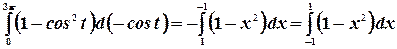
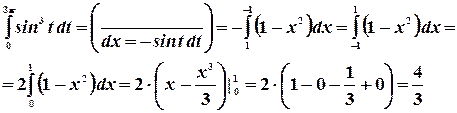
Далее, если 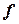- нечетная функция 
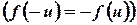, то
.
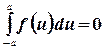Если 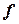- периодическая функция периода 
- 
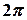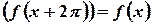, то
.
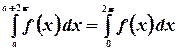Такие особенности в некоторых случаях упрощают процесс интегрирования.
Пример.Вычислить интеграл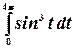 
.
Преобразуем этот интеграл к виду:
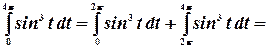
Пределы интегрирования во втором интеграле представим как:
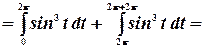
Согласно свойству периодической функции, перепишем это выражение:
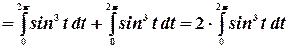
Преобразуем далее
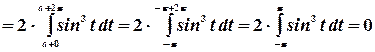
Пример. Определить объем продукции, произведенной рабочим за третий час рабочего дня, если производительность труда характеризуется функцией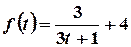 
.
График этой функции имеет вид, изображенный на рисунке.
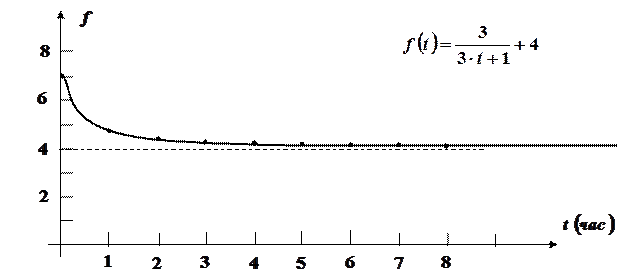
Решение.Если непрерывная функция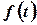 
характеризует производительность труда рабочего в зависимости от времени 
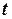, то объем продукции, произведенной рабочим за промежуток времени от 
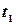до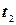 
будет выражаться формулой:
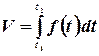
В нашем случае:
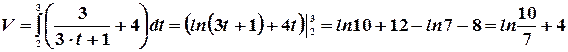
Пример. Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией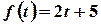 
.
Решение.Имеем:
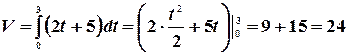
6. Несобственные интегралы.
Пусть на конечном полуинтервале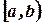 
задана функция 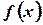такая, что она интегрируема (т.е. конечна) на любом интервале 
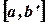, где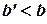 
, но неограниченна в окрестности точки 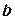. Тогда ее интеграл на 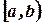, или, что то же самое, на 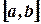не может существовать, так как интегрируемая функция должна быть ограничена.
Однако может случиться так, что существует конечный предел
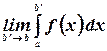
То есть функция не ограничена, а ее интеграл ограничен. В этом случае записанный предел называют несобственным интегралом от 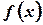на отрезке 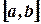и записывают в виде
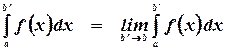
В таком случае говорят, что интеграл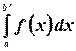 
сходится. В противном случае говорят, что он расходится или не существует как несобственный риманов интеграл.
Аналогично и на полуинтервале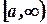 
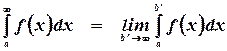
В связи с этим выражение
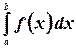
называется интегралом от 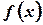с единственной особенностью в точке 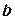, если выполняется следующее условие: если 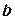конечная точка, то функция 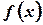интегрируема на 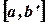при любом 
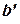удовлетворяющим неравенствам 
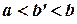, и, кроме того, не ограничена в точке 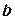. Если же 
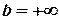, то про функцию 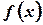предполагается лишь, что она интегрируема на 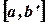при любом конечном 
.
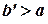Также различают несобственные интегралы первого типа (с одним или двумя бесконечными пределами) и несобственные интегралы второго типа (от разрывных функций).
Несобственный интеграл первого рода, вычисляется обычно как
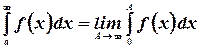
Пример. Найти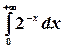 
.
Имеем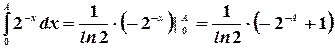 
.
При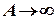 
это выражение имеет предел 
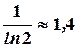. Значит 
.
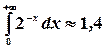Пример. Найти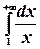 
.
Имеем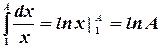 
. Этот интеграл расходится.
Пример. Найти площадь бесконечной полосы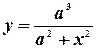 
(верзьера Аньези).
.
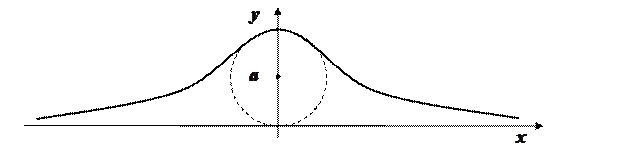
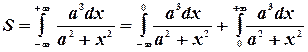Далее, имеем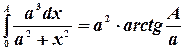 
.
Отсюда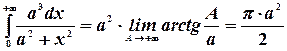 
.
Аналогично вычисляется и первое слагаемое. В итоге получим:
.
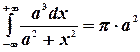Пример. Найти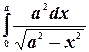 
.
Данный интеграл - несобственный, так как подынтегральная функция терпит разрыв в точке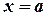 
. Однако этот интеграл сходится, так как
