Лінійні рівняння та ті, що зводяться до них
У 7-му класі проводиться систематизація та узагальнення розв’язування відомих уже рівнянь. Вводяться поняття “лінійне рівняння” та “рівняння першого степеня”, проводиться дослідження коренів лінійного рівняння ax=b залежно від коефіцієнта а і вільного члена b. Учні розв’язують текстові задачі за допомогою лінійних рівнянь. Далі такі рівняння розв’язуються у зв’язку з вивченням тотожних перетворень цілих виразів та їх застосуванням.
Вивчаючи дію множення одночлена на многочлен, та під час розкладання многочленів на множники з’являються неповні квадратні рівняння.
Розв’язують рівняння, до складу яких входять дроби, знаменники яких є числа, і після перетворень зводяться до лінійних.
На завершення курсу алгебри 7-го класу, вводиться поняття про лінійне рівняння з двома змінними, його графік, систему лінійних рівнянь з двома змінними та способи їх розв’язання.
Теоретичний матеріал цього пункту закріплюється під час виконання вправ.
Звертається увага учнів на те, що при а 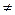 0, рівняння ax=b називається рівнянням першого степеня з однією змінною, яке має єдиний корінь х=
0, рівняння ax=b називається рівнянням першого степеня з однією змінною, яке має єдиний корінь х= 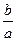 .
.
Лінійне рівняння ax=b може мати:
а) єдиний корінь, при а 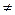 0;
0;
б) зовсім не має коренів, при а=0;
в) безліч коренів, при а=0 і b=0.
На закріплення пропонуються вправи: які з наведених нижче рівнянь є лінійними, а які – першого степеня?
а) –2х=12;
б) 8у=0;
в) 0z=10;
г) 0х=0.
Розглядаються приклади рівнянь, що не мають або мають безліч розв’язків.
Для учнів з високим рівнем навичок можна запропонувати вправи творчого характеру.
Наприклад: розв’яжіть рівняння
1) ах=5;
2) 5х=а;
3) (а-1)х=7;
4) (с2+2)х=b.
Особливо труднощі викликають рівняння х+х=0, 5у-6у=0. Пропонуються усні вправи: підберіть значення а, при якому рівняння ax=0 має: а) єдиний корінь; б) безліч коренів.
Після розв’язування конкретних рівнянь, які зводяться до лінійних треба зробити загальний висновок (скласти схему розв’язання):
1. звільнитись від знаменників (якщо вони є);
2. розкрити дужки (якщо вони є);
3. перенести члени із змінними в одну частину, а інші в другу;
4. звести подібні доданки, тобто звести рівняння до виду ax=b;
5. знайти х і записати відповідь.
Дається взірець оформлення розв’язання:
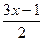 -
- 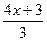 =
= 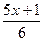 /
/  6;
6;
3(3х-1)-2(4х+3)=5х+1;
9х-3-8х-6=1+3+6;
-4х=10;
х=- 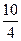 =-
=- 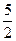 =-2,5.
=-2,5.
Відповідь: х=2,5.
Для виховання навичок самоконтролю корисно іноді пропонувати учням виконувати перевірку.
