Функциональная привязанность и трафаретное мышление
Вспомните рассмотренную выше задачу о двух веревках. Цель состояла в том, чтобы одновременно ухватить концы обеих веревок, свешивающихся с потолка. Правильное решение заключалось в раскачивании одной из веревок с предварительно привязанным к ее концу грузом — например, плоскогубцами. Одной из причин, по которой эта задача кажется очень сложной, является функциональная привязанность. Человек настроен или «привязан» к обычному использованию плоскогубцев, и ему трудно осознать, что их можно использовать не по прямому назначению. Другой пример функциональной привязанности был упомянут во введении (глава 1). В классической задаче со свечой тестируемым было предложено прикрепить свечу к стене, чтобы она могла гореть, используя при этом лишь коробок с кнопками и несколько спичек. У людей, которым была предложена эта задача, возникали трудности с представлением коробка в качестве подсвечника, поскольку они воспринимали его как упаковку для спичек или кнопок, т. е. рассматривали только прямое функциональное назначение коробка. (439:)
Функциональная привязанность — это один из видов трафаретного мышления. Я рассматриваю эти понятия как «привычные способы мышления» человека. Они заранее определяют пути развития мысли и реакции человека. Чтобы продемонстрировать, насколько мощным может оказаться трафаретное мышление, рассмотрим задачу о девяти точках, приведенную на рис. 9.18. Отложите на время дальнейшее чтение и попытаетесь ее решить.

Рис. 9.18. Задача о девяти точках. Соедините все девять точек, проведя не более четырех прямых линий и не отрывая карандаш от бумаги.
Трудность решения этой задачи вытекает из автоматически воспринимаемого строгого расположения этих точек в форме квадрата. Большинство людей пытаются решить эту задачу, оставаясь в рамках воображаемого квадрата, образованного точками по внешней границе. Если вы продлите линии за границы воображаемого квадрата, то обнаружите довольно простое решение задачи. Кроме того, большинство людей полагает, что линии должны проходить через центры точек. Одно из решений задачи о девяти точках показано на рис. 9.19.
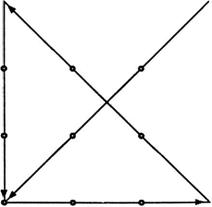
Рис. 9.19.Одно из возможных решений задачи о девяти точках.
Заметьте, что решение подразумевает нестандартный путь Большинство людей полагает, что линии должны оставаться в границах квадрата и проходить через центры точек
Но есть еще несколько решений этой задачи. Каждое из них предполагает уход от трафаретного мышления. Два решения представлены на рис. 9.20. Другие, более экзотические решения, среди которых предложение одной десятилетней девочки провести через все девять точек одну жирную прямую, можно найти в чудесной
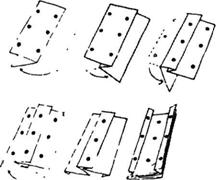
Другое возможное решение сложите бумагу с точками, как показано на рисунке, и точки выстроятся в одну прямую линию
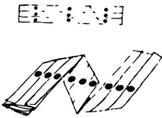
Можно также свернуть бумагу с точками в рулон и прочертить спиральную линию через точки, перейдя, таким образом, от плоскостной задачи к пространственной
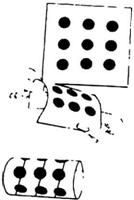
Рис. 9.20.Другие возможные способы решения задачи о девяти точках (Источник: Adams, 1979)
книге Дж. Л. Адамса (Adams, 1979) «Раскрепощение мысли». Желание остаться внутри квадрата слишком сильно, и его трудно преодолеть. Стратегии, которые позволяют вам увидеть задачу в новых ракурсах, например стратегия личной аналогии, одновременно способствуют поиску нетрадиционных путей решения.
