Методы проверки и подтверждения гипотез

В научном исследовании смелость в выдвижении гипотез должна сочетаться с тщательностью и строгостью их проверки. Обсуждая критерий проверяемости, мы уже отметили ряд трудностей, которые встречаются при испытании гипотез. Здесь мы коснемся более подробно некоторых проблем, связанных с проверкой и подтверждением гипотез.

4.6.1. Проблема проверки гипотез

Эмпирическая проверка гипотез в конечном итоге сводится к проверке тех следствий, которые из них вытекают, непосредственно с помощью результатов наблюдений или специально поставленных экспериментов. Такие следствия обычно выражаются в форме условных утверждений, т.е. утверждений, в которых перечисляются те требования, выполнение которых необходимо для появления того или иного события.

Если предсказания, выведенные из гипотезы, согласуются с данными наблюдения или эксперимента, то говорят, что гипотеза подтверждается этими данными.

В точных естественных науках, таких, как физика, астрономия, химия, результаты проверки гипотезы могут быть выражены количественным способом, чаще всего с помощью математических функций. Так, гипотеза о постоянстве ускорения всех свободно падающих тел была проверена с помощью логически выведенного из нее следствия о функциональной зависимости между временем падения тела и расстоянием, пройденным им за это время, т.е.

.

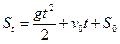Зная начальную скорость v₀ и положение тела S₀ к началу падения, мы можем непосредственно на опыте вычислить расстояние S_t, пройденное им за одну, две, три и т.д. секунды, и сравнить эти значения с теми, которые получаются из вышеприведенной формулы. Совпадение этих значений будет свидетельствовать о подтверждении эмпирически проверяемого следствия, а значит, и самой гипотезы, из которой оно выведено.

Но такое подтверждение зависит от числа проверенных случаев: чем больше значений для времени и расстояния S_t мы проверим, тем вероятнее будет наше заключение.

В строгом смысле слова, окончательная проверка следствия, как показывает формула, требует сопоставления бесчисленного множества значений для t и S_t. На опыте мы можем, разумеется, проверить лишь сравнительно небольшое конечное количество случаев. Поэтому в принципе всегда остается возможность опровержения гипотезы с помощью новых наблюдений и экспериментов.

Вот почему гипотезы общего характера никогда нельзя окончательно верифицировать на опыте.

С другой стороны, одного случая, не подтверждающего гипотезу, достаточно, чтобы опровергнуть ее целиком. Между подтверждением и опровержением гипотезы, как мы уже знаем, не существует симметрии. Именно основываясь на такой антисимметрии, К. Поппер и выдвинул свой критерий опровержения, или фальсификации, с помощью которого он предлагает отличать научные гипотезы и теории от ненаучных. Однако критерий опровержения нельзя противопоставлять критерию подтверждения, в особенности в науке.

Все предшествующие рассуждения об антисимметрии между подтверждением и опровержением гипотез основывались на тех формально-логических принципах, которые связаны с этими критериями. Из истинности следствия некоторого высказывания мы не можем заключать об истинности самого высказывания: это было бы логической ошибкой. Наоборот, ложность следствия свидетельствует о ложности высказывания, из которого оно вытекает. Такое умозаключение является логически правильным, известным в формальной логике под названием modus tollens. Когда эти принципы логики применяются для проверки отдельных, не связанных друг с другом гипотез, то настаивание на существовании асимметрии между подтверждением и опровержением не только допустимо, но и необходимо. Совершенно иначе обстоит дело, когда мы обращаемся к реальной практике науки, в которой одни гипотезы зависят от других, а также различных вспомогательных предположений.

В этом случае мы уже не можем так безапелляционно говорить об опровержении, как говорили об опровержении отдельной, изолированной гипотезы. Так, уже в случае проверки гипотезы о постоянстве ускорения свободно падающих тел наряду с самой гипотезой нам приходится считаться с такими вспомогательными предположениями или гипотезами, как отсутствие сопротивления воздуха, близость тела к земной поверхности и некоторые другие. Поэтому, если при проверке гипотезы окажется, что ее следствия будут противоречить данным опыта, то это, в строгом смысле слова, не будет свидетельствовать об окончательном опровержении исходной гипотезы. Вполне допустимо, что отрицательный результат опыта зависит от ложности какого-либо вспомогательного предположения, с которым связана исходная гипотеза. Все это говорит о том, что процесс проверки и опровержения гипотез, входящих в состав какой-либо научной теории, носит более сложный характер, чем это кажется на первый взгляд.

Если результат проверки некоторой основной и вспомогательных гипотез оказывается отрицательным, то точными логико-математическими средствами можно доказать, что в этом случае ложна либо основная гипотеза, либо одна или несколько, или даже все вспомогательные гипотезы. Установить это можно только в процессе дальнейшего исследования.

Указанные выше соображения имеют существенное значение для оценки роли так называемого решающего эксперимента. В науке нередко приходится иметь дело с конкурирующими гипотезами, которые опираются на одни и те же эмпирические данные и объясняют одни и те же явления. В таком случае, если бы нам удалось осуществить эксперимент, результаты которого опровергали одну из гипотез, другая из них могла претендовать на истинность. Но, как уже отмечалось, каждая из достаточно глубоких научных гипотез обычно связана с целым рядом вспомогательных предположений или гипотез. Поэтому отрицательный результат эксперимента может свидетельствовать не о ложности самой исходной гипотезы, а какого-либо вспомогательного предположения.

Если нам удастся исправить или модифицировать ошибочное вспомогательное предположение, то эксперимент может подтвердить основную гипотезу. Это означает, что эксперимент, окончательно опровергающий одну из конкурирующих гипотез и подтверждающий другую, осуществить крайне трудно, если не невозможно.

Другими славами, неоспоримое экспериментальное доказательство, то, что Ф. Бэкон называет Experimentum cruris, в науке фактически не встречается. По отношению к физике такой вывод о невозможности решающего эксперимента настойчиво защищался Пьером Дюгемом, а впоследствии в более общей форме эта идея развивалась У. Куайном.

В своей книге, посвященной структуре физической теории, Дюгем писал: «...физик никогда не может подвергнуть контролю опыта одну какую-нибудь гипотезу в отдельности, а всегда только целую группу гипотез. Когда же опыт его оказывается в противоречии с предсказаниями, то он может отсюда сделать лишь один вывод, а именно, что, по меньшей мере, одна из этих гипотез неприемлема и должна быть видоизменена, но он отсюда не может еще заключить, какая именно гипотеза не верна».

Справедливость своего тезиса Дюгем иллюстрирует на примере двух конкурирующих гипотез оптики: корпускулярной, или эмиссионной, гипотезы Ньютона и волновой гипотезы Гюйгенса и Френеля. Согласно первой гипотезе, свет представляет поток частиц, или корпускул, испускаемых светящимся телом. Волновая гипотеза рассматривает его как колебательное движение особой субстанции, названной мировым эфиром. Обе эти гипотезы более или менее удовлетворительно объясняли явления распространения, отражения и преломления света.

Но из волновой гипотезы вытекало также следствие, что скорость света в воздухе должна быть больше, чем в воде, тогда как, согласно корпускулярной, наоборот, скорость в воздухе должна быть меньше, чем в воде.

В 1850г. французский физик Фуко осуществил эксперимент, подтвердивший, что скорость света в воздухе действительно больше, чем в воде. Эти результаты многие ученые рассматривали как решающее доказательство опровержения корпускулярной гипотезы и подтверждения волновой. Поскольку, однако, обе эти гипотезы зависят от целого ряда других вспомогательных гипотез, то отрицательный результат эксперимента сам по себе не свидетельствует о ложности корпускулярной гипотезы.

Вполне возможно, что ошибочной является какая-либо из вспомогательных гипотез. Во всяком случае, полученный результат требовал пересмотра и модификации всей совокупности предположений и гипотез, связанных с корпускулярной концепцией. И действительно, после того как А. Эйнштейн в 1905 году вместо старых представлений о корпускулах выдвинул гипотезу о квантах света, или фотонах, то в качестве доказательства ее справедливости он сослался на опыты Ленарда. Эти опыты опровергали представления классической волновой теории о непрерывном характере световой энергии, и поэтому Эйнштейн расценивал их «как второй решающий эксперимент» относительно природы света. Но опять-таки эксперимент не целиком опровергал волновую гипотезу и сам Эйнштейн стремился модифицировать ее так мало, как это было возможно.

Этот пример из истории науки ясно показывает, что полное опровержение, как и подтверждение гипотез, входящих в состав теорий и связанных многочисленными отношениями с другими гипотезами, в каждый данный период времени фактически невозможно. Поэтому невозможен и решающий эксперимент, о котором писал Ф. Бэкон, т.е. эксперимент, окончательно и полностью опровергающий одну гипотезу и подтверждающий другую, ей противоположную. В современной зарубежной литературе по методологии науки этот тезис настойчиво защищался И. Лакатошем в его исследованиях по (методологии научно-исследовательских программ. Поскольку гипотезы в науке, как правило, объединяются в рамках некоторой концепции или, как предпочитает говорить Лакатош, определенной исследовательской программы, то никакой реальный эксперимент не может сразу же отвергнуть такую программу. «Не существует никаких решающих экспериментов,—подчеркивает он,—по крайней мере, если под ними подразумевать эксперименты, которые тотчас же могут ниспровергнуть исследовательскую программу. Фактически, когда одна исследовательская программа терпит поражение и заменяется другой, мы можем — довольно непредусмотрительно — назвать эксперимент решающим, если он обеспечивает эффектное подтверждение для побеждающей программы и не подкрепляет отвергаемую (в том смысле, что новые результаты никогда не были «объяснены прогрессивно» — или вообще «объяснены» — в рамках отвергаемой программы». Многочисленные примеры из истории развития новейшей физики, которые анализирует Лакатош, достаточно убедительно Свидетельствуют об относительном характере экспериментов в науке.

4.6.2. Проблемы подтверждения и опровержения гипотез

При решении проблем подтверждения и опровержения гипотез необходимо учитывать, идет ли речь об отдельной, изолированной гипотезе или же о некоторой их системе.

Игнорирование этого обстоятельства и неконкретный подход к вопросу чаще всего и порождает крайние, односторонние попытки решения проблемы.

Как уже отмечалось, дедуктивисты вроде Поппера и его последователей единственно приемлемым методом проверки гипотез считают дедукцию. Сторонники индуктивизма все свое внимание обращают на индуктивные методы подтверждения. Такое противопоставление, во-первых, хотя и имеет известные основания, все же не учитывает той специфической роли, которую играют гипотезы в науке. Фактически в любой достаточно зрелой науке они выступают не обособленно, а в рамках теорий, т.е. системы взаимосвязанных гипотез. Во-вторых, в процессе научного исследования опровержение и подтверждение гипотез скорее дополняют, чем исключают друг друга. Поэтому мы не можем согласиться с мнением Поппера о том, что научные законы эмпирических теорий могут быть только опровергаемы, но не подтверждаемы.

Конечно, принципиальная возможность опровержения гипотезы или теории является важным критерием ее содержательности. Теория, которая может только подтверждаться, дает либо тривиальное, либо слишком схематическое объяснение исследуемых явлений. Возможность опровержения гипотезы, как справедливо замечает М. Бунге, есть признак ее научности. Но это условие, будучи необходимым, не является вместе с тем достаточным.

Чтобы обосновать гипотезу, мы должны по крайней мере на некоторых частных случаях убедиться в ее правильности. Частные случаи, подтверждающие гипотезу, будут свидетельствовать хотя бы о ее частичной истинности.

Проблема оценки степени подтверждения гипотез до настоящего времени остается дискуссионной. Точные методы такой оценки впервые попытались применить еще основоположники математической логики — Г.В. Лейбниц и Д. Буль, а после них Ч. Пирс, Д. Венн и П.С. Поредкий. Лейбниц даже мечтал о создании специальной логики, которая учитывала бы степени вероятности не только гипотез, но и любых высказываний вообще. Эта программная идея Лейбница нашла дальнейшее развитие в исследованиях английского ученого Д.М. Кейнса (1921г.). Ha современном уровне, с использованием методов логической семантики вероятностная логика разрабатывается в трудах Р. Карнапа, Дж. Кемени, Г. Леблана и других.

Вероятностная логика, которая пришла на смену старой .классической индуктивной логике Бэкона — Милля, совершенно по-новому ставит проблему индукции.

Если раньше задачу индуктивной логики видели в открытии и доказательстве новых научных истин, то впоследствии стало совершенно очевидным, что с помощью правил индукции Бэкона — Милля можно открывать лишь весьма простые истины. В настоящее время перед индуктивной логикой ставятся задача — не изобретать правила открытия новых научных истин, а находить объективные критерии подтверждения гипотез эмпирическими посылками и, если возможно, определить степень, с которой эти посылки подтверждают гипотезу.

Степень вероятности гипотезы существенным образом зависит от тех посылок, которые служат для ее подтверждения.

С изменением посылок, получением новой информации меняется и вероятность гипотезы. Что касается численной оценки вероятности гипотез, то здесь мнения ученых расходятся. Большинство из них склоняется к мысли, что возможна лишь сравнительная оценка степени подтверждения гипотез. Иными славами, гипотезы можно лишь сравнивать в терминах «больше подтверждается», «одинаково подтверждается» или «меньше подтверждается». Учитывая, что эмпирические данные, на которые опираются разные гипотезы, могут оказаться различными, даже такое сравнение не всегда осуществимо.

Другие исследователи, как, например, Р. Карнап и его последователи, верят в возможность построения вероятностной логики, с помощью которой можно охарактеризовать степень подтверждения точным числом.

По-видимому, все же наиболее перспективными являются попытки создания сравнительной вероятностной логики, на чем так настаивал более осторожный Кейнс.

Как бы ни расходились мнения относительно оценки степени вероятности гипотез, тем не менее совершенно ясно, что методы вероятностной логики приспособлены главным образом для анализа подтверждения отдельных, логически между собой не связанных гипотез. В реальной науке такого рода гипотезы встречаются только тогда, когда мы имеем дело с эмпирической проверкой той или иной теории, но даже здесь приходится учитывать взаимовлияние гипотез друг на друга. Действительно, если гипотеза H₁ влечет гипотезу H₂, тогда подтверждение последней служит косвенным свидетельством первой. Именно так связаны друг с другом гипотезы в рамках гипотетико-дедуктивной системы. Поэтому по подтверждению эмпирически проверяемых гипотез можно косвенно судить о подтверждении гипотез, которые нельзя проверить непосредственно на опыте. Примеры подобного рода мы уже обсуждали.

Кроме подтверждения логических следствий гипотезы косвенным свидетельством ее правильности , могут служить также случаи подтверждения так или иначе связанных с ней гипотез того же уровня общности. Вот почему степень подтверждения гипотезы, включенной в теоретическую систему, увеличивается в такой мере, что с ней не может сравниться степень вероятности любого числа частных случаев ее подтверждения.